高考数学复习第二学期月考试卷2008.3.17

　　　　　　　　  满分150分，考试时间120分钟

一、填空题（本大题共11小题，满分44分）

1．已知直线的斜率是－1，则它的倾斜角是　　　　　　　　　 .

2．已知集合,则中元素的个数是　 .

3．若复数是纯虚数，则实数a的值是　　　　  .

4．已知向量若∥，则x=　　　　 .

5．抛物线的焦点是曲线的对称中心，顶点为坐标原点，则此抛物线的方程是　　　　　　　  .

6．已知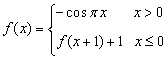，则的值等于　　　　　　　 .

7．函数的递增区间为____________________．

8. 实数满足，则取值范围是_____________．

9．已知函数为奇函数，函数为偶函数，且　　.

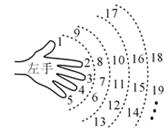10．在小时候，我们就用手指练习过数数. 一个小朋友按如图所示的规则练习数数，数到2008时对应的指头是　 　　 .(填出指头的名称，各指头的名称依次为大拇指、食指、中指、无名指、小指).

11．已知是等差数列的前n项和，且

，有下列四个命题：⑴；⑵；

⑶；⑷.其中正确命题的序号是 　　　　　　 ．

二、选择题（本大题共4小题，满分16分）

12. 已知p：则p是q的　　　　　　　　　　　　　　　  (　　)

A充分不必要条件　B必要不充分条件　　C充要条件　D既不充分也不必要条件

13. 在空间中，有如下命题：①互相平行的两条直线在同一平面内的射影必然是互相平行的两条直线；②若平面内任意一条直线m//平面，则平面//平面；③若平面与平面的交线为m，平面内的直线n⊥直线m，则直线n ⊥平面；④若点P到三角形三个顶点的距离相等，则点P在该三角形所在平面上的射影是该三角形的外心. 其中正确命题的个数为　　　　　　　　　　　　　  （　　）

　　　 A．1个　　　　 B．2个　　　　　　  C．3个　　 　　　 D．4个

14.篮球比赛进攻的一方由组织后卫把球传给其他四个队友中的任何一个,接着由拿球者再传给其他四人中的任何人,这样共传次,则第次球回到后卫手中传球的概率为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　).

　　A.　　　　  B.　　　　　　  C.　　　　　　 D.

15. 已知实系数一元二次方程的两根分别为，的取值范围是　　　 　　　　（　　）

　　　 A．　　　 B． 　　　C．　　　　D．

三、解答题

16．(本题满分12分) 已知函数求

　 （1）求的最小正周期；

　 （2）函数在区间上的最大值、最小值及相应的x值。

17．(本题满分14分) 如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，E是BC的中点，平面B₁ED交A₁D₁于F.

（1）指出F在A₁D₁上的位置，并说明理由；

（2）求直线A₁C与DE所成的角．

18．(本题满分14分) 彩虹灯具厂2006年生产节能灯10万只，每只销售价10元，每只固定成本5元.2007年工厂第一次投入10万元用于高科技开发，并计划以后每年比上一年多投入10万元.预计产量年递增1万只，第n次投入后，每只产品的固定成本g(n)=,若节能灯销售价保持不变，第n次投入后的年利利润为f(n)万元.

(1)求的值，并求f(n)的表达式；

(2)问从2007年算起第几年利润最高？最高为多少万元？

19．(本题满分16分) 已知函数 () ,

　　　 ⑴试确定的单调区间 , 并证明你的结论 ;

　　　 ⑵若时 , 不等式恒成立 , 求实数的取值范围

20．(本题满分16分) 在直角坐标平面中，△ABC的两个定点为A（0，－1），B（0，1），平面内两点G、M同时满足①（O为坐标原点），②，③。

　（1）求顶点C的轨迹E的方程；

　（2）直线l：与曲线E交于P，Q两点，求四边形PAQB的面积的最大值。

21．（本题满分18分）已知数列{a_n}的前n项为和S_n，点在直线上.数列{b_n}满足，前9项和为153.

　 （1）求数列{a_n}、{b_n}的通项公式；

　 （2）设，数列{c_n}的前n和为T_n，求使不等式对一切都成立的最大正整数k的值.

　 （3）设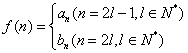，问是否存在，使得成立？若存在，求出m的值；若不存在，请说明理由.

高三数学月考答案

一、填空题： 1.　2．0　3．－6　4．2　5． 　6．3

7．（或或或）8．  9．－2

10．食指　11. ①②

二、选择题：12. A　13. B　14. C　15. D

三、解答题

16.解：（1）

∴函数的最小正周期………………6分

（2）令　　

上递减，

………………12分

17．解： （1）F为A₁D₁的中点

证明：由正方体ABCD—A₁B₁C₁D₁ 　面ABCD//面A₁B₁C₁D₁

面B₁EDF∩面ABCD=DE　面B₁EDF∩面A₁B₁C₁D₁=B₁F

∴B₁F//DE，同理：B₁E//DF　 ∴四边形DEB₁F为平行四边形

∴B₁F=DE，又A₁B₁=CD　 Rt△A₁B₁F≌Rt△CDE

∴A₁F=CE=　 ∴F为A₁D₁的中点　　　　　 …………7分

（2）过点C作CH//DE交AD的延长线于H，连结A₁H　 …………8分

则A₁C与DE所成的角就等于A₁C与CH所成的锐角即∠A₁CH（或其补角）

由于正方体的棱长为1，E为BC中点　　　　　　　　 …………9分

∴可求得A₁C=　在△A₁CH中，由余弦定理得：

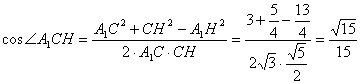　 …………13分

∴，即直线A₁C与DE所成的角为…14分

18．解：(1)由g(n)=，当n=0时，k=5　　　　　　　　 ……………2分

　f(n)=(10+n)（10-）—10n　　　　　　　　  　……………7分

 (2)f(n)=100－=100-5(+)≤100-5×2=70　…12分

当且仅当=，即n=8时取等号。

答：第8年工厂的利润最高，最高为70万元。　　　　　 ……………14分

19．解：（1）当时 , f(x)=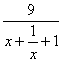, 　　　　　　　　 ------------2分

令g(x)=可得g(x)在区间上是减函数; 在区间上是增函数.　 5分

∴函数 ()在区间上是增函数; 在区间上是减函数 7分

（2）由（1）得,函数函数 ()在区间上是增函数 ,

　 ∴当时,  .-------12分

∵不等式恒成立 ,　∴ ,

解之得  .-----16分

20．解：（Ⅰ）设，由①知　 ∴

由②知M是△ABC的外心，∴M在x轴上，

由③知　　 …………4分

由 ，

∴动点C轨迹为椭圆，方程为　　…………7分

（Ⅱ）将

由　………………10分

设 ，

则

　 …………112分

∴　………………14分

∴t=0，四边形PAQB的面积的最大值　　………………16分

21、解：（1）由题意，得

故当时，

当n =1时，，而当n = 1时，n + 5 = 6，

所以， …………………………………………………… 2分

又，

所以{b_n}为等差数列，于是　　　　　　  …………4分

而

因此， ………………6分

　 （2）

 …………………………8分

　　　　  …………………………………………9分

由于，

因此T_n单调递增，故………………………………………………11分

令 …………………………………………12分

　 （3）

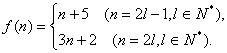
①当m为奇数时，m + 15为偶数.

此时，

所以 ………………………………………………14分

②当m为偶数时，m + 15为奇数.

此时，

所以（舍去）. ………………………………16分

综上，存在唯一正整数m =11，使得成立. …………………18分