函数综合训练（二）

一. 教学内容：

函数综合训练（二）

【模拟试题】（答题时间：120分钟）

一. 选择题：（每小题5分，共50分）

1. 函数，则的反函数的解析式为（　　）

A. 　　　　　　　　　B.

C. 　　　　 D.

2. 已知函数存在反函数，若，则函数的图象必经过点（　　）

　　A. 　 B. 　　C. 　　D.

3. 定义在R上的函数、都有反函数，又与的图象关于直线对称，若，则的值为（　　）

　　A. 2005　 B. 2006　 C. 2007　 D. 2008

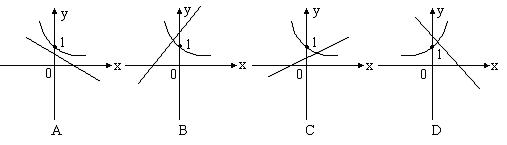
4. 当时，函数与的图象只可能是下图中的（　　）

5. 已知实数、满足，有下列5个关系式：

（1）；（2）；（3）；（4）；（5）其中不可能成立的有（　　）

A. 1个　　B. 2个　　C. 3个　　D. 4个

6. 已知的定义域是R，且为奇函数，当时，，那么的值是（　　）

　　A. 　　B. 2　　C. 　　D.

7. 若，则的取值范围是（　　）

　 A.（0，1）　 B. 　　C. 　　D.

8. 若对于，不等式（，且）恒成立，则的取值范围是（　　）

　　A. 　　B. 　　C. 　　D.（0，1）

9. 方程的实数解的个数是（　　）

　　A. 0　　B. 1　　C. 2　　D. 3

10. 设是定义在R上的偶函数，且对都有，在上，，那么在上，的反函数可以表示为（　　）

A. 　　　　　　　　　 B.

C. 　　　　　　 D.

二. 填空题：（每小题4分，共24分）

11. 函数（，且）在上的最大值比最小值大，则的值是　

　　 。

12. 实数、、的大小顺序是　　　　　　 。（用“”连接）。

13. 设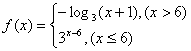的反函数为，若，则

　　　　。

14. 已知函数且，则　　　 。

15. 已知函数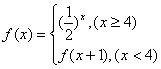，则的值是　　　。

16. 定义在R上的偶函数满足，且在上是增函数，给出下列命题：

① 是周期函数；② 的图象关于直线对称；③ 在上是增函数；④ 在[1，2]上是减函数；⑤

其中正确命题的序号是　　　　  。

三. 解答题：（共76分）

17. 求函数的反函数。（满分12分）

18. 解不等式：。（满分12分）

19. 设，其中，如果当时，有意义，求的取值范围。（满分12分）

20. 已知函数

（1）求的反函数；

（2）如果不等式对上的每一个的值都成立，求实数的取值范围。

  21. 已知在区间上是增函数。

（1）求实数的值组成的集合A；

（2）设关于的方程的两个非零实根为、。试问：是否，使得不等式对及恒成立？若存在，求的取值范围；若不存在，请说明理由。（满分14分）

  22. 函数是的反函数，的图象与函数的图象关于直线成轴对称图形，记。

（1）求的解析式及其定义域；

（2）试问的图象上是否存在两个不同的点A、B，使直线AB恰好与轴垂直？若存在，求出A、B的坐标；若不存在，说明理由。（满分14分）

【试题答案】

一.

1. B　　2. B　　3. C　　4. C　　5. B　　6. B　　7. C　　8. B　　9. C　　10. D

二.

11. 或　　12. 　　13. 　　14. 18　　15.

16. ①②⑤

三.

17.

解：当时，　 　 

　　∴ 此时

当时，　

∴ 此时

∴

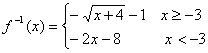
18.

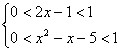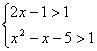
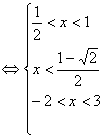解：或或

或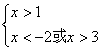　 ∴ 原不等式的解集为（3，）

19. 解：∵ 当时，有意义　

　　∴ 　　恒成立

即恒成立

设　　 则在上

∴ 　∴

  20. 解：

（1）（）　　

在上且

在上，且

∴ （）的值域为（0，1）

∵ 　 ∴ 　

∵ 　 ∴ 　

∴ 　 ∴

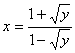（2）∵ 对恒成立

∴

即对恒成立

设　

∴

∴

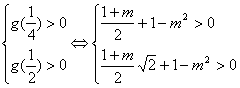
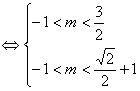
21. 解：

（1）∵ 　　

∴

∵ 在上　 ∴ 对恒成立

即，恒有成立

设　 ∴

（2）　　

∵ 　∴ 、是方程的两不等实根，且，

∴

∵ 对及恒成立

∴ 对恒成立

设，

∴ 对恒成立

∴

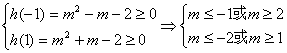
∴ 满足题意

22. 解：

（1）　 　 　 

∴ 　 

∵ 的图象与的图象关于直线成轴对称图形

∴ 的图象与的图象关于直线对称

即：是的反函数　

　　　∴ 　　∴

∴

（2）假设在的图象上存在不同的两点A、B使得轴

即使得方程有两不等实根

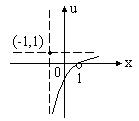
设，则在（，1）上且

∴ ，　 ∴ 使得方程有两不等正根

设，

由函数图象可知：，方程仅有唯一正根

∴ 不点A、B符合题意。