08级高考文科数学学生学业质量调研抽测试卷（第一次）
数学(文科)试题
本试题分I卷（选择题）和第II卷（非选择题）两部分。共150分，考试时间120分钟.
第I卷（选择题，共60分）
注意事项：
1．答题前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题上。
3．考试结束，监考人将本试题和答题卡一并收回.
一、选择题：（本大题共12个小题，每小题5分，共60分）.
1．集合A={1，2}的真子集的个数是 （ ）
A．1 B．2 C．3 D．4
2．抛物线
的焦点到准线的距离为 （
）
A．2 B．
C．4 D．8
3．若
，则x的值为 （
）
A．－2 B．
C．
D．2
4．设
那么“
”是“
”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
5．若函数
和函数
都是定义在实数集R上的函数，且方程
有实数解，则
不可能是 （ ）
A．
B．
C．
D．
6．已知数列{an}为等差数列，Sn为其前n项和，且
，则数列{an}的通项公式an为（ ）
A．n B．n+2 C．2n－1 D．2n+1
7．要得到函数
的图象，只需将指数函数
的图象 （ ）
A．向左平行移动个单位 B．向右科行移动个单位
C．向左平行移动
个单位 D．向右平行移动个单位
8．在对数式
中，实数a的取值范围是 （ ）
A．（2，3） B．（2，3）∪（3，6）
C．（2，6） D．（2，4）∪（4，6）
|
的部分图象如图所示，
则
的值为
（ ）
A．－2 B．2
C．－
D．
10．过椭圆：
的左焦点作直线
轴，交椭圆C于A、B两点. 若△OAB（O为坐标原点）是直角三角形，则椭圆C的离心率e为 （ ）
A．
B．
C．
D．
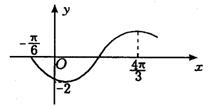
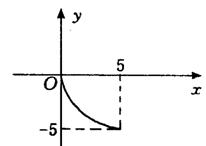
11．若函数
的图象是如图所示的一个四分之一的圆弧，则函数
是（ ）
|
B．
C．
D．
12．若直线
、N两点，且M、N两点关于直线
对称，则不等式组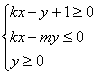
表示的平面区域的面积是 （ ）
A． B． C．1 D．2
第Ⅱ卷（非选择题，共90分）
二、填空题：（本大题4个小题，每小题4分，共16分）
13．已知函数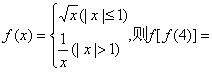
.
14．某种品牌的洗衣机在洗涤衣物时每清洗一次可清除掉衣物上此次清洗之前污渍的80%，若要使衣物上残留污渍不超过原有污渍的1%，则至少要清洗 次.
15．已知△ABC的三个内角A、B、C满足
=
.
16．已知
的最大值为
.
三、解答题：（本大题6个 小题，共74分）（必须写出必要的文字说明、演算步骤或推理过程）
17．（13分）解关于x的不等式
R）.
18．（13分）已知函数
的周期为2
.
（I）当
时，求y的取值范围；
（II）求该函数的单调减区间及对称轴方程.
19．（12分）已知数列{
}的前n项和为
平行.
（I）证明：
是等比数列；
（II）求an与Sn的通项公式.
20．（12分）进入2007年以来，猪肉价格上涨，养猪所得利润比原来有所增加. 某养殖户拟建一座平面图（如图所示）是矩形且面积为200平方米的猪舍养殖生猪，由于地形限制，猪舍的宽x不少于5米，不多于a米，如果该养殖户修建猪舍的地基平均每平方米需投入10元，房顶（房顶与地面形状相同）每平方米需投入15元，猪舍外面的四周墙壁每米需投入20元，中间四条隔墙每米需投入10元. 问：当猪舍的宽x定为多少时，该养殖户投入的资金最少，最少是多少元？
 |
x
|
的左支交于点A，与右支交于点B.
（I）求实数k的取值范围；
（II）若以AB为直径的圆过坐标的点O，求该圆的方程.
22．（12分）设函数的定义域为R，当
，且对任意的实数x，y∈R，
有
.
（I）求f（0），判断并证明函数的单调性；
（II）数列
N*）.
（1）求数列
的通项公式；
（2）当
对于n不少于2的正整数恒成立，求x的取值范围.
08级高考文科数学学生学业质量调研抽测试卷（第一次）
数学(文科)试题参考答案
一、选择题（本大题12个小题，每小题5分，共60分）
CCDADC， CBBACA
二、填空题（本大题4个小题，每小题4分，共16分）
13． 14．3 15．
16．
三、解答题（本大题6个 小题，共76分）
17．（13分）
解：由
………………（3分）
（1）当a<1时，解得a<x<1;
（2）当a=1时，解集为
；
（3）当a>1时，解得1<x<a. ………………（12分）
综上所述，当a<1时，原不等式的解集为
时，原不等式的解集为；
当a<1时，原不等式的解集为
………………（13分）
18．（13分）
解：
………………（3分）
∴函数
………………（4分）
（I）若
∴y的取值范围为
.
………………（7分）
（II）由
Z）得
∈Z），
∴原函数的单减区间为
Z）.…………（10分）
又由
Z），
∴原函数的对称轴方程为
Z）.
………………（13分）
19．（12分）
解：（I）由
平行，得1
即
……①
………………（2分）
……②
∴将①②相减得
………………（6分）
是等比数列.…………（8分）
（II）由（I）得
. ………………（10分）
………………（12分）
20．（12分）
解：设该养殖户投入资金为y元，则猪舍的长为
米，
………………（6分）
∵函数
上递增，
此时x=a. ………………（11分）
答：若a≥10米时，猪舍的宽定为10米，该养殖户投入的资金最少是6600元；
若
米时，猪舍的宽就定为a米，该养殖户投入的资金最少是
元.
………………（12分）
21．（12分）
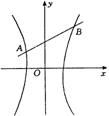
解：（I）由图观察知，直线l的斜率应介于双曲线的两渐近线的斜率之间，而两渐近线的斜率为
，所以
.
………………（4分）
（II）设
又A，B两点在直线l上，所以
代入上式有
……① ………………（6分）
又∵A，B两点为直线l与双曲线C的交点，
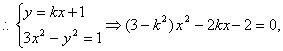……②
代入①中解得k=±1，即直线l的方程为
………………（8分）
∴所求圆的圆心为AB的中点
，
而半径为
∴所求圆的方程为
………………（12分）
22．（12分）
解：（I）令
………………（1分）
………………3分
任取
上是减函数.
………………（6分）
（II）（1）
∴的单调性得
是公差为2的等差数列，
………………（8分）
（2）记
，
是递增数列.
………………（10分）
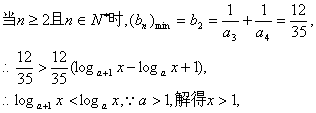
故x的取值范围是
………………（12分）