高中学生学科素质训练
高三数学测试题—立体几何综合测试(12)
一、选择题(本题1—10题每小题4分,11—14小题每小题5分,共60分)
1.在空间四边形ABCD各边上分别取E、F、G、H四点,如果EF与GH能相交于点P,那
么 ( )
A.点P必在直线AC上 B.点P必在直线BD上
C.点P必在平面ABC内 D.点P必在平面ABC外
2.给出直线a、b,平面α、β,点A,那么下面的说法中正确的是 ( )
|
|
B.若a⊥b,则a∩b=A
|
|
3.α、β表示平面,l表示既不在α内也不在β内的直线,存在以下三个事实①l⊥α;
②l∥β;③α⊥β.若以其中两个为条件,另一个为结论,构成命题,其中正确命题的个
数为 ( )
A.0个 B.1个 C.2个 D.3个
4.M,N,P表示三个不同的平面,则下列命题中,正确的是 ( )
A.若M⊥P,N⊥P,则M∥N
B.若M⊥N,N∩P=φ,则M∩P=φ
C.若M、N、P两两相交,则有三条交线
D.若N∩P=a,P∩M=b,M⊥N,则a⊥b
5.一条长为60的线段夹在互相垂直的两个平面之间,它和这两个平面所成的角分别为
45°和30°,这条线段的两个端点向平面的交线引垂线,则垂足间的距离是 ( )
A.30 B.20 C.15 D.12
6.空间三条射线PA,PB,PC满足∠APC=∠APB=60°,∠BPC=90°,则二面角B-PA-C
的度数 ( )
A.等于90°
B.是小于120°的钝角
C.是大于等于120°小于等于135°的钝角
D.是大于135°小于等于150°的钝角
7.三棱锥的三条侧棱两两垂直,其长分别为1、![]() 、
、![]() ,则此三棱锥的外接球面积为( )
,则此三棱锥的外接球面积为( )
A.6π B.12π C.18π D.24π
8.半径为1的球面上有A、B、C三点,A与B、A与C之间的球面距离都是![]() ,B和C之
,B和C之
间的球面距离为![]() ,则过A、B、C三点的截面与球心的距离是 ( )
,则过A、B、C三点的截面与球心的距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.a,b,c表示直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;
|
其中正确命题的个数有 ( )
A.0个 B.1个 C.2个 D.3个
10.设正四棱锥S—ABCD的侧棱长为![]() ,底面边长为
,底面边长为![]() ,E是SA的中点,则异面直线
,E是SA的中点,则异面直线
BE与SC所成的角是 ( )
A.30° B.45° C.60° D.90°
11.在三棱锥A—BCD中,AB=AC=AD,BC=1,∠ABC=∠BCD,∠BDC=![]() ,∠ABD=
,∠ABD=![]() ,
,
|
A.1 B.![]() C.
C.![]() D.
D.![]()
12.直三棱柱ABC—A1B1C1的体积为V,点P、Q分别在侧棱AA1和
CC1上如图,AP=C1Q,则四棱锥B—APQC的体积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.已知二面角α—AB—β的平面角是锐角θ,α内一点C到β的距离为3,点C到棱AB
的距离为4,那么tanθ的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.ABCD—A1B1C1D1是正方体,M、N分别是AA1、BB1的中点,设C1M与DN所成的角
为θ,则sinθ的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本题每小题5分,共20分)
15.在△ABC中,BC=21,∠BAC=120°,△ABC所在平面外一点P到A、B、C的距离都
是14,则P到平面ABC的距离为 .
16.在△ABC中,∠ABC=90°,AB=BC=a,BD⊥AC于D,以BD为棱折成直二面角A—
BD—C,P是AB上的一点,若二面角P—CD—B为60°,则AP= .
17.已知三棱锥A—BCD的体积是V,棱BC的长是a,面ABC和面DBC的面积分别是S1
和S2,设面ABC和面DBC所成的二面角是α,则sinα= .
18.正方体ABCD—A1B1C1D1中,O是上底面ABCD中心,若棱长为a,则三棱锥O—AB1D1
的体积为 .
三、解答题(本题19题10分,20—24小题每小题12分,共70分)
19.已知P、Q、M分别是45°的二面角α—l—β的面α、β和棱l上的点,直线MQ是直
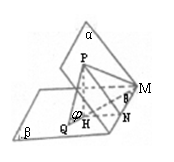 线PQ在β上的射影(如图),若PQ和β成
线PQ在β上的射影(如图),若PQ和β成![]() 角,l和MQ成θ角,PM=a,求PQ的长.
角,l和MQ成θ角,PM=a,求PQ的长.
|
20.已知二面角α—l—β等于θ,PA⊥α,PB⊥β,A、B为垂足,若PA=m,PB=n,求P
到棱l的距离.
21.A是△BCD所在平面外的点,∠BAC=∠CAB=∠DAB=60°,AB=3,AC=AD=2.
(Ⅰ)求证:AB⊥CD;
(Ⅱ)求AB与平面BCD所成角的余弦值.
22.正三棱柱ABC—A′B′C′中,AA1=2AB,D、E分别是侧棱BB1、CC1上的点,且
EC=BC=2BD,过A、D、E作一截面,求:
(Ⅰ)截面与底面所成的角;
(Ⅱ)截面将三棱柱分成两部分的体积之比.
23.经过正三棱柱底面一边AB作与底面成30°角的平面,已知截面三角形ABD的面积为
32cm2,求截面截得的三棱锥D—ABC的体积.
|
射影O在AC上.
(Ⅰ)求AB与侧面AC1所成的角;
(Ⅱ)若O恰是AC的中点,求此三棱柱的侧面积.
高三数学测试题参考答
十二、立体几何综合测试
一、(1)A;(2)D;(3)C提示:由①②![]() ③、①③
③、①③![]() ②是正确命题,由②③不能得到①;(4)B;
②是正确命题,由②③不能得到①;(4)B;
(5)A;(6)B;(7)A 提示:外接球的直径是以三条侧棱构成的长方体的对角线的长; (8)A;
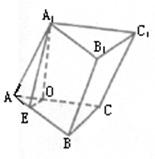
(9)B;(10)C 提示:连AC、BD交于O,连OE,则OE//SC.
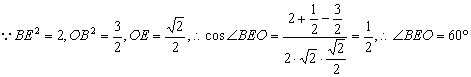 ;
;
(11)C;由已知条件知A点在底面BCD上的射影为BC的中点F,设∠ABC=∠BCD=α,则BD=a,
AB=sinα,![]()
(12)B;提示:取P、Q分别为AA1、CC1的中点,设矩形AA1C1C的面积为S,点B到底面AA1C1C
的距离为h,则 ![]()
(13)D; (14)D.
二、(15)7; (16)![]() ; (17)
; (17)![]() ; (18)
; (18)![]() .
.
三、(19)作PH⊥β于H,∵MQ是PQ在β上的射影,∴H在MQ上.作HN⊥l于N,并连结PN,由三垂
直线定理可知PN⊥l, ∴∠PNH是二面角α—l—β的平面角,即∠PNH=45°.
设PQ=x,则NH=PH=xsin![]() ,
,![]() ,MN=NH·cotθ=xsin
,MN=NH·cotθ=xsin![]() ·cotθ.
·cotθ.
在Rt△PMN中,∵PM2=PN2+MN2,![]() ,故
,故![]() .
.
|
|
∵l⊥AC,l⊥PC,l⊥BC, ∴PACB是一个平面四边形. 又∠PAC=∠PBC=90°,∴四边形PACB内
接于以PC为直径的圆,∠APB=π-θ. 在△APB中,由余弦定理,得 AB2=PA2+PB2-2PA·PBcos
∠APB=m2+n2+2mncosθ. 由正弦定理,得![]() ,即为所求P到
,即为所求P到
l的距离.
(21)(Ⅰ)∵∠BAC=∠CAD=∠DAB=60°, AC=AD=2,AB=3, ∴△ABC≌△ABD,BC=BD.
取CD的中点M,连AM、BM,则CD⊥AM,CD⊥BM. ∴CD⊥平面ABM,于是AB⊥BD.
(Ⅱ)由CD⊥平面ABM,则平面ABM⊥平面BCD,这样∠ABM是AB与平面BCD所成的角.
在△ABC中,AB=3,AC=2,∠BAC=60°,![]() . 在△ACD中,
. 在△ACD中,
AC=AD=2,∠CAD=60°,∴△ACD是正三角形,AM=![]() . 在Rt△BCM中,BC=
. 在Rt△BCM中,BC=![]() ,CM=1,
,CM=1,
![]() .
.![]()
(22)(Ⅰ)延长ED交CB延长线于F,![]()
![]() 为截
为截
面与底面所成二面角的平面角. 在Rt△AEC中,EC=AC,故得∠EAC=45°.
(Ⅱ)设AB=a,则![]() ,
,
![]() .
. 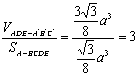
(23)S底面=S△ABD·cos30°,设底面边长为x,则有![]() .取AB中点E,在Rt△DEC中,
.取AB中点E,在Rt△DEC中,
∠DEC=30°,故![]()
(24)(Ⅰ)在△ABC中,AB=![]() ,BC=AC=a,∴△ABC是等腰直角三角形,BC⊥AC,∠CAB=45°,
,BC=AC=a,∴△ABC是等腰直角三角形,BC⊥AC,∠CAB=45°,
又BC⊥A1O,故BC⊥侧面AC1,AB与侧面AC1所成角就是∠BAC=45°.
(Ⅱ)由(Ⅰ)知四边形B1BCC1为矩形,![]() 中点,
中点,
![]() 于E,连结A1E,则AB⊥A1E. 在Rt△AOE
于E,连结A1E,则AB⊥A1E. 在Rt△AOE
中,![]() ,在Rt△A1EO中,
,在Rt△A1EO中,![]()
![]() .
.