圆锥曲线专题训练(2006年4月)
一、选择题(每小题5分，共50分)
1．方程
的两个根可分别作为（ ）
（A）一椭圆和一双曲线的离心率．（B）两抛物线的离心率．
（C）一椭圆和一抛物线的离心率．（D）两椭圆的离心率．
2．曲线
与曲线
(k<9)的（
）
（A）长、短轴相等． （B）焦距相等． （C）离心率相等． （D）准线相同．
3．双曲线
的两条准线的距离等于（ ）
（A）
． （B）
． （C）
． （D）
．
4．如果双曲线上一点P到双曲线右焦点的距离是8，那么点P到右准线的距离是（ ）
（A）
． （B）
． （C）
． （D）
．
5．准线方程为
的抛物线的标准方程是（ ）
（A）
． （B）
． （C）
． （D）．
6．已知双曲线
的焦点为F1和F2，点M在此双曲线上，且
，则点M到x轴的距离为（ ）
（A）
． （B）
． （C）
． （D）
．
7．若椭圆
的离心率为
，则实数m等于（ ）
（A）
或
． （B）． （C）
． （D）或
．
8.已知双曲线
的左支上有一点M到右焦点F1的距离为18，N是MF1的中点，O为坐标原点，则ON等于（ ）
（A）4． （B）2． （C）1． （D）．
9.直线y=
与双曲线
＞0,b＞0）的交点在实轴上的射影恰好为双曲线的焦点，则双曲线的离心率为
（A）
．
（B）2．
（C）2．
（D）4．
10．椭圆
的焦点是F1和F2，点P在椭圆上，且
是钝角，则
的面积的取值范围是（ ）
（A）
． （B）
． （C）
． （D）
．
二、填空题（每小题5分，共20分）
11．抛物线
的准线方程是y=2，则实数
的值为
。
12．抛物线
的焦点坐标为
；准线方程是
。
13．点P（0，2）到圆
的圆心的距离为 ，如果点A是圆C上的一个动点，AB的中点为P，那么点B的轨迹方程为
。
14．抛物线的准线为y轴，焦点运动的轨迹为y2-4x2+8y=0(y≠0)，则其顶点运动的轨迹方程为_______.
三、解答题
15. （本题满分12分）已知椭圆
上一点P到左右焦点的距离之比为2:3，求P到右准线的距离。
16. （本题满分12分）若双曲线的焦点到其渐近线的距离等于焦距的
倍，求双曲线的离心率。
17. （本题满分14分）
已知中心在原点的双曲线C的右焦点为（2，0），实轴长为2
.
（1）求双曲线C的方程；
（2）若直线l:y=kx+与双曲线C左支交于A、B两点，求k的取值范围；
（3） 在（2）的条件下，线段AB的垂直平分线l0与y轴交于M（0，b），求b的取值范围。
18．（本小题满分14分）
椭圆的短轴长为2，中心为原点O，对应于焦点F(c,
0) (c>0)的准线l与x轴相
交于点A，OA=3FA，过A的直线与椭圆交于P，Q两点。
（I）求椭圆的方程及离心率；
（II）若直线PQ的斜率为
，求△FPQ的面积。
19．（本小题满分14分）
给定抛物线C：，过点A（－1，0）斜率为k的直线与C相交于M，N两点。
（I）设线段MN的中点在直线x=3上，求k的值；
（II）设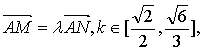
求
的取值范围。
20．(本小题满分14分)
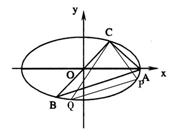
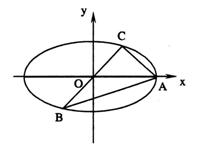已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个顶点，BC过椭圆中心O，如图，且
，BC=2AC.
（1） 求椭圆的方程；
（2） 如果椭圆上两点P、Q使∠PCQ的平分线垂直AO，则总存在实数λ，使
请给出证明.
参考答案
1-5 ABADD 6-10 CAABA
11．-8；
12．
，
；
13．
；
14. y2-16x2+8y=0(y≠0)；
15．（略）；
16．（略）；
17．（1）设双曲线方程为
(a＞0,b＞0),
由已知得a=,c=2,
再由a2+b2=c2, ∴b2=1.
∴双曲线方程为
(2)将y=kx+代入.
得(1-3k2)x2-6kx-9=0.
由题意知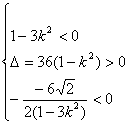
即
.
∴当时，l与双曲线左支有两个交点.
（3）设A（xA,yA），B（xB,yB）.
由（2）得xA+xB=
∴yA+yB=(kxA+
∴AB中点P的坐标为(
设l0方程为y=-
将P点坐标代入l0方程，得b=
由（2）知
∴b的取值范围是（－∞，－2）。
18．解（I）因为椭圆短轴长为
，所以
，由已知
……2分
解得
………………4分
所以椭圆方程为
………………6分
（II）由（I）知A（3，0），F（2，0），直线PQ的方程为
。
由方程组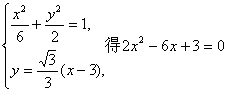
。
设
……①，
……②……………8分
, ………………9分
将①②代入得，PQ=2， ………………10分
F（2，0）到直线PQ：
，……13分
所以三角形△FPQ的面积为。 ………………14分
19．解（I）过点A（－1，0）斜率为k的直线为
，
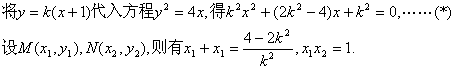
因为线段MN的中点在直线x=3上，所以
……3分
所以，
（此时（*）式的判别式大于零） ………………5分
（II）由题设
|
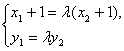………………7分
由②得
③
由①、③得
，…………9分
所以，
， ………………10分
因为
， ………………12分
注意到
， ………………14分
所以的取值范围是
。
20．(1)如图所示，易知点A坐标为（2，0），
设所求椭圆的方程为:
(0＜b＜2），
由椭圆的对称性知OC=OB，由得AC⊥BC.
∵BC=2AC,∴OC=AC.
∴△AOC是等腰直角三角形, ∴C的坐标为（1，1）.
∵C点在椭圆上，∴
∴b2=
所求的椭圆方程为
。
(2)由于∠PCQ的平分线垂直OA（即垂直于x轴），不妨设直线PC的斜率为k，则直线QC的斜率为-k,直线PC的方程为：y=k(x-1)+1,直线QC的方程为y=-k(x-1)+1,
由
得（1+3k2）x2-6k(k-1)x+3k2-6k-1=0(※)
∵点C（1，1）在椭圆上,∴x=1是方程(※)的一个根，则其另一根为
.
设P（xP,yP）,Q(xQ,yQ),则xP=，同时，xQ=
.
KPQ=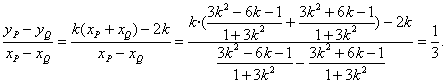
而由对称性知B（-1,-1），又A（2，0），∴
∴KPQ=KAB, ∴
，且
即存在实数λ，使