圆 锥 曲 线 单 元 测 试 题

四川省邻水中学(国家级示范高中) 特级教师 杨才荣 638500

一、选择题 (每小题3分，共36分) .

1、双曲线-=1的两条渐近线互相垂直，则此双曲线的离心率是　 (　　)

　　(A)　　　　 (B)2　　　　 (C)2　　　　 (D)翰林汇

2、方程mx²＋ny²＋mn=0 (m<n<0) 所表示的曲线的焦点坐标是　　　　　  (　　)

　　(A)　(0，)　　　　　　　　　　  (B)　(0，)

　　(C)　(，0)　　　　　　　　　　  (D)　(，0)翰林汇

3、椭圆与双曲线有公共焦点，P是椭圆与双曲线的交点，则PF₁·PF₂的值为　　　　　　　　　　　　　　  (　　)

(A)　a²＋m²　　　　　　　　　　　　　  (B)　b²－n²

(C)　a²－m² 或b²＋n²　　　　　　　　　 (D)　a²＋m² 或b²－n²翰林汇

4、设x²－y²=4，则的取值范围是　　　　　　　　　　　　　　  (　　)

(A)（－，0）∪（0，＋）　　　　　  (B)（－1，1）

(C)（－8，）　　　　　　　　　　　　  (D)（－，－2）∪[2，＋]翰林汇

5、设双曲线的左、右焦点是F₁、F₂，左、右顶点为M、N，若△PF₁F₂的顶点P在双曲线上,则△PF₁F₂的内切圆与边F₁F₂的切点位置　　　　　　　　　　　　　　　  (　　)

(A)不能确定　　　　　　　　　　　　　　  (B)在线段MN的内部

(C)在线段F₁M内部或在线段NF₂内部　　　　(D)是点M或点N翰林汇

6、方程表示双曲线的必要但非充分条件是　　(　　)

(A)＜k＜2　　　　　　　　　　　　　　　  (B)－3＜k＜－

(C) ＜k＜2 或－3＜k＜－　　　　　　　  (D)－3＜k＜2翰林汇

7、直线x－y－1=0与实轴在y轴上的双曲线x²－y²=m的交点在以原点为中心，边长为2且边平行于坐标轴的正方形内部，那么m的取值范围是　　　　　　　　　　 (　　)

(A) 0＜m＜1　　　 (B) m＞－1　　　　(C) m＜0　　　 (D) －1＜m＜0翰林汇

8、过点P(－3，－4)的直线与双曲线有一个公共点，则直线l的方程为　　 (　　)

(A) 4x－3y=0　　　　　　　　　　　　  (B) 4x＋3y＋24=0

(C) x＋3=0　　　　　　　　　　　　　  (D) x＋3=0或4x＋3y＋24=0翰林汇

9、双曲线的两条渐近线所夹的锐角是　　　　　　　　　　　 (　　)

(A) 　　　　　　　　　　　　 (B)

(C)　2　　　　　　　　　　　 (D) 翰林汇

10、过点A(1,1)作双曲线的弦MN，使A为MN的中点，则直线MN的方程是　　(　　)

(A) 2x－y－1=0　　　　　　　　　　　　  (B )x－2y＋1=0

(C) 2x＋y－3=0　　　　　　　　　　　　  (D) 不存在

翰林汇11、焦点在x轴上，实轴长为8，一条渐近线方程是3x－2y=0的双曲线的标准方程是　　(　　)

(A) 　　　　　　　　　　　　　 (B)

(C) 　　　　　　　　　　　　　 (D) 翰林汇

12、以椭圆的顶点为焦点、焦点为顶点的双曲线方程为　　　  (　　)

(A) 　　　　　　　　　　　　　 (B)  

(C) 　　　　　　　　　　　 (D) 翰林汇

二、填空题(每小题4分，共24分).

13、双曲线离心率为2，则渐近线夹角为________。翰林汇

14、若双曲线上的点A到一个焦点的距离为12，则点A到另一个焦点的距离为________，双曲线上符合上述条件的点A共有________个。

15翰林汇、直线y=x－1被双曲线2x²－y²=3所截得弦的中点坐标是________，弦长为________。翰林汇

16、曲线ax²＋y²＋1=0(－1＜a＜0＝的焦点坐标为________。翰林汇

17、经过点P（1，1）作直线l，若l与双曲线x²－y²=1有两个不同的公共点，则直线l的斜率k的取值范围是________。翰林汇

18、已知方程表示双曲线，则k的取值范围是________。翰林汇

三、解答题(每小题8分，共40分).

19、过双曲线的左焦点F₁作倾斜角为的直线与双曲线交于A，B两点，求AB.翰林汇

20、双曲线16x²－9y² = 144,F₁、F₂是左、右焦点，P在双曲线上，且，求F₁PF₂的大小。翰林汇

21、已知双曲线的中心在原点，以坐标轴为对称轴，且与圆x²＋y² = 17相交于点A（4，－1），若此圆在A点之切线与双曲线一条渐近线平行，求此双曲线方程。翰林汇

22、已知双曲线C：,F₁、F₂分别是它的左右焦点,抛物线l的焦点与C的右焦点重合,l的准线与C的左准线重合,P是C和l的一个交点. 求证：=1.翰林汇

23、点P在双曲线=1上,F₁、F₂为焦点,△PF₁F₂的内切圆切x轴于A点,如图,求证：A为双曲线的顶点.。

翰林汇

参考答卷

一、　1、A  翰林汇2、B　翰林汇3、C　翰林汇4、B　翰林汇5、D　翰林汇6、D　7、 D  翰林汇8、D　翰林汇9、 D　翰林汇10、D　翰林汇11、C　翰林汇12、B　翰林汇

二、　13、60⁰翰林汇　　　14、4或20 ，8　　　 翰15、(－1，－2)，翰林汇　　　 16、

翰林汇17、k＜1且k　　　 翰林汇18、－2＜k＜2或k＞5翰林汇

三、 19、 左焦点（－5，0），直线方程为y = x＋5代入得7x²－90x－369 = 0,∴x₁＋x₂=,∵＜0,∴A，B在双曲线的两支上，∴F₁A = ex_A＋a,F₁B=－(ex_B＋a)∴AB = F₁A－F₁B = ex_A＋a＋ex_B＋a = e(x_A＋x_B)＋2a=.翰林汇

20、

－∴1-cos = 1，.翰林汇

21、 切线方程为4x－y = 17,渐近线方程为4xy = 0,设双曲线方程为16x²－y² = 点A坐标代入得，∴所求双曲线方程为16x²－y² = 255 .翰林汇

22、证明：

　　　　　　　　

  又PF₁－PF₂=2a ∴

∴. ∴=1.翰林汇

23、证明： 如图：PF₁=PM＋MF₁=PM＋F₁A ① PF₂=PN＋NF₂=PN＋F₂A ②

又PF₁－PF₂=2a　F₁A＋F₂A=F₁F₂=2c，PM=PN

①－②得F₁A－F₂A=F₁F₂－F₂A－F₂A=2a

∴2F₂A=2c－2a ∴F₂A=c－a

　　　　

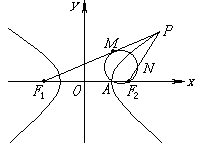
∴A(a,0)即A为双曲线一个顶点,同理可证,点P在左支上时,点A′(－a,0).

翰林汇