2006年江苏省高考数学立体几何最后押题

1．直四棱柱ABCD－A₁B₁C₁D₁中，底面ABCD为等腰梯形，AB＝2CD，AA₁＝AD＝CD＝1.

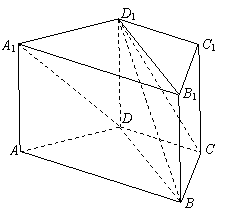求：（1）AD与BD₁所成的角；

（2）AB与面BB₁D₁D所成的角：

（3）求面A₁DD₁与面BCD₁所成锐二面角的大小.

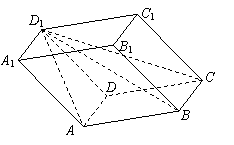
2．如图，四棱柱ABCD－A₁B₁C₁D₁中，平面B₁AC与底面ABCD垂直，B₁A、B₁B、B₁C与底面ABCD所成的角均为45°，AD//BC，且AB=BC=2AD.

（1）求证：四边形ABCD是直角梯形；

（2）求异面直线AA₁与CD所成角的大小；

（3）求AC与平面AB₁B所成角的大小。

3．如图，已知四棱柱ABCD－A₁B₁C₁D₁，BD₁⊥AD，AA₁＝AD＝2，∠ADD₁＝60°，底面ABCD为菱形，二面角D₁－AD－B的大小为120°.

(Ⅰ)求BD₁与底面ABCD所成角的大小;

(Ⅱ求二面角A－BD₁－C的大小.

2006年江苏省高考数学立体几何最后押题参考答案

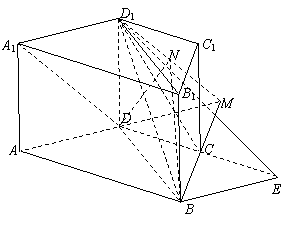1．解：(1)过B作BE//AD，且BE=AD，连CE、D₁E，则∠D₁BE为AD与D₁B所成角或其补角，在Rt△D₁DE中，求得D₁E＝，在△ABD中由余弦定理得BD＝，

在Rt△D₁BD 中D₁B=2，在△D₁BE中，

D₁B²＋BE²＝D₁E²，∴∠D₁BE＝90°，

所以AD与D₁B成的角为90⁰.

（也可以通过证明线面垂直来证明）

（2）由（1）AD⊥D₁B，

又AD⊥D₁D，∴AD⊥平面D₁BD，

所以∠ABD为AB平面D₁BD所成角，

在Rt△ABD中，∠ABD=30⁰

（3）延长AD、BC相交于点M，

连接D₁M，则D₁M为平面D₁AD与平面D₁BC的交线，

易证BD⊥平面D₁AD，过D作DN⊥D₁M，连BN，

则由三垂线定理，得BN⊥D₁M，

∴∠BND为平面D₁AD与平面D₁BC所成的角，在△ABM中，AB＝2CD，

∴D为AM的中点，DM＝AM＝1，在Rt△D₁DM中，D₁D＝DM＝1，

D₁M＝，∴DN⊥D₁M，∴DN＝ D₁M＝

在Rt△BDN 中，BD＝，DN＝，

∴tan∠BND＝＝.

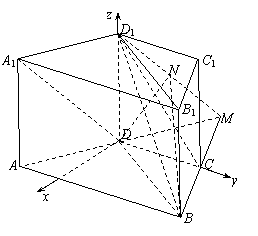
方法二：（1）（向量法）建立如图所示的空间直角

坐标系D－xyz，则D(0，0，0)，A(，－，0）

B(，，0)，D₁ (0，0，1)，C(0，1，0)，

＝(－，，0），＝(，，－1)，

∴·＝－＋＋0＝0，∴AD⊥D₁B，故AD与D₁B所成的角为90°.

（2）同法一

（3）由（1）知AD⊥D₁B，又D₁D⊥平面ABCD，∴AD⊥BD，平面D₁AD⊥平面ABCD，∴BD⊥平面D₁AD，故平面D₁AD的法向量为n₁＝＝(－，－，0)，

设平面D₁BC的法向量为n₂＝(x，y，1)，由n₂⊥BC，n₂⊥D₁B，

＝(－，－，0），＝(，，－1)，得

Þ∴ n₂＝(－，1，1)，

cos< n₁，n₂>＝＝＝－,

所以平面D₁AD与平面D₁BC所成锐二面角的大小为arccos.

2．解：方法一（1）证明：作B₁O⊥AC交AC于点O，连接OB.

∵面B₁AC⊥ABCD，所以B₁O⊥ABCD，

∵侧棱B₁A、B₁B、B₁C与底面ABCD所成的角均为45°，

∴∠B₁AO=∠B₁BO=∠B₁CO=45°，

∴△ B₁AO≌△B₁BO≌△B₁CO，所以B₁A= B₁B= B₁C，OA=OB=OC，

∴AC是△ABC外接圆的直径，所以AB⊥BC，又AD//BC，AD≠BC，

∴四边形ABCD是直角梯形.

（2）分别取BC中点M，B₁C中点N，连结AM，AN，MN，则MN//B₁B∥A₁A，又AD//BC，AD=BC=MC，所以，ADCM为平行四边形，所以AM//DC，

所以∠AMN是异面直线AA₁与CD所成角.

由（1），△B₁AO，△B₁BO，△B₁CO是全等的等腰直角三角形，

AB=BC，所以，△B₁AC，△BAC是全等的等腰直角三角形.

设B₁O=a，则MN=B₁B=，AM=

因为AM=AN，所以在等腰三角形AMN中，

所以，异面直线AA₁与CD所成角为

（3）取B₁B中点E，连结AE、CE、OE，由（2）知AE⊥B₁B，CE⊥B₁B，

∴B₁B⊥平面AEC，∴平面B₁AB⊥平面AEC，且交线就是AE，

∴AC在平面B₁AB上的射影是AE，∴∠CAE是AC与平面B₁AB所成的角

在等腰直角三角形B₁OB中，E是B₁B的中点，

∴

∴直线AC与平面B₁AB所成角的大小是

方法二（1）证明：作B₁O⊥AC交AC于点O，连OB，∵面B₁AC⊥面ABCD，

∴B₁O⊥面ABCD,∵侧棱B₁A、B₁B、B₁C与底面ABCD所成的角均为45°，

∴∠B₁AO=∠B₁BO=∠B₁CO=45°，∴△B₁AO≌△B₁BO≌△B₁CO，

∴B₁A= B₁B= B₁C，OA=OB=OC=OB₁，又AB=BC，所以OB⊥AC，

∴OA、OB、OB₁所在射线分别作为非负x轴、非负y轴、非负z轴

建立空间直角坐标系，设OB₁=a，则A（a，0，0），B（0，a，0），C（－a，0，0），

B₁（0，0，a），∴

∴∴四边形ABCD是直角梯形

（2）由（1），△B₁AO，△B₁BO，△B₁CO是全等的等腰直角三角形，

∴△B₁AC，△BAC是全等的等腰直角三角形.

则

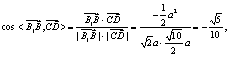
∴异面直线B₁B，CD所成角的大小是

（3）设是平面B₁AB的法向量.

则由，取

则

设AC与平面AB₁B所成角的大小为，则

所以AC与平面AB₁B所成角的大小是.

3．(Ⅰ)解：如图,作D₁O⊥平面ABCD,垂足为点O.连结OB、OA、OD，

OB与AD交于点E,连结PE.则∠D₁BO为BD₁与底面ABCD所成的角。

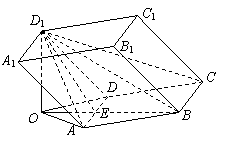∵AD⊥D₁B,∴AD⊥OB,

∵D₁A=D₁D,∴OA=OD,

于是OB平分AD,点E为AD的中点,

所以D₁E⊥AD.

由此知∠D₁EB为二面角D₁－AD－B的平面角,

∴∠D₁EB=120°,∠D₁EO=60°

由已知可求得D₁E=，，BE＝，

∴D₁O=D₁E·sin60°＝×＝，OE＝D₁E＝，

OB＝OE＋EB＝，tan∠D₁BO＝=，∠D₁BO＝30°，

即BD₁与底面ABCD所成角的大小为30°.

(Ⅱ)解法1：如图建立直角坐标系,其中O为坐标原点,x轴平行于DA.

D₁(0,0,)，B(0,,0)，D₁B中点G的坐标为(0,,0)，连结AG.

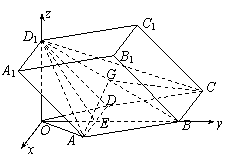又知A(1,,0),C(－2,,0)，由此得到：

＝(1，－，－)，=(0，，－)

于是有·＝0，·＝0

所以⊥，⊥，

与的夹角θ等于所求二面角的平面角,

于是cosθ=＝－，所以所求二面角的大小为p－arccos.

注：也可先求两个平面的法向量，转化为两法向量的夹角。

解法2：如图,取D₁B的中点G,PC的中点F,连结EG、AG、GF,则AG⊥D₁B,FG//BC,FG=BC.∵AD⊥D₁B,∴BC⊥D₁B,FG⊥D₁B,∴∠AGF是所求二面角的平面角.

∵AD⊥面D₁OB,∴AD⊥EG.又∵D₁E=BE,∴EG⊥BD₁,且∠D₁EG=60°.

在Rt△D₁EG中,EG= D₁E·cos60°=.在Rt△D₁EG中,EG=AD=1.

于是tan∠GAE=,又∠AGF=p－∠GAE.

所以所求二面角的大小为p－arctan.