广州育才中学2005届高三11月月考数学试题
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有 一项是符合题目要求的．
1、
已知复平面XOY内的平面向量
表示的复数分别为-2+ i,3+2i, 1+5i,则向量
表示的复数为（ ）
A、4-5i B、4-4i C、 2+8i D、3-2i
2、设集合A={ x│
＜0，x
R 
,N={x││x︱＜2,xR ，则（ ）
A、 NM B、M∩N=M C、M∪N=M D、M∪N=R
3、若
＜
＜ 0 ，则下列结论不正确的是（ ）
A、
＜b2 B、 ab＜b2 C、 
＞2 D、︳a∣
+ ︳b∣＞︳a+b∣
4、直线
互相平行的一个充分条件是（ ）
A、
都平行于同一个平面
B、与同一个平面所成的叫相等
C、
平行于
所在的平面
D、都垂直于同一个平面
5、若二项式
的展开式的第5项是常数项，则自然数n的值为（ ）
A、6 B、10 C、 12 D、15
6、已知
（ ）
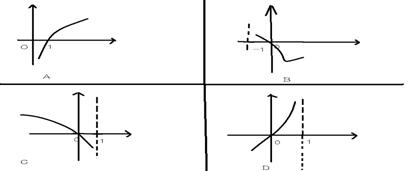
7、函数y=log2(1-x)的图象是（ ）
 |
8、
则实数x的取值范围是（ ）
A、[-1，5] B、（-1，5） C、[-1，5] D、（-5，5）
9、设函数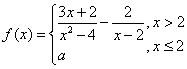
在
处连续，则
(A)
(B)
(C)
(D)
10、已知函数y=f(x)是R上的偶函数，且在（-∞，0
上是减函数，若f（a）≥
f（2），则实数a的取值范围是（ ）
A、a≤2 B、 a≤-2或a≥2 C、a≥-2 D、 -2≤a≤2
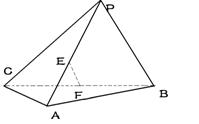11、如图，E、F 分别是三棱锥P-ABC的棱AP、BC的中点，
PC=10,AB=6,EF=6则异面直线XB与PC所成角
A、 60° B、45° C、30° D、120°
12、圆心在抛物线y2=2x(y＞0)上，并且与抛物线的准线及x轴都相切的方程是（）
二、填空题：本大题共4小题，每小题4分，共16分．
13、若
是数列
的前n项和，=
，则
=
14若x,y 满足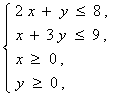
则z=x+2y的最大值为
15、从1，2，……，9这九个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是_________.
16、若对n个向量
…
存在n个不全为零的实数
…
，使得
…
=0成立，则称向量…为“线性相关”，依此规定，能说明
“线性相关”的实数、
依次可以取_____________________（写出一组数就可）。
三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．
17、（10分）设集合
若A∩B =ф，求实数a的取值范围。
18、（12分）如图，在棱长为
的正方体
中，E、F分别是棱AB和BC的中点。
（1）求二面角
的大小,
（2）求点D到平面
的距离。
19、设函数f(x)=a·b，其中向量a=(2cosx，1)，b=(cosx， 
sin2x)，x∈R.
（Ⅰ）若f(x)=1－且x∈[－
，]，求x； （Ⅱ）若函数y=2sin2x的图象按向量c=(m，n)(m<
)平移后得到函数y=f(x)的图象，求实数m、n的值。
20、某工厂生产某种产品，已知该产品的月生产量
（吨）与每吨产品的价格
（元/吨）之间的关系式为：
,且生产x吨的成本为
（元）.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）
21.(14分) 已知a为实数，
（Ⅰ）求导数
；（Ⅱ）若
，求
在[--2，2] 上的最大值和最小值；
（Ⅲ）若在（—∞，—2]和[2，+∞）上都是递增的，求a的取值范围.
22(14分). 已知函数f(x)=a1x+a2x2+…+anxn(n∈N*)，且a1，a2，a3，…，an构成数列{an}，又f(1)=n2．
（1）求数列{an}的通项公式；
（2）求证：
广州育才中学2005届高三第三次月考试题（2004.11）
数学简要参考答案
一、选择题（每题5分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | D | D | C | A | C | B | C | B | A | D |
二、填空题（每题4分）
13、33 14、7
15、11/21
16、只要
成立即可
17、解：A={X-3＜X＜-
，B=
∵A∩B = ф∴a+2≤-3或a-2≥
∴a≤-5或
18、（1）作BG⊥
，根据三垂线定理得EG⊥
∴
是二面角的平面角∴
∴
（2）等积转换
，∴d=a
另外可以用平面法向量解
19、解：（Ⅰ）依题设，f(x)=2cos2x+sin2x=1+2sin(2x+
).
由1+2sin(2x+)=1－，得sin(2 x +)=－
.
∵-≤x≤，∴-≤2x+≤
，∴2x+=-，
即x=-
.
（Ⅱ）函数y=2sin2x的图象按向量c=(m，n)平移后得到函数y=2sin2(x－m)+n的图象，即函数y=f(x)的图象.
由（Ⅰ）得
f(x)=2sin2(x+
)+1.
∵m<，∴m=-，n=1.
20. 解：每月生产x吨时的利润为
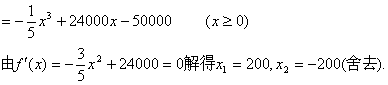
，故它就是最大值点，且最大值为：
答：每月生产200吨产品时利润达到最大，最大利润为315万元.
21. 解: (Ⅰ)由原式得
∴
(Ⅱ)由 得
,此时有
.
由得
或x=-1 , 又
所以f(x)在[--2,2]上的最大值为
最小值为
(Ⅲ)解法一: 
的图象为开口向上且过点(0,--4)的抛物线,由条件得
即
∴--2≤a≤2.
所以a的取值范围为[--2,2].
解法二:令
即
由求根公式得: 
所以在
和
上非负.
由题意可知,当x≤-2或x≥2时, ≥0,
从而x1≥-2, x2≤2,
即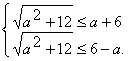
解不等式组得: --2≤a≤2.
∴a的取值范围是[--2,2].
22．（1）由题意：f(1)=a1+a2+…+an=n2，(n∈N*)
n=1时，a1=1
n≥2时，an=(a1+a2+…+an)-(a1+a2+…+an-1)=n2-(n-1)2=2n-1
∴对n∈N*总有an=2n-1,即数列{an}的通项公式为an=2n-1.
(2)
