文科高三复习作业（8）

班级　　 姓名　　 座号　　

1、若O为△ABC的内心，且满足，则△ABC的形状为 （　 ）

　　　  A．等腰三角形　 　 B．正三角形　　　　 　C．直角三角形　　 D．以上都不对

_2、已知，则a+b的取值范围是　　　　　　　　　　　　　　　　　　 　　 （ 　）

A．（0，+∞）　　　　　　　　 　 B．（0，2）∪（2，+∞）

C．（－，2）∪（2，+∞）　　　 D．（－，+∞）

3、在100，101，102，…，999这些数中各位数字按严格递增（如“145”）或严格递减（如

　“321”）顺序排列的数的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　 ）

　　　 A．120　　　　　　　　　　 B．168　　　　　　　　　　 C．204　　　　　　　　　　 D．216

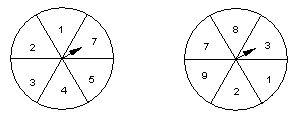
4、如图所示，在两个圆盘中，指针在本圆盘每个数所在区域的机会均等，那么两个指针同时落在奇数所在区域的概率是　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　（.　 ）

A．　　　　　　　　　　　　　B．　　　　　　　　　　　　　C．　　　　　　　　　　　　　D．

5、的三个顶点的坐标为，，，点在内部及边界上运动，则的最大值为　　　　，最小值为　　　　。

6、、为两等差数列，=，则=____　  _.

7、把曲线按向量a=（1，2）平移后得到曲线C₂，曲线C₂有一条准线方程为x=5，则k的值为　　　　 ；离心率e为　　　　　 .

8、已知函数的图象与函数g（x）的图象关于直线y=x对称，令，则关于函数h（x）有下列命题：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 ①函数h（x）的图象关于原点对称；　　　　②函数h（x）为偶函数；

　　　 ③函数h（x）的最小值为0；　　　　　　　　　 ④函数h（x）在（0，1）上为减函数.

　　　 其中，正确命题的序号是　　　　　　　 （注：将所有的正确命题的序号都填上）

9、已知处有极值，其图象在x=1处的切线与直线6x+2y+5=0平行　（1）求函数的单调区间；　　　 （2）求函数的极大值与极小值的差；

　　　　　 （3）若x求实数c的取值范围.

10、设G、M分别为不等边△ABC的重心与外心，A（－1，0），B（1，0），且.

　 （1）求点C的轨迹E的方程；

　 （2）是否存在直线l，使l过点（0，1），并与曲线E交于P、Q两点，且满足？

若存在，求出直线l的方程；若不存在，说明理由.

作业（8）答案：1、A　2、B　3、B　4、A　5、4, -2　6、　7、－3，　 8、②③

9、解：1．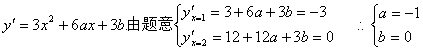

2．由（1）知x=0时取极大值C . x=2时取极小值c－4

∴极大值与极小差之差为4.

3．函数在区间[1，3]上有最小值f (2)=c－4，要使

10、解（1）设其中，设外心M（0，m），由于，

故，得

整理得轨迹E的方程是 （4分）

（2）假设存在直线l满足题设条件，由题设知l的方程为，

化简得

设，则

　 ①　　　　　　 　　 ②

由即（8分）

结合①②得

故存在直线　 （12分）