高考数学不等式专题测试试卷
班级 .姓名 .得分 .
一、填空题:(每小题5分,共70分)
1.不等式![]() 的解集是
.
的解集是
.
2.设A={xx2-2x-3>0},B={xx2+5x≤0},则![]() 等于
.
等于
.
3. 若0<x<![]() , 函数y=x(1–2x)的最大值是
.
, 函数y=x(1–2x)的最大值是
.
4.设![]() ,函数
,函数![]() 有最小值,则不等式
有最小值,则不等式![]() 的解集为 。
的解集为 。
5.若关于x的不等式ax2-ax+1>0对于x∈R恒成立,则实数a的取值范围是 .
6.若实数a、b满足a+b=2,则3a+3b的最小值是 .
7.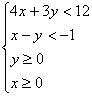 表示的平面区域内的整点的个数是
.
表示的平面区域内的整点的个数是
.
8.建造一个容积为18 m3,深为2 m的长方体无盖水池,如果池底和池壁每平方米的造价分别为200元和150元,那么池的最低造价为 (元)
9.设![]() ,则
,则![]() 的大小关系是
的大小关系是
10.不等式(x-2)(x+1)<0解集为
11.设![]() 满足约束条件:
满足约束条件: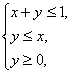 则
则![]() 的最大值是
的最大值是
12.已知方程![]() 有两个正实数根,则实数
有两个正实数根,则实数![]() 的取值范围是_____________
的取值范围是_____________
13.若![]() 的最大值是
.
的最大值是
.
14.已知集合![]() ,
,![]() 则
则![]() .
.
二、解答题:(6小题,共90分)
15.(14分)解关于![]() 的一元二次不等式
的一元二次不等式![]()
16.(14分)二次函数![]() 的图象开口向下,且满足
的图象开口向下,且满足![]() 是等差数列,
是等差数列,![]() 是等比数列,试求不等式
是等比数列,试求不等式![]() 的解集。
的解集。
17.(15分)已知数列![]() 满足
满足![]() ,
,![]() 是其前
是其前![]() 项和,且
项和,且![]() ,二次函数
,二次函数![]() 的图象与
的图象与![]() 轴有两个交点
轴有两个交点![]() ,且
,且![]() ,试求
,试求![]() 的值。
的值。
18.(15分)某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨,二级子棉1吨;生产乙种棉纱1吨需耗一级子棉1吨,二级子棉2吨;每一吨甲种棉纱的利润是600元,每一吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨。甲、乙两种棉纱应各生产多少吨,才能能使利润总额最大?
19.(16分)如图,动物园要围成相同面积的长方形虎笼四间。
一面可利用原有的墙,其他各面用钢筋网围成。
⑴现有可围成36![]() 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
 ⑵若使每间虎笼的面积为24
⑵若使每间虎笼的面积为24![]() ,则每间虎笼的长、宽各设计为多少时,可使围成的四间虎笼的钢筋网总长最小?
,则每间虎笼的长、宽各设计为多少时,可使围成的四间虎笼的钢筋网总长最小?
20.设函数f(x)=logb![]() (b>0且b≠1),
(b>0且b≠1),
(1)求f(x)的定义域;
(2)当b>1时,求使f(x)>0的所有x的值。
答案
1.(-2,1) 2.![]() 3.
3.![]() , 4.
, 4.![]() 5..
5..![]()
6.6 7.2个 8.5400 9.![]() 10
10
![]() 11.2
11.2
12.![]() 13.
13.![]() 14.
14.![]()
15. 解:(14分)∵![]() ,∴
,∴![]()
⑴当![]() ,不等式解集为
,不等式解集为![]() ;
;
⑵当![]() 时,不等式为
时,不等式为![]() ,解集为
,解集为![]() ;
;
⑶当![]() ,不等式解集为
,不等式解集为![]() ;
;
16.解:(14分)由已知条件得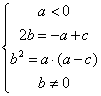
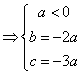 ∴不等式
∴不等式![]() 即为
即为![]() ,又∵
,又∵![]() ,∴
,∴![]() ,
,![]() 。故不等式
。故不等式![]() 的解集为
的解集为![]() 。
。
17.解:(15分)∵数列![]() 满足
满足![]() ,∴数列
,∴数列![]() 是等差数列,且公差
是等差数列,且公差![]() ,又∵
,又∵![]() ,∴
,∴![]() 又
又![]() ,∴
,∴![]() ,从而
,从而![]() ,
,![]() 。
。
∴![]() ,由于
,由于![]() ,又
,又![]() ,∴
,∴![]() 的图象的开口向上,与
的图象的开口向上,与![]() 轴有两个交点
轴有两个交点![]() ,依题意有
,依题意有
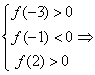
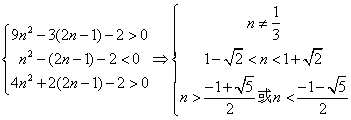 ,
,
由于![]() ,故
,故![]() 。
。
18.解:(15分)先列出下面表格
| 一级子棉(t) | 二级子棉(t) | 利润(元) | |
| 甲种棉纱(t) | 2 | 1 | 600 |
| 乙种棉纱(t) | 1 | 2 | 900 |
| 限制条件 | 不超过300t | 不超过250t |

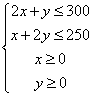
设生产甲种棉纱![]() 吨,乙种棉纱
吨,乙种棉纱![]() 吨,
吨,
总利润为![]() 元,依题意得
元,依题意得
目标函数为:![]()
作出可行域如图阴影所示。
目标函数可变形为
![]() ,从图上可知,当
,从图上可知,当
直线![]() 经过可行域的
经过可行域的![]() 点时,直线的截距
点时,直线的截距![]() 最大,从而
最大,从而![]() 最大。
最大。

![]()
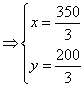 ,即
,即![]() 。故生产甲种棉纱
。故生产甲种棉纱![]() 吨,乙种棉纱
吨,乙种棉纱![]() 吨时,总利润最大。最大总利润是
吨时,总利润最大。最大总利润是![]() (元)
(元)
19.解:(16分)⑴设每间虎笼长为![]() ,宽为
,宽为![]() ,
,
则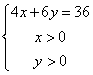 ,面积
,面积![]() 。由于
。由于
![]() ,所以
,所以![]() ,即
,即![]() ,当
,当
且仅当![]() 时取等号。
时取等号。![]() ,所以,每间虎笼长、宽
,所以,每间虎笼长、宽
分别为![]() 时,可使面积最大。
时,可使面积最大。
⑵设围成四间虎笼的钢筋网总长为![]() ,则
,则![]() ,所以
,所以
![]() ,当
,当
且仅当![]() 时取等号。
时取等号。![]() 。故每间虎笼长、宽分别为
。故每间虎笼长、宽分别为![]() 、
、![]() 时,可使钢筋的总长最小,为
时,可使钢筋的总长最小,为![]() 。
。
20解 (1)∵x2-2x+2恒正,
∴f(x)的定义域是1+2ax>0,
即当a=0时,f(x)定义域是全体实数。
当a>0时,f(x)的定义域是(-![]() ,+∞)
,+∞)
当a<0时,f(x)的定义域是(-∞,-![]() )
)
(2)当b>1时,在f(x)的定义域内,f(x)>0![]()
![]() >1
>1![]() x2-2x+2>1+2ax
x2-2x+2>1+2ax
![]() x2-2(1+a)x+1>0
x2-2(1+a)x+1>0
其判别式Δ=4(1+a)2-4=4a(a+2)
(i)当Δ<0时,即-2<a<0时
∵x2-2(1+a)x+1>0
∴f(x)>0![]() x<-
x<-![]()
(ii)当Δ=0时,即a=-2或0时
若a=0,f(x)>0![]() (x-1)2>0
(x-1)2>0
![]() x∈R且x≠1
x∈R且x≠1
若a=-2,f(x)>0![]() (x+1)2>0
(x+1)2>0
![]() x<
x<![]() 且x≠-1
且x≠-1
(iii)当△>0时,即a>0或a<-2时
方程x2-2(1+a)x+1=0的两根为
x1=1+a-![]() ,x2=1+a+
,x2=1+a+![]()
若a>0,则x2>x1>0>-![]()
∴![]() 或
或![]()
若a<-2,则![]()
∴f(x)>0![]() x<1+a-
x<1+a-![]() 或1+a+
或1+a+![]() <x<-
<x<-![]()
综上所述:当-2<a<0时,x的取值集合为![]() xx<-
xx<-![]()
![]()
当a=0时,x∈R且x≠1,x∈R,当a=-2时:![]() xx<-1或-1<x<
xx<-1或-1<x<![]()
![]()
当a>0时,x∈![]() xx>1+a+
xx>1+a+![]() 或-
或-![]() <x<1+a-
<x<1+a-![]()
![]()
当a<-2时,x∈![]() xx<1+a-
xx<1+a-![]() 或1+a+
或1+a+![]() <x<-
<x<-![]()
![]()