_{洪泽县中学2005---2006学年高三教学质量检测}

_{数　 学　 试　　卷　　　2002-2-20}

_{命题人：刘永贵}

_{第Ⅰ卷(选择题，共60分)}

_{一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.)}

_{1．设是集合M到集合N的映射，下列说法正确的是　　　  （　A 　）}

_{A．M中每一个元素在N中必有象　　　　B.N中每一个元素在M中必有原象}

_{C．N中每一个元素在N中的原象是唯一的D.N是M中所有元素的象的集合} 

_{2. 若的夹角为，且，则m的值是　　　　　　　　　　　　　　　　　　　　　　　　　　　  （ C 　）}

_{A.　0　　　 B.　1或-6　　 C.　-1或6　　　　D.　 6或-6}

_{3．已知两点P(4,-9),Q(-2,3),则y轴与直线PQ的交点分有向线段所成的比为( C　)}

_{A.　　　　B.　 　　　 C.　　2　　　　   D.　　3}

_{4．若实数a、b满足ab<0，则有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （ D　 ）}

_{A．a－b<a－b　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．a－b<a+b}

_{C．a+b>a－b　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D．a+b<a－b}

_{5．已知p是r的充分条件，s是r的必要不充分条件，q是s的必要条件，则p是q（　）}

_{A. 充分不必要条件　　　　　　　　　　 B. 必要不充分条件}

_{C. 充要条件　　　　　　　　　　　　　 D. 既非充分也非必要条件}

_{6．已知数列满足：，，则等于　　　　 (A　 )}

_{A.　 2　　　　 B.  　　　C.  　 　 D.  1}

_{7．不等式组有解，则实数a的取值范围是　　　　　 （　）}

_{A． （-1，3）　　　　　　　　　 B．（-3，1）}

_{C． （-∞，1）（3，＋∞）　　 D．（-∞，-3）（1，＋∞）}

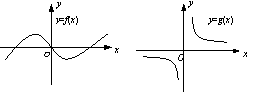_{8．已知y=f(x)与y=g(x)的图象如图所示，}

_{则函数F(x)=f(x)·g(x)的图象可以是}

_{（　A  ）}

_{9.不等式对任意都成立，则的取值范围为（　B  ）}

_{A.　 　　　B.　 　　C.　　　D.}

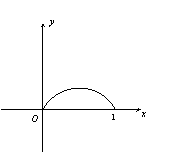_{10．已知函数f (x)（0 ≤ x ≤1）的图象的一段圆弧（如图所示）若，则（ C ）}



 _{A．　　　　　　 B．}

_{C．　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．前三个判断都不正确}

_{11．已知函数y = 2sin(ωx)在［，］上单调递增，则实数ω的取值范围是（ A ）}

_{A．（0，　　　　　　　　　　　　　B．（0，2　　　　　　　　　　　　　　　　　 C．（0，1　　　　　　　　　　　　　　　　　 D．} 

_{12．.等比数列中，，公比，用表示它前n项的积：，则中最大的是　　　　　　　　　　　　　　　　　　　　  （ C ）}

_{A.　 　 B.　 　 C.　 　　D.}

_{二、填空题：本大题共4小题，每答案填在题中横线上,每小题4分,共16分.}

_{13. cos2α+cos2(α+120°)+cos2(α+240°)的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。}

_{【解】　本题的隐含条件是式子的值为定值，即与α无关，故可令α=0°，计算得上式值为。}

_{14.若指数函数的部分对应值如下表：} 

	-2	0	2
	0.69	1	1.44

_{则不等式的解集为　　　　　　   。}

_{15. 若关于x的方程=k(x-2)有两个不等实根，则实数k的取值范围是　　　　　　　　　。}

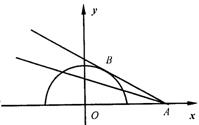_{【解】　令y1=,y2=k(x-2),由图可知kAB<k≤0，其中AB为半圆的切线，计算kAB= -,∴-<k≤0。}

 

_{16.若在所给条件下，数列的每一项的值都能唯一确定，则称该数列是“确定的”，在下列各组条件下，有哪些数列是“确定的”？请把对应的序号填在横线上　　　　。①②③}

_{①是等差数列，（这里是的前项和，为实常数，下同）}

_{②是等差数列，}

_{③是等比数列，}

_{④是等比数列，}

_{三、解答题:本大题共6小题，共84分．解答应写出文字说明，证明过程或或演算步骤．}

_{18.(本题12分).△ABC的三边为a，b，c，已知，且，求}

_{三角形面积的最大值．}

_{解：，又由余弦定理得}

_{．，，得，．又，．}

_{当且仅当时，等号成立．．}

_{19.(本题12分).已知函数f（x）的图像与函数的图像关于点A（0，1）对称．}

_{（1）求f（x）的解析式；}

_{（2）若，且在区间（0，2]上为减函数，求实数a的取值范围；}

_{解:（1）设f（x）图像上任一点坐标为（x，y），点（x，y）关于点A（0，1）的对称点（-x，2-y）在h（x）图像上}

_{∴　，　∴　，即}

_{（2），即在（0，上递减，　∴　a≤-4}

_{20.(本题12分)设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a).}

_{求： (1).写出f(a)的表达式；}

_{（2）.试确定能使f(a)=的a的值,并求此时函数y的最大值.}

_{解析: (1).y=2(cosx--.} 

 

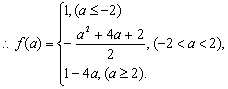
_{(2).当a≤-2时,f(a)=1,从而f(a)=无解;当-2<a<2时,由得a2+4a-3=0,解之得a=-1或a=-3(舍去);当a≥2时,由1-4a=得a=(舍去).综上所述a=-1,此时有y=2(cosx+,当cosx=1时,即x=2k(k时,y有最大值为5.}

_21．

_{20．（本小题满分12分）}

_{设数列{an}和{bn}满足a1=b1=6, a2=b2=4, a3=b3=3, 且数列{an+1－an }（n∈N*）是等差数列，数列{bn－2}(n∈N*)是等比数列.}

_{（Ⅰ）求数列{an}和{bn}的通项公式；}

_{（Ⅱ）是否存在k∈N*，使ak－bk∈（0，）？若存在，求出k；若不存在，说明理由.}

_{20．解：（I）由已知a2－a1=－2, a3－a2=－1, －1－(－2)=1}

_{∴an+1－an=(a2－a1)+(n－1)·1=n－3}

_{n≥2时，an=( an－an－1)+( an－1－an－2)+…+( a3－a2)+( a2－a1)+ a1}

_{=(n－4)+(n－5) +…+(－1)+(－2)+6}

₌

_{n=1也合适.　∴an=　(n∈N*) ……………………3分}

_{又b1－2=4、b2－2=2 .而　∴bn－2=（b1－2）·()n－1即bn=2+8·()n…6分}

_{∴数列{an}、{bn}的通项公式为：an= ，bn=2+()n－3}

_（II）设

_{当k≥4时为k的增函数，－8·()k也为k的增函数，而f(4)=}

_{∴当k≥4时ak－bk≥………………10分}

_{又f(1)=f(2)=f(3)=0　 ∴不存在k，　　　　 使f(k)∈（0，）…………12分}

_{22 (本题12分).已知在R上单调递增，记的三内角的对应边分别为，若成等差数列时，不等式恒成立．}

_{（1）求实数的取值范围；（2）求角B的取值范围；（3）求实数的取值范围．}

_{(1)由知，在R上单调递增，恒成立，且，即且，； 当，即时，，时，时，，即当时，能使在R上单调递增，∴．}

_{(2)成等差数列，∴，由余弦定理：cosB==}

_=，∴，

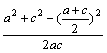
_{(3) 在R上单调递增，且，}

_所以，即

_而，

_{故，即，，即，即．}