苏州中学高三数学练习(8)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是
A.81.2,4.4 B.78.8,4.4 C.81.2,84.4 D.78.8,75.6
2. 下表是某市7个县级行政管理区人口数与土地面积:
| 行政区代号 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 人口(万) | 63.46 | 59.44 | 103.23 | 38.11 | 21.67 | 6.46 | 6.61 |
| 面积(万 km2) | 0.33 | 0.20 | 0.45 | 0.15 | 0.07 | 0.02 | 0.02 |
经统计比较可知,其中人口密度(人口/面积)最大的行政区是
A.x2 B.x3 C.x5 D.x7
3. .已知p=2![]() ,q=3,p、q的夹角为
,q=3,p、q的夹角为![]() ,如下图所示,若
,如下图所示,若![]() =5p+2q,
=5p+2q,![]() =p-3q,且D为BC的中点,则
=p-3q,且D为BC的中点,则![]() 的长度为
的长度为
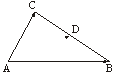
A.![]() B.
B.![]() C.7 D.8
C.7 D.8
4.函数f(x)=b(1-![]() )+ a sinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在
)+ a sinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在
(-∞,0)上有
A.最大值10 B.最小值-5 C.最小值-4 D.最大值13
5.如果![]() ≠kx对一切x≥15均成立,则有
≠kx对一切x≥15均成立,则有
A.k≤0 B.k≤0或k>![]() C.k≤0或k>
C.k≤0或k>![]() D.0≤k<
D.0≤k<![]()
6. 已知函数f(x)=sinπx的图象的一部分如图(a),有以下四个函数解析式:
①y=f(2-x);②y=f(x+1);③y=f(x-![]() );④y=f(-x+1).
);④y=f(-x+1).
其中与图(b)所对应的函数解析式为
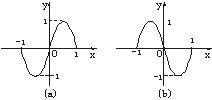
A.①② B.②③ C.③④ D.①④
7.2003年9月1日,某中学按年利率5%(利息按年以复利计算)从银行贷款500万元,用于建造一所可容纳1000人住宿的学生公寓,2004年9月1日投入使用,同时向每位学生收取一年住宿费a元用于还贷,照此方式,预计15年还清贷款,则a的值约为(提供:1.0515≈2.08)
A.412 B.482 C.500 D.512
8. 已知F1、F2分别是双曲线![]() -
-![]() =1的左、右焦点,P为双曲线左支上任一点,若
=1的左、右焦点,P为双曲线左支上任一点,若![]() 的最小值为8a,则双曲线的离心率范围为
的最小值为8a,则双曲线的离心率范围为
A.(1,3] B.(0,3] C.(1,2] D.(1,+∞)
9.设函数f(x)=(x-1)(x-2)(x-3)(x-4),则f′(x)=0有
A.分别位于区间(1,2),(2,3),(3,4)内三个根
B.四个实根分别为xi=i(i=1,2,3,4)
C.分别位于区间(0,1),(1,2),(2,3),(3,4)内四个根
D.分别位于区间(0,1),(1,2),(2,3)内三个根
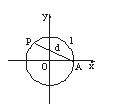
10.如下图,设点A是单位圆上的一定点,动点P从A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧![]() 的长为l,弦AP的长为d,则函数d=f(l)的图象大致为
的长为l,弦AP的长为d,则函数d=f(l)的图象大致为

二、填空题(本大题共6小题,每小题5分,共30分.把答案填在题中横线上)
11. 氨基酸的排列顺序是决定蛋白质多样性的原因之一.某肽链由7种不同的氨基酸构成,若只改变其中3种氨基酸的位置,其他4种不变,则不同的改变方法共有___________种.
12.设不等式组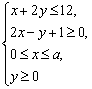 所围成的平面区域的面积为S,当6≤S≤22时,a的取值范围是___________.
所围成的平面区域的面积为S,当6≤S≤22时,a的取值范围是___________.
13.△A′B′C′是用“斜二测画法”画出的等腰直角三角形ABC的直观图,设
△A′B′C′的面积为S′,△ABC的面积为S,则![]() =_______.
=_______.
14.设x1、x2∈R,定义运算![]() :x1
:x1![]() x2=(x1+x2)2-(x1-x2)2,若x≥0,常数m>0,则动点P(x)=
x2=(x1+x2)2-(x1-x2)2,若x≥0,常数m>0,则动点P(x)=![]() 的轨迹方程是_______.
的轨迹方程是_______.
15. 记min{a,b}为a、b两数的最小值,当正数x、y变化时,t=min{x,![]() }也在变化,则t的最大值为___________.
}也在变化,则t的最大值为___________.
16.设x、y∈R,且满足 则x+y=___________.
则x+y=___________.
三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
二人掷一颗骰子,两人各掷一次,点数大者为胜,但这个骰子可能不太规则,以致k点出现的概率是Pk(k=1,2,3,4,5,6).在这种情况下,
(1)求二人平局的概率P.
(2)证明P≥![]() ;并证明如果P=
;并证明如果P=![]() ,则Pk=
,则Pk=![]() (k=1,2,3,4,5,6).
(k=1,2,3,4,5,6).
18.(本小题满分14分)
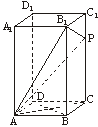
在正四棱柱ABCD—A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的一点.
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成的二面角的正切值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线?
19.(本小题满分12分)
如图,给出了一个三角形数阵,已知每一列的数成等差数列,从第3行起,每一行的数成等比数列,每一行的公比都相等.记第i行第j列的数为aij(i≥j,i、j∈N*).
![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]()
……
(1)试写出aij关于i、j的表达式,并求a83;
(2)设这个数阵共有n行,求数阵表中的所有数之和.
20.(本小题满分16分)
已知集合A={(x,y)y≥x-a},B={(x,y)y≤-ax+2a}(a≥0).
(1)证明A∩B≠![]() ;
;
(2)当0≤a≤4时,求由A∩B中点组成图形面积的最大值.
21.(本小题满分16分)已知椭圆C1:![]() +y2=1的左、右顶点分别是A、B,点P是双曲线C2:
+y2=1的左、右顶点分别是A、B,点P是双曲线C2:![]() -y2=1在第一象限部分上的一点,连结AP交椭圆C1于点C,连结PB并延长交椭圆C1于点D.
-y2=1在第一象限部分上的一点,连结AP交椭圆C1于点C,连结PB并延长交椭圆C1于点D.
(1)若直线PA与PB的斜率分别为k1、k2,求证:k1·k2是定值;
(2)若△ACD与△PCD的面积相等,求直线CD的倾斜角;
(3)直线CD的倾斜角是否会随着点P的不同而改变?并说明理由.
苏州中学高三数学试卷详细解答
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是
A.81.2,4.4 B.78.8,4.4 C.81.2,84.4 D.78.8,75.6
解析:数据变化后,平均数改变而方差不变.
答案: A
2. 下表是某市7个县级行政管理区人口数与土地面积:
| 行政区代号 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 人口(万) | 63.46 | 59.44 | 103.23 | 38.11 | 21.67 | 6.46 | 6.61 |
| 面积(万 km2) | 0.33 | 0.20 | 0.45 | 0.15 | 0.07 | 0.02 | 0.02 |
经统计比较可知,其中人口密度(人口/面积)最大的行政区是
A.x2 B.x3 C.x5 D.x7
解析: xi区的人口密度为ai(i=1,2,…,7),a1=192.30,a2=297.20,a3=229.40,a4=254.07,a5=
309.57,a6=323.00,a7=330.50.
答案: D
3. .已知p=2![]() ,q=3,p、q的夹角为
,q=3,p、q的夹角为![]() ,如下图所示,若
,如下图所示,若![]() =5p+2q,
=5p+2q,![]() =p-3q,且D为BC的中点,则
=p-3q,且D为BC的中点,则![]() 的长度为
的长度为

A.![]() B.
B.![]() C.7 D.8
C.7 D.8
解析: ![]() =
=![]() (
(![]() +
+![]() )=3p-
)=3p-![]() q,
q,
∴![]() 2=9p2+
2=9p2+![]() q2-3p·q=
q2-3p·q=![]() .
.
∴![]() =
=![]() .
.
答案: A
4.函数f(x)=b(1-![]() )+ a sinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在
)+ a sinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在
(-∞,0)上有
A.最大值10 B.最小值-5 C.最小值-4 D.最大值13
解析: 令F(x)=f(x)-3=b(1-![]() )+sinx=b
)+sinx=b![]() +sinx,
+sinx,
则F(-x)=b![]() +sin(-x)=b
+sin(-x)=b![]() -sinx=-F(x),
-sinx=-F(x),
∴F(x)为奇函数,F(x)在(0,+∞)上有最大值7.
∴F(x)在(-∞,0)上有最小值-7.
∴f(x)在(-∞,0)上有最小值-4.
答案: C
5.如果![]() ≠kx对一切x≥15均成立,则有
≠kx对一切x≥15均成立,则有
A.k≤0 B.k≤0或k>![]() C.k≤0或k>
C.k≤0或k>![]() D.0≤k<
D.0≤k<![]()
解析: 令y=![]() ,y=kx,显然k≤0时成立,
,y=kx,显然k≤0时成立,
由![]()
![]() k2x2-x+5=0(k>0),
k2x2-x+5=0(k>0),
由Δ=0,得k=![]() ;
;
由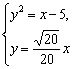 得x=10,而x≥15,
得x=10,而x≥15,
∴当x=15时,k=![]() .
.
∴k≤0或k>![]() .
.
答案: C
6. 已知函数f(x)=sinπx的图象的一部分如图(a),有以下四个函数解析式:
①y=f(2-x);②y=f(x+1);③y=f(x-![]() );④y=f(-x+1).
);④y=f(-x+1).
其中与图(b)所对应的函数解析式为
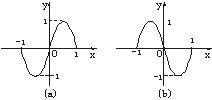
A.①② B.②③ C.③④ D.①④
解析: ∵图形(a)、(b)关于y轴对称,
∴图(b)的函数解析式为y=-f(x).
∵f(x)=sinπx,
∴①y=f(2-x)=sinπ(2-x)=sin(2π-πx)=-sinπx=-f(x)成立.
②y=f(x+1)=sinπ(x+1)=sin(π+πx)=-sinπx=-f(x).
③y=f(x-![]() )=sinπ(x-
)=sinπ(x-![]() )=sin(πx-
)=sin(πx-![]() )=-cosπx≠-f(x).
)=-cosπx≠-f(x).
④y=f(-x+1)=sinπ(-x+1)=sin(π-πx)=sinπx=f(x).
故函数解析式①②满足图(b).
答案: A
7.2003年9月1日,某中学按年利率5%(利息按年以复利计算)从银行贷款500万元,用于建造一所可容纳1000人住宿的学生公寓,2004年9月1日投入使用,同时向每位学生收取一年住宿费a元用于还贷,照此方式,预计15年还清贷款,则a的值约为(提供:1.0515≈2.08)
A.412 B.482 C.500 D.512
解析: 500(1+5%)15=0.1a(1+1.05+1.052+…+1.0514),
a=![]() ≈482(元).
≈482(元).
答案: B
8. 已知F1、F2分别是双曲线![]() -
-![]() =1的左、右焦点,P为双曲线左支上任一点,若
=1的左、右焦点,P为双曲线左支上任一点,若![]() 的最小值为8a,则双曲线的离心率范围为
的最小值为8a,则双曲线的离心率范围为
A.(1,3] B.(0,3] C.(1,2] D.(1,+∞)
解析: ∵PF2-PF1=2a,
∴![]() =
=![]() =PF1+
=PF1+![]() +4a≥2
+4a≥2![]() +4a=8a,
+4a=8a,
其中PF1=2a时等号成立.
又设P(x,y)(x≤-a),则由第二定义,得
PF1=(-x-![]() )e=-ex-a≥c-a,
)e=-ex-a≥c-a,
即2a≥c-a,∴e=![]() ≤3,又∵e>1,∴1<e≤3.
≤3,又∵e>1,∴1<e≤3.
答案: A
9.设函数f(x)=(x-1)(x-2)(x-3)(x-4),则f′(x)=0有
A.分别位于区间(1,2),(2,3),(3,4)内三个根
B.四个实根分别为xi=i(i=1,2,3,4)
C.分别位于区间(0,1),(1,2),(2,3),(3,4)内四个根
D.分别位于区间(0,1),(1,2),(2,3)内三个根
解析: f(x)=0有四根xi=i(i=1,2,3,4).故在区间(1,2),(2,3),(3,4)必存在极值点,使f′(x)=0,故选A.
答案: A
10.如下图,设点A是单位圆上的一定点,动点P从A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧![]() 的长为l,弦AP的长为d,则函数d=f(l)的图象大致为
的长为l,弦AP的长为d,则函数d=f(l)的图象大致为


解析: 连结OP,设∠AOP为θ角,
则![]() =OP·sin
=OP·sin![]() =sin
=sin![]() ,
,
即d=2sin![]() (0≤θ≤2π).
(0≤θ≤2π).
答案: C
普通高等学校招生全国统一考试仿真试卷
数 学
第Ⅱ卷 (非选择题 共100分)
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题(本大题共6小题,每小题5分,共30分.把答案填在题中横线上)
11. 氨基酸的排列顺序是决定蛋白质多样性的原因之一.某肽链由7种不同的氨基酸构成,若只改变其中3种氨基酸的位置,其他4种不变,则不同的改变方法共有___________种.
解析: 从7种不同的氨基酸中选3种,有![]() 种选法,这3种氨基酸的不同位置有2种,即
种选法,这3种氨基酸的不同位置有2种,即![]() ·2=70.
·2=70.
答案: 70
12.设不等式组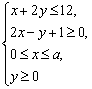 所围成的平面区域的面积为S,当6≤S≤22时,a的取值范围是___________.
所围成的平面区域的面积为S,当6≤S≤22时,a的取值范围是___________.
解析: 作出不等式组表示的可行域.
由![]()
![]() 即A(2,5).
即A(2,5).
该不等式组所表示的可行域是:直线x+2y=12的下方;直线2x-y+1=0的下方;y轴的右边,直线x=a的左边;x轴上方的区域.先从特例探求,考查梯形OBAC的面积.
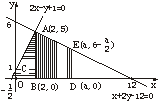
S=![]() (1+5)·2=6,满足S的下界.
(1+5)·2=6,满足S的下界.
∴a=2是最小值;
要使S取最大值22,则S梯形ABDE=16.
∴S梯形ABDE=![]() [5+(6-
[5+(6-![]() )](a-2)=16.
)](a-2)=16.
当a>2时,6-![]() >0,解得a=6,
>0,解得a=6,
∴amax=6,故a∈[2,6].
答案: [2,6]
13.△A′B′C′是用“斜二测画法”画出的等腰直角三角形ABC的直观图,设
△A′B′C′的面积为S′,△ABC的面积为S,则![]() =_______.
=_______.
解析: ![]() =
= =
=![]() .
.
答案: ![]()
14.设x1、x2∈R,定义运算![]() :x1
:x1![]() x2=(x1+x2)2-(x1-x2)2,若x≥0,常数m>0,则动点P(x)=
x2=(x1+x2)2-(x1-x2)2,若x≥0,常数m>0,则动点P(x)=![]() 的轨迹方程是_______.
的轨迹方程是_______.
解析: y=![]() =
=![]() =
=![]() ,∴y2=2mx(y≥0).
,∴y2=2mx(y≥0).
答案: y2=2mx(y≥0)
15. 记min{a,b}为a、b两数的最小值,当正数x、y变化时,t=min{x,![]() }也在变化,则t的最大值为___________.
}也在变化,则t的最大值为___________.
解析: 若x≤![]() ,
,
则t=x,t2=x2≤x·![]() ≤
≤![]() =
=![]() .
.
故t≤![]() ,当且仅当x=y=
,当且仅当x=y=![]() 时取“=”;
时取“=”;
若![]() ≤x,
≤x,
则t=![]() ,t2=(
,t2=(![]() )2≤
)2≤![]() ≤
≤![]() .
.
故t≤![]() ,当且仅当x=y=
,当且仅当x=y=![]() 时取“=”.
时取“=”.
综上可知,当x=y=![]() 时,t取最大值为
时,t取最大值为![]() .
.
答案: ![]()
16.设x、y∈R,且满足 则x+y=___________.
则x+y=___________.
解析: 由(y-1)2005+2004(y-1)=1,
变形得(1-y)2005+2004(1-y)=-1,
得知x-1=1-y![]() x+y=2.
x+y=2.
三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
二人掷一颗骰子,两人各掷一次,点数大者为胜,但这个骰子可能不太规则,以致k点出现的概率是Pk(k=1,2,3,4,5,6).在这种情况下,
(1)求二人平局的概率P.
(2)证明P≥![]() ;并证明如果P=
;并证明如果P=![]() ,则Pk=
,则Pk=![]() (k=1,2,3,4,5,6).
(k=1,2,3,4,5,6).
(1)解:P=P12+P22+…+P62. 4分
(2)证明:∵P1+P2+…+P6=1,
(P1-![]() )2+(P2-
)2+(P2-![]() )2+…+(P6-
)2+…+(P6-![]() )2
)2
=P12+P22+…+P62-![]() (P1+P2+…+P6)+
(P1+P2+…+P6)+![]()
=P-![]() ≥0,
≥0,
∴P≥![]() ,当P=
,当P=![]() 时,P1=P2=…=P6=
时,P1=P2=…=P6=![]() . 12分
. 12分
12分
18.(本小题满分14分)
在正四棱柱ABCD—A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的一点.

(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成的二面角的正切值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线?
(1)证明:∵AP在底面ABCD内的射影为AC,在正方形ABCD中AC⊥BD,∴AP⊥BD.
3分
(2)解:延长B1P与BC的延长线交于点M,连结AM,过B作BN⊥AM于点N,连结B1N,则∠B1NB即为所求二面角的平面角,设AB=a,则BM=3a,
∴BN=![]() a.
a.
∴tan∠B1NB=![]() =
=![]() . 8分
. 8分
(3)解:设AB=a,C1P=x,要使AP在平面B1AC上的射影是∠B1AC的平分线,则∠PAB1=
∠PAC,
∴cos∠PAB1=cos∠PAC,
即![]() =
=![]() ,
,
解得x=![]() a,
a,
∴P到C1的距离是底面边长的![]() . 12分
. 12分
19.(本小题满分12分)
如图,给出了一个三角形数阵,已知每一列的数成等差数列,从第3行起,每一行的数成等比数列,每一行的公比都相等.记第i行第j列的数为aij(i≥j,i、j∈N*).
![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]()
……
(1)试写出aij关于i、j的表达式,并求a83;
(2)设这个数阵共有n行,求数阵表中的所有数之和.
解:(1)由条件易知
第i行的第1个数为
ai1=![]() +
+![]() (i-1)=
(i-1)=![]() ,
,
第i行的第j个数为aij=![]() (
(![]() )j-1,
)j-1,
∴a83=![]() ×(
×(![]() )2=
)2=![]() . 6分
. 6分
(2)设数阵中第n行的所有数之和为An,
则An=![]() (1+
(1+![]() +
+![]() +…+
+…+![]() )
)
=![]() ·
·![]() =
=![]() -
-![]() ×
×![]() .
.
设所求数之和为P,则P=![]() (1+2+…+n)-
(1+2+…+n)-![]() (1·2-1+2·2-2+…+n·2-n).
(1·2-1+2·2-2+…+n·2-n).
设S=1·2-1+2·2-2+3·2-3+…+n·2-n,
则![]() =1·2-2+2·2-3+3·2-4+…+n·2-(n+1)
=1·2-2+2·2-3+3·2-4+…+n·2-(n+1)
=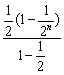 -n·2-(n+1)
-n·2-(n+1)
=1-![]() -
-![]() ,
,
则P=![]() -(1-
-(1-![]() -
-![]() ),
),
=![]() +
+![]() +
+![]() -1
-1
=![]() +
+![]() . 12分
. 12分
12分
20.(本小题满分16分)
已知集合A={(x,y)y≥x-a},B={(x,y)y≤-ax+2a}(a≥0).
(1)证明A∩B≠![]() ;
;
(2)当0≤a≤4时,求由A∩B中点组成图形面积的最大值.
(1)证明:显然(0,a)∈A.
当x=0时,y=-ax+2a=2a,
∴(0,2a)∈B.∴A∩B≠![]() . 4分
. 4分
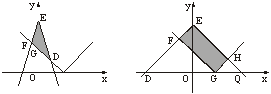
(2)解:如左上图,当2≤a≤4时,A∩B中点组成如图所示△EFD,
易得E(0,2a)、F(-![]() ,
,![]() )、D(
)、D(![]() ,
,![]() )、G(0,a).
)、G(0,a).
∴S△EFD=S△EFG+S△FGD
=![]() a·
a·![]() +
+![]() a·
a·![]()
=![]() .
.
当0<a<2时,A∩B中点组成如右上图所示四边形EFGH.
易得E(0,2a)、F(-![]() ,
,![]() )、G(a,0)、H(
)、G(a,0)、H(![]() ,
,![]() )、D(-2,0)、Q(2,0),
)、D(-2,0)、Q(2,0),
而S四边形EFGH=S△DEQ-S△DFG-S△GHQ
=![]() ×4×2a-
×4×2a-![]() (a+2)·
(a+2)·![]() -
-![]() (2-a)·
(2-a)·![]()
=![]() .
.
当a=0时,A∩B={(0,0)}.
显然适合上式,
∴S=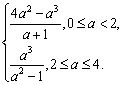 8分
8分
当0≤a<2时,S=![]() ,
,
∴S′=![]()
=![]() =
=![]()
∴S=![]() 在[0,2)上是增函数.∴0≤S<
在[0,2)上是增函数.∴0≤S<![]() .
.
当a≥2时,S=![]() ,
,
∴S′=![]() =
=![]() =
=![]() >0,
>0,
∴S=![]() 在[2,4]上是增函数.∴
在[2,4]上是增函数.∴![]() ≤S≤
≤S≤![]() .
.
综上所述,当a=4时,A∩B中点组成图形面积取得最大值![]() . 12分
. 12分
21.(本小题满分16分)
(理)已知椭圆C1:![]() +y2=1的左、右顶点分别是A、B,点P是双曲线C2:
+y2=1的左、右顶点分别是A、B,点P是双曲线C2:![]() -y2=1在第一象限部分上的一点,连结AP交椭圆C1于点C,连结PB并延长交椭圆C1于点D.
-y2=1在第一象限部分上的一点,连结AP交椭圆C1于点C,连结PB并延长交椭圆C1于点D.
(1)若直线PA与PB的斜率分别为k1、k2,求证:k1·k2是定值;
(2)若△ACD与△PCD的面积相等,求直线CD的倾斜角;
(3)直线CD的倾斜角是否会随着点P的不同而改变?并说明理由.
(1)证明:设P点的坐标为(x0,y0),则x02-4y02=4.
由A(-2,0)得k1=![]() ,
,
由B(2,0)得k2=![]() ,
,
∴k1k2=![]() =
=![]() =
=![]() 为定值. 4分
为定值. 4分
(2)解:∵△ACD与△PCD面积相等,
∴C为AP中点.
设P(x0,y0)(y0>0),则C(![]() ,
,![]() ).
).
∴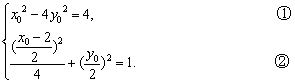
②×16+①得x02-2x0-8=0,即x0=4或x0=-2.
易知x0=-2不舍题意,∴x0=4.
∴P(4, ![]() )、C(1,
)、C(1,![]() ).
).
直线PB方程为y=![]() (x-2).
(x-2).
由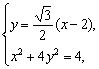 解得D(1,-
解得D(1,-![]() ).
).
∴直线CD的倾斜角为![]() . 8分
. 8分
(3)解:设直线PA、PB斜率分别为k1、k2,
直线PA、PB的方程分别为PA:y=k1(x+2)和PB:y=k2(x-2).
由![]() 得(1+4k12)x2+16k12x+(16k12-4)=0.
得(1+4k12)x2+16k12x+(16k12-4)=0.
此方程两根分别为A、C横坐标,
所以xC-2=-![]() . ①
. ①
由![]() 得
得
(1+4k22)x2-16k22x+(16k22-4)=0. 10分
此方程两根分别为B、D横坐标,
所以xD+2=![]() . ②
. ②
②-①得xD-xC=![]() +
+![]() -4
-4
=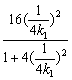 +
+![]() -4
-4
=![]() +
+![]() -4=0.
-4=0.
∴xC=xD.∴直线CD的倾斜角不会随着点P的运动而改变. 14分
