2006届浙江省乐清市柳市中学高三数学
理科模拟试卷(二)
本试卷分第Ⅰ卷(选择题)第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟。
第Ⅰ卷(选择题共50分)
一、选择题:(本大题共10小题,每小题5分 ,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若命题p::x∈A∪B则![]() p是
p是
A.![]() B.x
B.x ![]() A或x
A或x ![]() B
B
C.x ![]() A且x
A且x ![]() B D.
B D.![]()
2.已知角α的终边上一点的坐标为![]() ,则角
,则角![]() 的最小正值为
的最小正值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.一条直线穿过一个四面体,则该直线最多能与四面体的( )个面相交
A.1 B.2 C.3 D.4
4. 已知随机变量![]() ,则
,则![]() 及
及![]() 的值分别为
的值分别为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若对任意![]() 则
则![]() 是
是
A.![]() =x4 B.
=x4 B.![]() =x4-2 C.
=x4-2 C.![]() =4x3-5 D.
=4x3-5 D.![]() =x4+2
=x4+2
6.A, B, C是△ABC的三个内角,且tanA , tanB 是方程3x2-5x+1=0的两个实数根,则
△ABC是
A.钝角三角形 B.锐角三角形 C.等腰直角三角形 D.等边三角形
7.抛物线y2=2px与直线ax+y-4=0,交于两点A,B,其中点A的坐标为(1,2),设抛物
线的焦点为F,则FA+FB等于
A.7 B.![]() C.6 D.5
C.6 D.5
8.若![]() ,且
,且![]() ,则
,则![]() 和
和![]() 的夹角是
的夹角是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.若(m+i)3为实数,则正实数m的值为
A.1+2![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如三棱锥P—ABC的高PO=8,AC=BC=3,∠ACB=30°,M,N分别在BC和PO上,且CM=x,PN=2CM,试问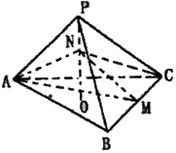 下面的四个图象中哪个图象大致描绘了三棱锥N—AMC的体积V与x的变化关系
下面的四个图象中哪个图象大致描绘了三棱锥N—AMC的体积V与x的变化关系![]()
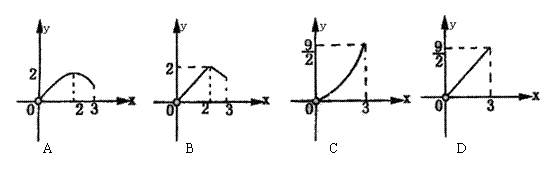 |
2006届浙江省乐清市柳市中学高三数学
理科模拟试卷(二)答题卷
第Ⅰ卷(选择题 共50分)
![]() 一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.把答案填写在对应方格内.
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.把答案填写在对应方格内.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷(非选择题 共100分)
注意事项:
1.第Ⅱ卷共4页,用钢笔或圆珠笔直接答在答题卷中.
2.答卷前将密封线内的项目填写清楚.
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在答卷中的横线上.
11.按ABO血型系统学说,每个人的血型为A,B,O,AB四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女一定不是O型,若某人的血型为O型,则父母血型所有可能情况有 种.
12.若(2x2-1)n的展开式中各项系数和为![]() 的展开式中各项系数和为
的展开式中各项系数和为![]() ,则
,则
![]() .
.
13.椭圆![]() 有相同的焦点,它们的一个公共点为
有相同的焦点,它们的一个公共点为![]() ,则
,则
b-a=
14.已知函数![]() (
(![]() ),下列命题中正确命题的序号为
),下列命题中正确命题的序号为
(1)![]() 必为偶函数;
必为偶函数;
(2)当![]() 时,
时,![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
(3)若![]() ,则
,则![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(4)![]() 的最大值为
的最大值为![]() .
.
三、解答题:(本大题共6小题,共84分,解答应写出文字说明,证明过程或演算步骤.)
15.(本小题满分14分)在△ABC中,![]() 求:
求:
(1)![]() 的值; (2)
的值; (2)![]() 的值.
的值.
16.(本题满分14分)已知函数![]() 问是否存在实数a、b使f(x)在
问是否存在实数a、b使f(x)在
[-1,2]上取得最大值3,最小值-29,若存在,求出a、b的值.并指出函数的单调区间 . 若不存在,请说明理由 .
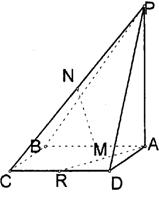
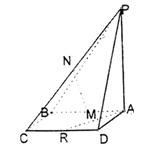
17.(本小题满分14分)已知:如图,矩形ABCD,PA⊥平面ABCD, M、N、R分别是AB、PC、CD的中点,
①求证:直线AR∥平面PMC ;
②求证:直线MN⊥直线AB ;
|
![]()
![]() 18.(本小题满分14分)银行按规定在一定时间结算利息一次,结息后即将利息并入本金,这种计算方法叫做复利,现在某企业进行技术改造,有两种方案;甲方案:一次性贷款10万元,第一年可获利1万元,以后每年比前一年增加30%的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元。两种方案的贷款使用期都是10年,到期一次性还本付息,若银行贷款利率是按年息10%的复利计算,试比较两种方案的优劣(计算时精确到千元,并取1.110
18.(本小题满分14分)银行按规定在一定时间结算利息一次,结息后即将利息并入本金,这种计算方法叫做复利,现在某企业进行技术改造,有两种方案;甲方案:一次性贷款10万元,第一年可获利1万元,以后每年比前一年增加30%的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元。两种方案的贷款使用期都是10年,到期一次性还本付息,若银行贷款利率是按年息10%的复利计算,试比较两种方案的优劣(计算时精确到千元,并取1.110![]() 2.594,1.310
2.594,1.310![]() 13.79).
13.79).
19.(本小题满分14分)
设数列{an}的前n项和为Sn ,且![]() 其中p为常数,且
其中p为常数,且![]() 。 ①求证:数列{an}是等比数列,并求出数列{an}的通项公式 ;
。 ①求证:数列{an}是等比数列,并求出数列{an}的通项公式 ;
②若数列{an}的公比![]() 求出数列
求出数列![]() 的通项公式;
的通项公式;
③在②的条件下,![]() 求实数
求实数![]() 的值;
的值;
④在③的条件下,又数列![]() 求无穷数列
求无穷数列![]() 的各项和.
的各项和.
20.(本小题满分14分)
若![]() 为双曲线
为双曲线![]() 的左,右焦点,
的左,右焦点,![]() 为坐标原点,
为坐标原点,![]() 在双曲线左支上,
在双曲线左支上,![]() 在右准线上,且满足
在右准线上,且满足![]() ,
,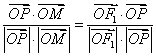 .
.
(1)求此双曲线的离心率;(2)若此双曲线过点![]() ,求双曲线方程;(3)设(2)中双曲线的虚轴端点为
,求双曲线方程;(3)设(2)中双曲线的虚轴端点为![]() 在
在![]() 轴正半轴上),点
轴正半轴上),点![]() 在双曲线上,且
在双曲线上,且![]() ,求
,求![]() 时,直线
时,直线![]() 的方程.
的方程.
参考答案
一、选择题
CDDCB AABBA
二、填空题
11. 9; 12.![]() ; 13.7; 14.③提示
; 13.7; 14.③提示![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调性不变.
单调性不变.
三、解答题
15.(1)![]() ,A为三角形的一个内角
,A为三角形的一个内角 ![]()
由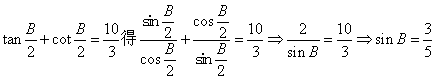
又![]()
∴![]() .
.
(2)由(1)和![]()
∴![]() .
.
16.解:![]() (舍2分)
(舍2分)
(1)a>0时,如下表
| x | (-1,0) | 0 | (0,2) |
|
| + | 0 | — |
|
|
| 最大值3 |
|
∴当x=0时,![]() 取得最大值, ∴b=3(6分)
取得最大值, ∴b=3(6分)
(2)a<0时,如下表
| x | (-1,0) | 0 | (0,2) |
|
| — | 0 | + |
|
|
| 最小值-29 |
|
∴当x=0时,![]() 取得最小值, ∴b=-29(9分) 又f(2)=-16a-29,
f(-1)=-7a-29<f(2)
取得最小值, ∴b=-29(9分) 又f(2)=-16a-29,
f(-1)=-7a-29<f(2)
|
综上:a=2, b=3 或a=-2, b=-29 (12分)
17.①连结CM,∵ABCD为矩形, CR=RD , BM=MA ,
∴CM∥AR, 又∵AR![]() 平面PMC,∴AR∥平面PMC(2分)
平面PMC,∴AR∥平面PMC(2分)
②连结MR、NR,在矩形ABCD中,AB⊥AD,PA⊥平面AC,
∴PA ⊥AB,AB⊥平面PAD,∵MR∥AD, NR∥PD,
∴面PDA∥平面NRM , ∴AB⊥平面NRM,则AB⊥MN(6分)
③PA⊥平面ABCD,∴AD为PD在平面ABCD上的射影,∵AD⊥CD由三垂线定理PD⊥CD ∴∠PDA是二面角P—CD—A的平面角, (6分)
∠ADC=θ,在Rt△PDA中,设AD=a
, PD=![]() ,MR∥PD,NR∥AD;要使MN是异面直线AB,PC的公垂线, ∴MN⊥PC 由②MN⊥AB, ∵CD∥AB,
,MR∥PD,NR∥AD;要使MN是异面直线AB,PC的公垂线, ∴MN⊥PC 由②MN⊥AB, ∵CD∥AB,
∴MN⊥CD, MN⊥平面PCD,∠MNR=90°,(10分)在Rt△MNR中,
2NR=PD=![]() ,MR=
,MR=![]()
![]() 时,能使直线MN是异面直线AB、PC的公垂线(12分)
时,能使直线MN是异面直线AB、PC的公垂线(12分)
18.甲方案:10年共获利42.63万元,银行贷款本息共25.94万元,净收益为16.7万元;
乙方案:10年共获利32.5万元,银行贷款本息共17.53万元,净收益为15.0万元; 所以,甲方案优于乙方案。
19.解:①![]() (1分)
(1分)
两式相减得![]() (2分)
(2分)
再由当n=1时,![]()
![]()
∴数列![]() 是以a1=1,为首项,以
是以a1=1,为首项,以![]() 为公比的等比数列
为公比的等比数列![]() (4分)
(4分)
|
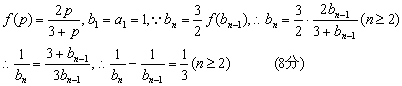
数列![]() 是以
是以![]() =1为首项,以
=1为首项,以![]() 为公差的等差数列
为公差的等差数列
![]() (9分)
(9分)
③![]()
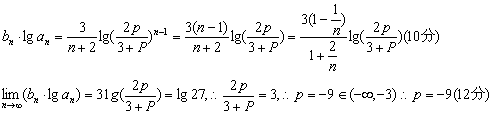
④![]() (14分)
(14分)
20.解:(1)由![]() 知四边形PF1OM为平行四边形,又由
知四边形PF1OM为平行四边形,又由![]()
知![]() 为菱形,设半焦距为c,由
为菱形,设半焦距为c,由![]() ,
,

![]()
(2)![]() 双曲线方程为
双曲线方程为![]() 代入,有
代入,有![]() 即所求双曲线方程为
即所求双曲线方程为![]()
(3)依题意得B1(0,3),B2(0,-3).![]() A、B2、B共线.
A、B2、B共线.
设直线AB的方程为![]()
则由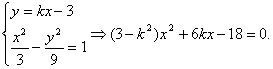
∵双曲线的渐近线为![]() 时,AB与双曲线只有一个交点,
时,AB与双曲线只有一个交点,
即![]()
![]()
![]()
又![]()
![]()
故所求直线AB的方程为![]()