2006中国数学奥林匹克
(第二十一届全国中学生数学冬令营)
第一天
福州
一、 实数![]() 满足
满足![]() ,求证:
,求证:
 .
.
证明
只需对任意![]() ,证明不等式成立即可.
,证明不等式成立即可.
记![]() ,则
,则
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
把上面这n个等式相加,并利用![]() 可得
可得
![]() .
.
由Cauchy 不等式可得
![]()
![]()
![]()
![]() ,
,
所以
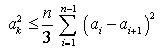 .
.
二、正整数![]() (可以有相同的)使得
(可以有相同的)使得![]() 两两不相等.问:
两两不相等.问:![]() 中最少有多少个不同的数?
中最少有多少个不同的数?
解 答案:![]() 中最少有46个互不相同的数.
中最少有46个互不相同的数.
由于45个互不相同的正整数两两比值至多有45×44+1=1981个,故![]() 中互不相同的数大于45.
中互不相同的数大于45.
下面构造一个例子,说明46是可以取到的.
设![]() 为46个互不相同的素数,构造
为46个互不相同的素数,构造![]() 如下:
如下:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
这2006个正整数满足要求.
所以![]() 中最少有46个互不相同的数.
中最少有46个互不相同的数.
三、正整数m,n,k满足:![]() ,证明不定方程
,证明不定方程
![]()
和
![]()
中至少有一个有奇数解![]() .
.
证明 首先我们证明如下一个
引理:不定方程
![]() ①
①
或有奇数解![]() ,或有满足
,或有满足
![]() ②
②
的偶数解![]() ,其中k是整数.
,其中k是整数.
引理的证明 考虑如下表示
![]()
![]()
![]() ,
,
则共有 个表示,因此存在整数
个表示,因此存在整数![]() ,
,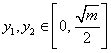 ,满足
,满足![]() ,且
,且
![]() ,
,
这表明
![]() ,
③
,
③
这里![]() 。由此可得
。由此可得
![]() ,
,
故![]() ,因为
,因为![]() ,所以
,所以
![]() ,
,
于是![]() .因为m为奇数,
.因为m为奇数,![]() ,
,![]() 显然没有整数解.
显然没有整数解.
(1)
若![]() ,则
,则![]() 是方程①满足②的解.
是方程①满足②的解.
(2)
若![]() ,则
,则![]() 是方程①满足②的解.
是方程①满足②的解.
(3)
若![]() ,则
,则![]() .
.
首先假设![]() m
m![]()
![]()
![]()
![]()
![]() ,且
,且![]()
![]()
![]() ,则
,则
![]() ④
④
是方程①满足②的解.若![]()
![]()
![]() ,则
,则
![]() ⑤
⑤
是方程①满足②的解.
现在假设![]() ,则公式④和⑤仍然给出方程①的整数解.若方程①有偶数解
,则公式④和⑤仍然给出方程①的整数解.若方程①有偶数解![]() ,则
,则
![]() .
.
因为![]() 的奇偶性不同,所以
的奇偶性不同,所以![]() ,
,![]() 都为奇数.
都为奇数.
若![]() ,则
,则![]() 是方程①的一奇数解.
是方程①的一奇数解.
若![]()
![]()
![]() ,则
,则![]() 是方程①的一奇数解.
是方程①的一奇数解.
(4)![]() ,则
,则![]() .
.
当![]() m
m![]() ,或
,或![]() ,则
,则
![]() ⑥
⑥
是方程①满足②的解.
若![]() ,或
,或![]() ,则
,则
![]() ⑦
⑦
是方程①满足②的解.
当![]() ,则公式⑥和⑦仍然给出方程①的整数解.若方程①有偶数解
,则公式⑥和⑦仍然给出方程①的整数解.若方程①有偶数解![]() ,则
,则
![]()
![]()
![]()
![]() ,
,
可得
![]() .
.
若 ![]() ,或者
,或者 ![]() ,或者
,或者
![]() ,则
,则![]() 是方程①的一奇数解.
是方程①的一奇数解.
若 ![]() ,或
,或![]() ,则
,则
![]()
是方程①的一奇数解.
引理证毕.
由引理,若方程①没有奇数解,则它有一个满足②的偶数解![]() .令
.令![]() ,考虑二次方程
,考虑二次方程
![]() ,
⑧
,
⑧
则
![]() ,
,
这表明方程⑧至少有一个整数根![]() ,即
,即
![]() , ⑨
, ⑨
上式表明![]() 必为奇数.将⑨乘以4n后配方得
必为奇数.将⑨乘以4n后配方得
![]() ,
,
这表明方程![]() 有奇数解
有奇数解![]() .
.
2006中国数学奥林匹克
(第二十一届全国中学生数学冬令营)
第二天
福州
四、在直角三角形ABC中,![]() ,△ABC 的内切圆O分
,△ABC 的内切圆O分
别与边BC,CA, AB 相切于点D,E,F,连接AD,与内切圆O相交于点P,连接BP,CP,若![]() ,求证:
,求证:![]() .
.
证明 设AE = AF = x,BD=BF=y,CD=CE=z,AP=m,PD=n.
因为![]() ,所以
,所以![]() .
.

延长AD至Q,使得![]() ,连接BQ,CQ,则P,B,Q,C四点共圆,令DQ=l,则由相交弦定理和切割线定理可得
,连接BQ,CQ,则P,B,Q,C四点共圆,令DQ=l,则由相交弦定理和切割线定理可得
![]() ,
①
,
①
![]() .
②
.
②
因为![]() ∽
∽![]() ,所以
,所以![]() ,故
,故
![]() .
③
.
③
在Rt △ACD和Rt △ACB中,由勾股定理得
![]() ,
④
,
④
![]() .
⑤
.
⑤
③-②,得
![]() ,
⑥
,
⑥
①÷⑥,得
![]() ,
,
所以
![]() ,
⑦
,
⑦
②×⑦,结合④,得 ![]() ,
,
整理得
![]() .
⑧
.
⑧
又⑤式可写为
![]() ,
⑨
,
⑨
由⑧,⑨得
![]() .
⑩
.
⑩
又⑤式还可写为
![]() ,
11
,
11
把上式代入⑩,消去![]() ,得
,得
![]() ,
,
解得
![]() ,
,
代入11得,
![]() ,
,
将上面的x,y代入④,得
![]() ,
,
结合②,得
![]() ,
,
从而
![]() ,
,
所以,![]() ,即
,即 ![]() .
.
五、实数列![]() 满足:
满足:![]() ,
,
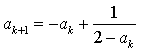 ,
,![]() .
.
证明不等式
 .
.
证明 首先,用数学归纳法证明:![]() .
.
![]() 时,命题显然成立.
时,命题显然成立.
假设命题对![]() 成立,即有
成立,即有![]() .
.
设![]() ,则
,则![]() 是减函数,于是
是减函数,于是
![]() ,
,
![]()
![]() ,
,
即命题对n+1也成立.
原命题等价于
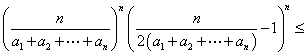
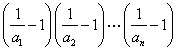 .
.
设![]() ,则
,则![]() 是凸函数,即对
是凸函数,即对![]() ,有
,有![]() .
.
事实上,![]() 等价于
等价于
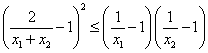 ,
,
![]() .
.
所以,由Jenson 不等式可得
![]() ,
,
即
 .
.
另一方面,由题设及Cauchy不等式,可得
![]()
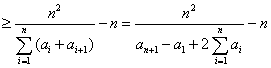
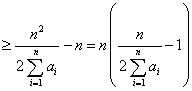 ,
,
所以
 ,
,
故

 ,
,
从而原命题得证.
六、设X是一个56元集合.求最小的正整数n,使得对X的任意15个子集,只要它们中任何7个的并的元素个数都不少于n,则这15个子集中一定存在3个,它们的交非空.
解 n的最小值为41.
首先证明![]() 合乎条件.用反证法.假定存在X的15个子集,它们中任何7个的并不少于41个元素,而任何3个的交都为空集.因每个元素至多属于2个子集,不妨设每个元素恰好属于2个子集(否则在一些子集中添加一些元素,上述条件仍然成立),由抽屉原理,必有一个子集,设为A,至少含有
合乎条件.用反证法.假定存在X的15个子集,它们中任何7个的并不少于41个元素,而任何3个的交都为空集.因每个元素至多属于2个子集,不妨设每个元素恰好属于2个子集(否则在一些子集中添加一些元素,上述条件仍然成立),由抽屉原理,必有一个子集,设为A,至少含有![]() =8个元素,又设其它14个子集为
=8个元素,又设其它14个子集为![]() .考察不含A的任何7个子集,都对应X中的41个元素,所有不含A的7-子集组一共至少对应
.考察不含A的任何7个子集,都对应X中的41个元素,所有不含A的7-子集组一共至少对应![]() 个元素.另一方面,对于元素a,若
个元素.另一方面,对于元素a,若![]() ,则
,则![]() 中有2个含有a,于是a被计算了
中有2个含有a,于是a被计算了![]() 次;若
次;若![]() ,则
,则![]() 中有一个含有a,于是a被计算了
中有一个含有a,于是a被计算了![]() 次,于是
次,于是
![]()
![]()
![]() ,
,
由此可得![]() ,矛盾.
,矛盾.
其次证明![]() .
.
用反证法.假定![]() ,设
,设![]() ,令
,令
![]() ,
,
![]() .
.
显然,![]() ,
,![]() ,
,![]() ,
,![]() ,于是,对其中任何3个子集,必有2个同时为
,于是,对其中任何3个子集,必有2个同时为![]() ,或者同时为
,或者同时为![]() ,其交为空集.
,其交为空集.
对其中任何7个子集![]() ,有
,有
![]()
![]()
![]()
![]() ,
,
任何3个子集的交为空集,所以![]() .
.
综上所述,n的最小值为41.