2006年黄冈市数学高考模拟试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共150分,考试时间120分钟。
第I卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。![]()
1.含有三个实数的集合可表示为{a, ![]() ,1},也可表示为{a
,1},也可表示为{a![]() ,a+b ,0},则a
,a+b ,0},则a![]() +b
+b![]() 的值为
的值为
A.0
B.1
C.—1
D.![]()
2.由下列各组命题构成“p或q”、“p且q”、“非p”形式的复合命题中,“p或q”为真,“p且q”为假,“非p”为真的是
A.p:3是偶数,q:4是奇数 B.p:3+2=6,q:5>3
|
|
3.
ABCD为正方形,PD![]() 平面ABCD,则二面角A-PB-C的大小范围是
平面ABCD,则二面角A-PB-C的大小范围是
A.(0![]() ,180
,180![]() ) B.(60
) B.(60![]() ,180
,180![]() ) C.[90
) C.[90![]() ,180
,180![]() ]
] ![]() D.(90
D.(90![]() ,180
,180![]() )
)
4.不等式x![]() +x+x
+x+x![]() +x
+x![]() <0的解集是
<0的解集是
A.![]() B.R
B.R![]() C.R
C.R![]()
![]() D.{xx
D.{xx![]() R且x
R且x![]() 0}
0}
5.设![]() ),且sin
),且sin![]() 等于
等于
A.![]() B.—
B.—![]() C.
C.![]() D.—
D.—![]() 或
或![]()
6.若能通过适当选择常数a、b,使lim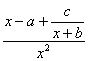 存在,则常数c是
存在,则常数c是
A.正数 B.零 C.负数 D.不能判断c的符号
7.如果![]() ~B(n,P),其中0<P<1,那么使P(
~B(n,P),其中0<P<1,那么使P(![]() =k)取最大值的k值
=k)取最大值的k值
A. 有且有1个 B.有且只有2个
C.不一定有 D.当(n+1)P为正整数时有2个
8.在等差数列{a![]() }中,3(a
}中,3(a![]() +a
+a![]() )+2(a
)+2(a![]() +a
+a![]() +a
+a![]() )=24,则此数列的前13项之和为
)=24,则此数列的前13项之和为
A.156 B.13 C.12 D.26
9.已知在![]() 中,
中,![]() ·
·![]() <0,S△ABC =
<0,S△ABC =![]() ,
,![]() =3,
=3,![]() =5,则
=5,则![]()
A.30![]() B.60
B.60![]() C.150
C.150![]() D.30
D.30![]() 或150
或150![]()
10.甲、乙分别将1000元按不同方式同时存入银行,甲采用的是一年期整存整取定期储蓄,年利率为2.25﹪,1年后将本利一并取出,并全部存入下一期这种定期储蓄,下一年仍存这种存款;乙采用的是3年期整存整取定期储蓄,年利率为2.70﹪,若1.0225![]()
![]() 1.069,则3年后两人所得的利息(不计利息税)
1.069,则3年后两人所得的利息(不计利息税)
A.相等 B.甲比乙多 C.甲比乙少12元 D.甲比乙少16.5元
11.已知f(x)=(x-a)(x-b)-2,并且![]() 是方程f(x)=0的两根,实数a、b、
是方程f(x)=0的两根,实数a、b、![]() 、
、![]() 的大小关系可能是
的大小关系可能是
A.![]() <a<b<
<a<b<![]() B.a<
B.a<![]() <
<![]() <b C.a<
<b C.a<![]() <b<
<b<![]() D.
D.![]() <a<
<a<![]() <b
<b
12.ABCD为四边形,动点p沿折线BCDA由点B向A点运动,设p点移动的路程为x,
△ABP的面积为S,函数S=f(x)的图象如图,给出以下命题:
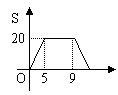 ①ABCD是梯形;
①ABCD是梯形;
②ABCD是平行四边形;
③若Q为AD的中点时,那么△ABQ面积为10;
④当9![]() x
x![]() 14时,函数S=f(x)的解析式为56-4x.
14时,函数S=f(x)的解析式为56-4x.
其中正确命题为
A.①② B.②③ C.②④ D.①③④
第II卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案直接填在题中横线上.
13.有15名新生,其中有3名优秀生,现随机将他们分到三个班级中去,每班5人,则每班都分到优秀生的概率是 .
14.给出下列命题:①若a,b共线,且 a = b ,则(a-b)//(a+b);②已知a=2e,b=3e,则a=![]() b;③若a=e
b;③若a=e![]() -e
-e![]() ,b=-3 e
,b=-3 e![]() +3 e
+3 e![]() ,且e
,且e![]()
![]() e
e![]() ,则 a =3 b ;④在△ABC中,AD是中线,则
,则 a =3 b ;④在△ABC中,AD是中线,则![]() =
=![]() =2
=2![]() .其中,正确命题的序号是
.
.其中,正确命题的序号是
.
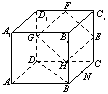 15.如图,在正四棱柱ABCD—A
15.如图,在正四棱柱ABCD—A![]() B
B![]() C
C![]() D
D![]() 中,E、F、G、H分别是棱CC
中,E、F、G、H分别是棱CC![]() 、C
、C![]() D
D![]() 、D
、D![]() D、DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,
D、DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,
则M满足条件 时,有MN//平面B![]() BDD
BDD![]() 。
。
16.已知点F![]() 、F
、F![]() 分别是双曲线
分别是双曲线![]() -
-![]() =1的左、右焦点,过F
=1的左、右焦点,过F![]() 且垂直于x轴的直线与双曲线交于A、B两点,若△ABF
且垂直于x轴的直线与双曲线交于A、B两点,若△ABF![]() 为锐角三角形,则该双曲线的离心率e的取值范围是 .
为锐角三角形,则该双曲线的离心率e的取值范围是 .
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)
|
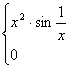
18.(本小题满分12分)
已知△ABC中, 三个内角A、B、C的对边分别是a、b、c,若△ABC的面积为S,且
2S=(a+b)2-c2,求tanC的值。
19.(本小题满分12分)
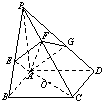
四棱锥P-ABCD中,底面是正方形,PA垂直于底面,过A的截面AEFG分别交PB、PC、PD于E、F、G,且PC![]() 截面AEFG。
截面AEFG。
(1)求证:点A、B、C、D、E、F、G在同一球面上;
(2)若PA=AB=1,求截面AEFG截(1)中的球的截面面积。
20.(本小题满分12分)
学校餐厅每天供应1000名学生用餐,每星期一有A、B两样菜可供选择,调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A![]() 、B
、B![]() 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)试以A![]() 表示A
表示A![]() ;(2)若A
;(2)若A![]() =200,求{A
=200,求{A![]() }的通项公式;
}的通项公式;
(3)问第n个星期一时,选A与选B的人数相等?
21.(本小题满分12分)
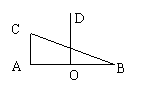
如图Rt△ABC中,![]() CAB=90
CAB=90![]() ,AB=2,AC=
,AB=2,AC=![]()
![]() ,DO
,DO![]() AB于O,OA=OB,DO=2,曲线E过C点,动点P在E上运动,且保持 PA
+ PB 的值不变。
AB于O,OA=OB,DO=2,曲线E过C点,动点P在E上运动,且保持 PA
+ PB 的值不变。
(1)建立适当的坐标系,求曲线E的方程;
 (2)过D点的直线l与曲线E相交于不同的两点M、N,且M在D、N之间,设
(2)过D点的直线l与曲线E相交于不同的两点M、N,且M在D、N之间,设![]() =
=![]() ,求
,求![]() 的取值范围。
的取值范围。
22.(本小题满分14分)
已知函数f(x)=![]() ,a
,a![]() R.
R.
(1)当x![]() [a+1,a+2]时,求f(x)的取值范围;
[a+1,a+2]时,求f(x)的取值范围;
(2)证明:函数y=f(x)的图象关于点(a,-1)成中心对称图形;
(3)我们利用函数y=f(x)构造一个数列{x![]() },方法如下:对于给定的定义域中的x
},方法如下:对于给定的定义域中的x![]() ,令x
,令x![]() =f(x
=f(x![]() ),x
),x![]() =f(x
=f(x![]() ),…,x
),…,x![]() =f(x
=f(x![]() -1),…
-1),…
在上述构造数列的过程中,如果x![]() (i=2,3,4,…)在定义域中,构造数列的过程将继续下去;如果x
(i=2,3,4,…)在定义域中,构造数列的过程将继续下去;如果x![]() 不在定义域中,则构造数列的过程停止。
不在定义域中,则构造数列的过程停止。
①如果可以用上述方法构造出一个常数列{x![]() },求实数a的取值范围;
},求实数a的取值范围;
②如果取定义域中任一值作为x![]() ,都可以用上述方法构造出一个无穷数列{x
,都可以用上述方法构造出一个无穷数列{x![]() },求实数a的值。
},求实数a的值。
2004黄冈市数学高考模拟试卷答案
1. C 2.B 3.D 4.A 5.C 6.A 7.D 8.D 9.C
10.C 11.A 12.D
13.![]()
![]() 14.①③④ 15.M
14.①③④ 15.M![]() 线段FH 16.(1,1+
线段FH 16.(1,1+![]() )
)
|
 =
=18.依题意,得absinC=a![]() +b
+b![]() -c
-c![]() +2ab。由余弦定理知:ab
+2ab。由余弦定理知:ab![]() -c
-c![]() =2abcosC。
=2abcosC。
![]() absinC=2ab(1+cosC),即sinC=2(1+cosC).
absinC=2ab(1+cosC),即sinC=2(1+cosC).
![]() sin
sin![]() cos
cos![]() =2cos
=2cos![]()
![]()
又0![]() <C<180
<C<180![]() ,
,![]() cos
cos![]()
![]() 0,
0,![]() sin
sin![]() =2cos
=2cos![]() ,即tan
,即tan![]() =2.
=2.
![]() tanC=
tanC= =
=![]() =-
=-![]() .
.
 19.如图,因为ABCD为正方形,PC
19.如图,因为ABCD为正方形,PC![]() 截面AEFG,则AF
截面AEFG,则AF![]() PC,利用
PC,利用
直径所对的圆周角是直角,猜想这个球的球心在正方形中心O,可知
A、B、C、D、F在以O为球心,![]() AC为半径的球面上,以下只需证
AC为半径的球面上,以下只需证
明G、E到O的距离也是![]() AC 即可。
AC 即可。
|
|
(2)因为PA=AB=1,所以r=![]() ,因为平面AEFG截球,由(1)知A、E、F、G在球面上,所以AEFG为截面圆上的四个点,又AG
,因为平面AEFG截球,由(1)知A、E、F、G在球面上,所以AEFG为截面圆上的四个点,又AG![]() 平面PCD,FG
平面PCD,FG![]() 平面PCD,因为PC=
平面PCD,因为PC=![]() ,所以AF=
,所以AF=![]() =
=![]() =
=![]() ,截面圆的面积S=
,截面圆的面积S=![]() (
(![]() )
)![]() =
=![]() 。
。
20.(1)依题意,得
 ①
①
将B![]() =1000-A
=1000-A![]() 代入①,得A
代入①,得A![]() =0.5A
=0.5A![]() +300 ②
+300 ②
(2)设A![]() +
+![]() =0.5(A
=0.5(A![]() +
+![]() ),即A
),即A![]() =0.5A
=0.5A![]() -0.5
-0.5![]() ,得-0.5
,得-0.5![]() =300,
=300,
![]()
![]() =-600.
=-600.![]() { A
{ A![]() -600}是以A
-600}是以A![]() -600=200-600=-400为首项,公比为0.5的等比数列。
-600=200-600=-400为首项,公比为0.5的等比数列。![]() A
A![]() -600=-400×0.5
-600=-400×0.5![]() ,
,![]() A
A![]() =600-400×0.5
=600-400×0.5![]() 。
。
(3)![]() A
A![]() = B
= B![]() ,且A
,且A![]() + B
+ B![]() =1000,
=1000,![]() A
A![]() =500,得600-400×0.5
=500,得600-400×0.5![]() =500。
=500。![]() 0.5
0.5![]() =0.5
=0.5![]() ,n-1=2,
,n-1=2,![]() n=3。即第三个星期一时,选A菜与选B菜的人数相等。
n=3。即第三个星期一时,选A菜与选B菜的人数相等。
21.(1)以AB、OD所在的直线分别为x轴、y轴,O为原点建立如图所示的直角坐标系。![]() PA + PB = CA + CB =
PA + PB = CA + CB =![]() +
+![]() =2
=2![]() ,所以动点的轨迹是椭圆,设其长、短半轴的长分别为a、b,半焦距为c,则a=
,所以动点的轨迹是椭圆,设其长、短半轴的长分别为a、b,半焦距为c,则a=![]() ,c=1,b=1,
,c=1,b=1,![]() 曲线E的方程为:
曲线E的方程为:![]() +y
+y![]() =1。
=1。
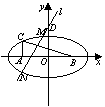 (2)设直线l的方程为y=kx+2,代入椭圆方程化简整理得:(2k
(2)设直线l的方程为y=kx+2,代入椭圆方程化简整理得:(2k![]() +1)x
+1)x![]() +8kx+6=0.设点M、N的坐标分别为(x
+8kx+6=0.设点M、N的坐标分别为(x![]() y
y![]() ),(x
),(x![]() y
y![]() ),则
),则
|
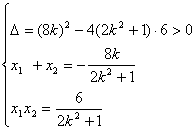
(i)当l与y轴重合时,![]() =
=![]() =
=![]() ;
;
(ii)当l与y轴不重合时,由①得k![]() >
>![]() ,又
,又![]()
![]() =
=![]() =
=![]() =
=![]() ,
,
![]() x
x![]() <x
<x![]() <0或x
<0或x![]() >x
>x![]() >0,
>0,![]() 0<
0<![]() <1
<1
![]()
![]() =
=![]() +
+![]() +2=
+2=![]() +
+![]() +2
+2
![]()
![]() =
=![]() =
= ,而k
,而k![]() >
>![]() ,
,![]() 6<3(2+
6<3(2+![]() )<8,
)<8,![]() 4<
4< <
<![]() ,由4<
,由4<![]() +
+![]() +2<
+2<![]() 得
得
2<![]() +
+![]() <
<![]() ,
,![]()
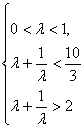 解得
解得![]() <
<![]() <1,
<1,
综合(i)(ii)得![]() 的取值范围为[
的取值范围为[![]() ,1
,1![]() 。
。
22.![]() f(x)=-1-
f(x)=-1-![]() 在[a+1,a+2]上是增函数,又f (a+1)=-2,f (a+2)=-
在[a+1,a+2]上是增函数,又f (a+1)=-2,f (a+2)=-![]() ,
,
![]() f
(x)
f
(x)![]() [-2,-
[-2,-![]() ]
]
(2)证明:设点P(x![]() ,y
,y![]() )是函数y=f (x)图象上任一点,则y
)是函数y=f (x)图象上任一点,则y![]() =-1-
=-1-![]() ,点P关于点(a,-1)的对称点为P(2a-x
,点P关于点(a,-1)的对称点为P(2a-x![]() ,-2-y
,-2-y![]() ).
).
![]() f (2a-x
f (2a-x![]() )=-1-
)=-1-![]()
![]() f
(2a-x
f
(2a-x![]() )=-2-y
)=-2-y![]() ,即点P
,即点P![]()
![]() 在函数y=f (x)的图象上,所以函数y=f (x)的图象关于点(a,-1)成中心对称图形。
在函数y=f (x)的图象上,所以函数y=f (x)的图象关于点(a,-1)成中心对称图形。
(3)①根据题意,只需x![]() a时,f(x)=x有解,即
a时,f(x)=x有解,即![]() 有解,即x
有解,即x![]() +(1-a)x+1-a=0有不等于a的解。
+(1-a)x+1-a=0有不等于a的解。
将x=a代入方程左边,得左边=1,故方程不可能有解x=a。
由△![]() 0时,得a
0时,得a![]() -3或a
-3或a![]() 1,即为所求实数a的取值范围。
1,即为所求实数a的取值范围。
②根据题意,![]() 在R中无解,即x
在R中无解,即x![]() a时,(1+a)x=a
a时,(1+a)x=a![]() +a-1无解。
+a-1无解。
由于x=a不是方程(1+a)x= a![]() +a-1的解,所以对于任意x
+a-1的解,所以对于任意x![]() R,(1+a)x= a
R,(1+a)x= a![]() +a-1无解。
+a-1无解。
![]() a=-1,即为所求a有值。
a=-1,即为所求a有值。