.
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
(1)集合A＝｛１，２，３｝，Ｂ＝｛－１，０，１｝，满足条件f(3)=f(1)+f(2)的
映射f:A→B的个数是D
(A)2 (B)4 (C)5 (D)7
(2)设向量
对应的复数为z=1+i，它的辐角主值为θ，将向量按顺时针方向
绕原点O旋转2θ，得向量
，则向量
对应的复数为C
(A)－１＋ｉ (B)１－ｉ (C)－２ｉ (D)２ｉ
(3)函数
在其定义域上是B
(A)奇函数，增函数 (B)奇函数，减函数
(C)奇函数，没有单调性 (D)减函数，没有奇偶性
(4)双曲线
（ａ＞０，ｂ＞０）的渐近线与x轴的夹角为α（０＜α＜
＝，
则过双曲线的焦点且垂直于x轴的弦的长度为D
(A)ａｔｇα (B)ｂｔｇα (C)２ａｔｇα (D)２ｂｔｇα
(5)无盖的圆柱形容器的底面半径为
，母线为3，现将盛水的该容器平稳地缓慢倾斜，
当水剩到原来的
时，圆柱的母线与水平面所成的角α∈C
(A)（０，
） (B)（，
） (C)（，
） (D)（，）
(6)设函数
α、β为锐角，如果对任何x＞０，都有f(x)＜２，那么D
(A)０＜α＋β＜ (B)０＜α＋β＜ (C) ＜α＋β＜ (D)α＋β＞
(7)函数y=ａｒｃｃｏｓ（ａｘ－１）在x∈［０，１］时是减函数，则实数a的取值范围是D
（A）［１，＋∞］ (B)（０，＋∞） (C)（０，１） (D)（０，２）
(8)上、下两个底面平行且都是长方形，四个侧面都是全等的等腰梯形的六面体D
(A)是不存在的 (B)是正四棱台
(C)是四棱台但可能不是正四棱台 (D)存在但可能不是正棱台
(9)四面体的顶点和各棱中点共10个点，其两两连线可组成异面直线的对数为B
(A)83 (B)87 (C)91 (D)95
(10)在直线x –y =0与y ＝０上分别有一点M，N，使点M、N和点A(3，1)满足
｜ＡＭ｜＋｜ＭＮ｜＋｜ＮＡ｜有最小值时，点M、N的坐标分别是B
(A)（
），（
，０） (B)（
），（，０）
(C)（１，３），（２，０） (D)（），（０，）
(11)如图，在一个盛了水的圆柱形容器内，其水面以下有一个用细线吊着的下端开了很小的孔、充满水的薄壁小球，当慢慢地匀速地将小球从水下向水面以上拉动时，柱形容器内水面的高度h与时间t的函数图象大致是D
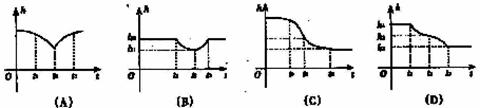
(12)设a、b是方程x２＋ｃｔｇθ·ｘ－ｃｏｓθ＝０的两个不等实根，那么过点
A(a,a２)和B(b,b２)的直线与圆x２＋ｙ２＝１的位置关系是C
(A)相离 (B)相切 (C)相交 (D)随θ的值变化而变化
二、、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
(13)将一个三棱锥和一个三棱柱接成一个多面体，这个多面体的面数最少可达到 5 ．
(14)设正实数a、b、c、d满足(a-1)(b-1)＜０＜(a-1)（ｃ－１），
且ｌｏｇｄａ＋ｌｏｇｄｂ＝ｌｏｇｄｃ，则｜ｌｏｇｄａ｜与｜ｌｏｇｄｂ｜
的大小关系为 logda>logdb .
(15)在一支长15厘米，粗细均匀的圆柱形蜡烛的下端固定一个薄金属片(体积不计)，使蜡烛恰好能竖直地浮于水中，上端有1厘米高的部分露在水面上，已知蜡烛比重为0.85
克／立方厘米，现在点燃蜡烛，当蜡烛被水淹没时，它的剩余长度是 6.67厘米 .
(16)设有四个条件：
① 平面γ与平面α、β所成的锐二面角相等；
② 直线a∥b,a⊥平面α，b⊥β；
③ a、b是异面直线，
，且ａ∥β，ｂ∥α；
④ 平面α内距离为d的两条直线在平面β内的射影仍为两条距离为d的平行线，其中能推出α∥β的条件有 (2) (3) .(填写所有正确条件的代号)
答案
1、D . 2、C . 3、B . 4、D . 5、C . 6、D . 7、D . 8、D . 9、B . 10、B .
11、D . 12、C .
13、5 . 14、logda>logdb . 15、6.67厘米 . 16、(2) (3) .