一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)设集合Ａ＝｛ｘ｜－１≤ｘ≤１｝，Ｂ＝｛ｙ｜１≤ｙ≤２｝，下列图中，能表示从集合A到集合B的映射的是D

(2)将复数－１＋ｉ对应的向量顺时针方向旋转160°得到向量，则对应的复数的辐角主值为 C

　 (Ａ)１１５°　 (Ｂ)２９５°　　(Ｃ)３３５°　　(Ｄ)－２５°

(3)若函数y=f(x)的反函数的图象过点(２，－１)，则此函数可能是B

 (Ａ)ｙ＝２^ｘ　　(Ｂ)ｙ＝（）^ｘ (Ｃ)ｙ＝３^ｘ　　　 (Ｄ)ｙ＝１０^ｘ

(4)将函数y=f(x)·ｃｏｓｘ的图象向右平移个单位，再把所得图象向上平移1个单位，得到函数ｙ＝２ｓｉｎ^２ｘ的图象，那么函数f(x)可以是　D

 (Ａ)ｃｏｓｘ　　　 (Ｂ)２ｃｏｓｘ　　 (Ｃ)ｓｉｎｘ　(Ｄ)２ｓｉｎｘ

(5)正方形纸片ABCD，沿对角线AC对折，使D点在面ABC外，这时DB与面ABC所成的

角一定不等于D

 (Ａ)３０°　　(Ｂ)４５°　　(Ｃ)６０°　　(Ｄ)９０°

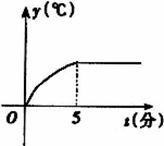
(6)在某种金属材料的耐高温实验中，温度随着时间变化的情况由微机记录后显示出的图象如右图所示，现给出下面说法 ①前5分钟温度增加的速度越来越快　②前5分钟温度增加的速度越来越慢　③5分钟以后温度保持匀速增加　④5分钟以后温度保持不变，其中正确的说法是B

(Ａ)①与④　　(B)②与④　 (C)②与③　　　　　(D)①与③

(7)在等差数列｛ａ_ｎ｝中，若ａ_１０＝０，则有等式ａ_１＋ａ_２＋…＋ａ_ｎ＝ａ_１＋ａ_２＋…＋ａ_１９－ｎ（ｎ＜１９，ｎ∈Ｎ）成立.类比上述性质，相应地在等比数列｛ｂ_ｎ｝中，若ｂ_９＝１，则成立的等式是A

　(Ａ)∈N）

　(Ｂ) ∈Ｎ）

(Ｃ) ∈Ｎ）

　(Ｄ) ∈Ｎ）

(8)在极坐标系中，两圆方程分别为ρ^２－２ρｃｏｓθ＋２＝０，ρ＝２ｓｉｎθ，它们的位置关系是B

 (Ａ)相离　　　 (B)外切　　　 (C)相交　　　　 (D)内切

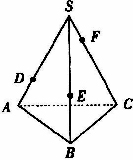
(9)如图，一个盛满水的三棱锥容器，不久发现三条侧棱上各有一个小洞D、E、F，且知SD∶ＤＡ＝ＳＥ∶ＥＢ＝ＣＦ∶ＦＳ＝２∶１，若仍用这容器盛水，则最多可盛原来水的B

 (Ａ)　　　 （B）　　  (Ｃ) 　　　　(D)

(10)已知抛物线ｙ＝ｘ^２－１上一定点Ａ（－１，０）和两动点P、Q，当ＰＡ⊥ＰＱ时，点Q的横坐标的取值范围是D

(Ａ)（－∞，－３）　　　　  (Ｂ)［１，＋∞］

(Ｃ)（－３，１）　　　　　  (Ｄ)（－∞，－３）∪［１，＋∞］

(11)设点P为异面直线a、b外的任意一点，若a与b所成的角为n度，且过P点恰有三

条直线a、b均成n度，则n的所有可能值有B

 (Ａ)０个　 　 (B)1个　　　　  (C)2个　　　　(D)无数多个

(12)有一件商品的成本为1000元，若在月初出售，可获利100元，然后将本利存入银行(已知银行月息为2%)；若在下月初出售，可获利120元，但要付5元保管费，则A

 (Ａ)本月初出售获利大　　　　 (B)在下月初出售获利大

(C)在本月初出售和在下月初出售获利相同

(D)在本月初出售和在下月初出售获利大小不能确定

二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.

(13)从集合｛０，１，２，－３，－５｝中任取3个元素，分别作为直线方程Ａｘ＋

Ｂｙ＋Ｃ＝０中的A、B、C，若所得直线的倾斜角不大于，则这样的直线共有　48　 条.

(14)若双曲线的右准线与抛物线ｙ^２－ｍｘ－２ｙ＋４ｍ＋１＝０的准线重合，则m =　　4　　　　　 .

(15)已知｛ａ_ｎ｝是等比数列，且ａ_２＞ａ_３＝１，则使不等式（ａ_１－）＋（ａ_２－）

＋…＋（ａ_ｎ－）＞０成立的自然数n的最大值是　　 4　　 .

(16)三棱锥Ｓ—ＡＢＣ对于以下条件 ①各侧面是等腰三角形且底面是正三角形　②底面是正三角形　③各侧面是正三角形　④顶点在底面的射影是底面三角形的外心.其中作为三棱锥S—ABC构成正三棱锥的必要不充分条件的是　　 (2) (4)　　　　　 .