一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)已知cosθ＝cos60°，则θ等于C

(A)60° (B)k·360°＋60°(k∈Z)  (C)k·360°±60°(k∈Z)  (D)k·180°＋60°(k∈Z)

(2)设全集I＝Ｒ，集合M＝｛x｜ｙ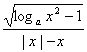＝，a＞1｝，则等于B

(A)(－∞，－)　　 (B)［－，＋∞ ）　　(C)(－,+∞)　　　 (D)(－∞,  )

(3)如果圆柱的母线长为4，侧面积为8π,那么它的轴截面的一条对角线的长度为C

(A)　　　　　　  (B) 　　　　　 (C)2 　　　　　　　 (D)4

(4)在极坐标系中，经过极点，且与直线ρcosθ=2切于点M(2，)的圆的方程是D

(A)ρ=4sinθ　　　　(B)ρ=2cosθ　　　 (C)ρ=－2cosθ　　　 (D)ρ=－4sinθ

(5)ω是正实数，函数f(x)=2sinωx在［－，］上递增，那么A

(A)0＜ω≤　　　 (B)0＜ω≤2　　　　(C)0＜ω≤ 　　　(D)ω≥2

(6)如果把直线x－2y+λ=0先向左平移1个单位，再向下平移2个单位，使其

与圆x²+y²+2x－4y=0相切，则实数λ的值是A

(A)3，13　　　　　  (B)－3，13　　　　 (C)3，－13　　　　　 (D)－3，－13

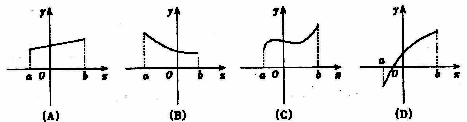
(7)任取x₁、x₂∈［a,b］且x₁≠x₂，若f()＞［f(x₁)+f(x₂)］,则f(x)在［a,b］上是上凸函数，在以下图象中，是上凸函数的图象是D

(8)已知函数f(x)=2arcsin(cosx)的定义域为(－，)，则f(x)的值域是A

(A)(－,π)　　　　 (B)(－,π)　 　 (C)(－) 　　　(D)( )

 (9)已知k∈N,则的值是D　 (A) 　 (B) 　　(C)2　　(D)1

(10)α、β是两个不同的平面，m、n是平面α及β外的两条不同直线，给出四个论断：①m⊥n;②α⊥β;③n⊥β;④m⊥α,以其中三个结论作为条件，另一个论断作为结论，则所得命题正确的个数是B

(A)1　　　　  (B)2　　　　　　 (C)3　　　　　　 (D)4

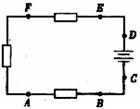
 (11)如图，某电子器件是由三个电阻组成的回路，其中共有六个焊接点A、B、C、D、E、F，如果某个焊接点脱落，整个电路就会不通，现在发现电路不通了，那么焊接点脱落的可能性共有A

(A)63种  　(B)64种　　　(C)6种　　 (D)36种

(12)设F₁(－c,0)、F₂(c,0)是椭圆=1(a＞b＞0)的两个焦点，P是以F₁F₂为直径的圆与椭圆的一个交点，若∠ＰＦ₁Ｆ₂＝5∠ＰＦ₂Ｆ₁，则椭圆的离心率为B

(A)　　　　　　  (B) 　　　　　 (C) 　　　　　　 (D)

二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.

(13)对于给定的二个数3和3x，它们的等差中项a与等比中项b之间满足条件3a²＝4b²，则正数b＝　　 或　　　　.

(14)设圆台的底面半径分别为1cｍ和7cｍ，如果该圆台的一个轴截面的两条对角线互相垂直，则这个圆台的侧面积为　　　80π　　 .

　(15)已知抛物线y²＝2ｐx(ｐ＞0)，过焦点F的直线交抛物线于A、B两点，线段AB的中点为P，抛物线的准线为l，分别过A、B、P作x轴的平行线依次交l于M、N、Q，连FM、FN、FQ、AQ和BQ，则这些线段中互相垂直的有　AQ⊥BQ、BQ⊥NF、AQ⊥MF　　　　　 .(至少找出三对)

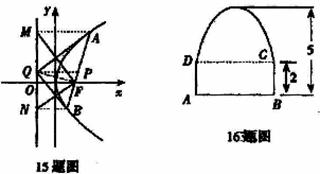
(16)设计一条单向行驶的公路隧道，需保证装有集装箱的汽车能够通过，如图所示隧道横断面由一段抛物线和矩形ABCD的三边组成，隧道高为5ｍ，BC＝2ｍ，装有集装箱的汽车高4ｍ，宽3ｍ，不考虑其他因素，隧道底部的宽AB应至少设计为　5.2　　　　 ｍ.(精确到0.1ｍ)