湖南省示范性高中2006届高三八校4月联考
数学(理科)测试试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟。
参考公式: 正棱锥、圆锥的侧面积公式
如果事件A、B互斥,那么
![]()
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中,c表示底面周长、l表示斜高或
P(A·B)=P(A)·P(B) 母线长
如果事件A在1次实验中发生的概率是 球的体积公式
P,那么n次独立重复实验中恰好发生k
![]()
次的概率 其中R表示球的半径
![]()
第I卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.
1.复数![]() 所对应的点在
所对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.函数![]() 的定义域为
的定义域为
A.![]() B.
B.![]() C.(1,+∞)
D.
C.(1,+∞)
D.![]()
3.已知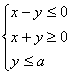 ,且
,且![]() 的最大值是3,则
的最大值是3,则![]() 的值为
的值为
A.1 B.-1 C.0 D.2
4.已知![]() ,
,![]() ,
,![]() 则向量
则向量![]() 与向量
与向量![]() 的夹角是
的夹角是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.某学校有高一学生720人,现从高一、高二、高三这三个年级学生中采用分层抽样的方
法,抽取180人进行英语水平测试.已知抽取的高一学生数是抽取的高二学生数、高三
学生数的等差中项,且高二年级抽取40人,则该校高三学生人数是
A.480 B.640 C.800 D.960
6.若![]() 是两个不重合的平面,
是两个不重合的平面,![]() 是两条不重合的直线,现给出下列四个命题:
是两条不重合的直线,现给出下列四个命题:
①若![]() 则
则![]() ; ②若
; ②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]() .
.
其中正确的命题是
A.①② B.②④ C.③④ D.②③④
7.数列![]() 的前100项的和等于
的前100项的和等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.命题甲:函数![]() 图象的一条对称轴方程是
图象的一条对称轴方程是![]() ;命题乙:直线
;命题乙:直线
![]() 的倾斜角为
的倾斜角为 ![]() ,则
,则
A.甲是乙的充分条件 B.甲是乙的必要条件
 C.甲是乙的充要条件 D.甲是乙的不充分也不必要条件
C.甲是乙的充要条件 D.甲是乙的不充分也不必要条件
9.如图过抛物线![]() 焦点的直线依次交抛
焦点的直线依次交抛
物线与圆![]() 于A,B,C,D,
于A,B,C,D,
则![]() =
=
A.4 B.2
C.1 D.![]()
10.函数![]() 在区间(
在区间(![]() ,1)上有最小值,则函数
,1)上有最小值,则函数![]() 在区间(1,
在区间(1,![]() 上一定
上一定
A.有最小值 B.有最大值 C.是减函数 D.是增函数
二.填空题:本大题共5小题,每小题4分,共20分,把答案填在题中横线上.
11.设全集为实数集R,若集合![]() ,则集合
,则集合![]() 等于
.
等于
.
 12.
12.![]() 展开式的常数项为
.
展开式的常数项为
.
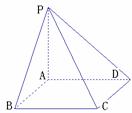
13.如图,已知PA⊥平面ABCD,四边形ABCD是正方形,
且PA=AD,则PB与AC所成的角的大小为 .
|
|
|
|
|
| 4 |
|
|
|
|
|
14.将1,2,3,……,9这九个数字填在如图所示
的9个空格中,要求每一行从左到右依次增大,
每一列从上到下也依次增大,数字4固定在中
心位置时,则所有填空格的方法有 种.
15.在一张纸上画一个圆,圆心为O,并在圆O外设置一个定点F,折叠纸片使圆周上某一
点与F点重合,设这一点为M,抹平纸片得一折痕AB,连MO并延长交AB于P.当
点![]() 在圆
在圆![]() 上运动时,则(i)P的轨迹是
;(ii)直线AB与该轨迹的公共点的个数是
.
上运动时,则(i)P的轨迹是
;(ii)直线AB与该轨迹的公共点的个数是
.
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
乒乓球世锦赛决赛,由马琳对王励勤,实行“五局三胜”制进行决赛,在之前比赛中马琳每一局获胜的概率为![]() ,决赛第一局王励勤获得了胜利,求:
,决赛第一局王励勤获得了胜利,求:
(1)马琳在此情况下获胜的概率;
(2)设比赛局数为![]() ,求
,求![]() 的分布及E
的分布及E![]() .
.
17.(本小题满分12分)
已知函数![]() ,
,![]() ,且函数
,且函数![]() 的图象是函数
的图象是函数![]() 的图象按向量
的图象按向量![]() 平移得到的.
平移得到的.
(1)求实数![]() 的值;
的值;
(2)设![]() ,求
,求![]() 的最小值及相应的
的最小值及相应的![]() .
.
18.(本小题满分14分)
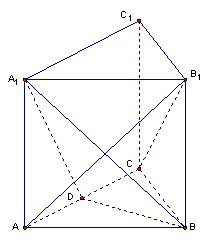 如图,正三棱柱ABC一A1B1C1的底面边长是2,侧棱长是
如图,正三棱柱ABC一A1B1C1的底面边长是2,侧棱长是![]() ,D为AC的中点.
,D为AC的中点.
(1)求证:B1C//平面A1BD;
(2)求二面角A1一BD一A的大小;
(3)求异面直线AB1与BD之间的距离.
19.(本小题满分14分)
![]() 是正数数列
是正数数列![]() 的前n项的和,数列S12,S22、……、Sn2 ……是以3为首项,以1为公差的等差数列;数列
的前n项的和,数列S12,S22、……、Sn2 ……是以3为首项,以1为公差的等差数列;数列![]() 为无穷等比数列,其前四项的和为120,第二项与第四项的和为90.
为无穷等比数列,其前四项的和为120,第二项与第四项的和为90.
(1)求![]() ;
;
(2)从数列{![]() }中依次取出部分项组成一个无穷等比数列
}中依次取出部分项组成一个无穷等比数列![]() ,使其各项和等于
,使其各项和等于![]() ,求数列
,求数列![]() 公比
公比![]() 的值.
的值.
20.(本小题满分14分)
已知函数![]() (
(![]() 为实数).
为实数).
(1)若![]() 在[-3,-2 )上是增函数,求实数
在[-3,-2 )上是增函数,求实数![]() 的取值范围;
的取值范围;
(2)设![]() 的导函数
的导函数![]() 满足
满足![]() ,求出
,求出![]() 的值.
的值.
21.(本小题满分14分)
已知双曲线C的中心在原点,对称轴为坐标轴,其一条渐近线方程是![]() ,且双曲线C过点
,且双曲线C过点![]() .
.
(1)求此双曲线C的方程;
(2)设直线L过点A(0,1),其方向向量为![]() (
(![]() >0),令向量
>0),令向量![]() 满足
满足![]() .问:双曲线C的右支上是否存在唯一一点B,使得
.问:双曲线C的右支上是否存在唯一一点B,使得![]() .若存在,求出对应的
.若存在,求出对应的![]() 的值和B的坐标;若不存在,说明理由.
的值和B的坐标;若不存在,说明理由.
数学试题(理科)答案
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.
1.D 2.B 3.A 4.C 5.D 6.D 7.A 8.A 9.C 10.D
二.填空题:本大题共5小题,每小题4分,共20分,把答案填在题中横线上.
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() 15
15![]()
16.(本小题满分12分)
解:(1)马胜出有两种情况3:1 或3:2,
则马胜的概率为![]() . ……………………………… 6分
. ……………………………… 6分
(2)![]() ,
,![]() , ………………… 8分
, ………………… 8分
![]() ,………………………………………………10分
,………………………………………………10分
所以分布列如下:
|
| 3 | 4 | 5 |
| P |
|
|
|
……………………………………………………………………………………………12分
17.(本小题满分12分)
解:(1)因为![]() ,
,
![]() ,
,
所以![]() .…………………………………………………………………………6分
.…………………………………………………………………………6分
(2)因为![]()
![]() ,
,
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() . ……………………12分
. ……………………12分
18.(本小题满分14分)
解:(1)证明(略) …………………………………………………………………… 4分
(2)![]() …………………………………………………………………………… 9分
…………………………………………………………………………… 9分
(3)![]() ……………………………………………………………………………14分
……………………………………………………………………………14分
19.(本小题满分14分)
解:(1){Sn}是以3为首项,以1为公差的等差数列;所以Sn2=3+(n–1)=n+2
因为an>0,所以Sn=![]() (nÎN). ………………………………………………… 2分
(nÎN). ………………………………………………… 2分
当n≥2时,an=Sn–Sn–1=![]() –
–![]() 又a1=S1=
又a1=S1=![]() ,
,
所以an= (nÎN).…………………………………………… 4分
(nÎN).…………………………………………… 4分
设{bn}的首项为b1,公比为q,则有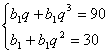 , ………………………… 6分
, ………………………… 6分
所以![]() ,所以bn=3n(nÎN). …………………………………………………… 8分
,所以bn=3n(nÎN). …………………………………………………… 8分
(2)由(1)得![]() =(
=(![]() )n,设无穷等比数列{cn}首项为c1=(
)n,设无穷等比数列{cn}首项为c1=(![]() )p,公比为(
)p,公比为(![]() )k,(p、kÎN),
)k,(p、kÎN),
它的各项和等于![]() =
=![]() , ……………………………………………………………10分
, ……………………………………………………………10分
则有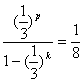 ,所以(
,所以(![]() )p=
)p=![]() [1–(
[1–(![]() )k], ………………………………………11分
)k], ………………………………………11分
当p≥k时3p–3p–k=8,即3p–k(3k–1)=8, 因为p、kÎN,所以只有p–k=0,k=2时,
即p=k=2时,数列{cn}的各项和为![]() . ……………………………………………12分
. ……………………………………………12分
当p<k时,3k–1=8.3k–p,因为k>p右边含有3的因数,
而左边非3的倍数,所以不存在p、kÎN,
综合以上得数列![]() 公比
公比![]() 的值为
的值为![]() .………………………………………………14分
.………………………………………………14分
20.(本小题满分14分)
解:(1)由题意得![]() 0对一切
0对一切![]() ∈[-3,-2 )恒成立,
∈[-3,-2 )恒成立,
即2![]() -
-![]() 0对一切
0对一切![]() ∈[-3,-2 )恒成立. ………………………………… 2分
∈[-3,-2 )恒成立. ………………………………… 2分
∴2![]()
![]() ,
,
![]() =
=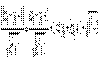 ,…………………………………… 4分
,…………………………………… 4分
当![]() ∈[-3,-2 )时, -(
∈[-3,-2 )时, -(![]() -
-![]() )2+
)2+![]() <-(2-
<-(2-![]() )2+
)2+![]() =-6,
=-6,
∴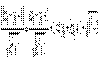 >-
>-![]() . …………………………………………………… 6分
. …………………………………………………… 6分
∴![]() ,所以
,所以![]() 的取值范围是(-∞,-
的取值范围是(-∞,-![]() ].
…………………………………
7分
].
…………………………………
7分
(2)因为![]() =2
=2![]() -[2
-[2![]() (1-
(1-![]() )+
)+
![]() ],
],
当![]() 时,则
时,则![]() 为单调递减函数,没有最大值. ……………………………
9分
为单调递减函数,没有最大值. ……………………………
9分
当![]() >0时, ∵
>0时, ∵![]() <1 ∴2
<1 ∴2![]() (1-
(1-![]() )>0
,
)>0
,![]() >0,
>0,
∴![]() . ………………………………………………………………11分
. ………………………………………………………………11分
由2![]() (1-
(1-![]() )+
)+
![]() 得
得![]() =1
=1![]()
![]() 由于
由于![]() =1+
=1+![]() >1,舍去.
>1,舍去.
所以当![]() =1-
=1-![]() 时,
时,![]() .……………………………………13分
.……………………………………13分
令2![]() -2
-2![]() =1-2
=1-2![]() ,解得
,解得![]() =
=![]() 或
或![]() =
=![]() -2
-2![]() ,即为所求. …………………14分
,即为所求. …………………14分
21.(本小题满分14分)
解:(1)依题意设双曲线C的方程为:![]() ,点P代入得
,点P代入得![]() .
.
所以双曲线C 的方程是![]() .……………………………………………… 4分
.……………………………………………… 4分
(2)依题意,直线![]() 的方程为
的方程为![]() (
(![]() ), ……………………………… 5分
), ……………………………… 5分
设![]() 为双曲线
为双曲线![]() 右支上满足
右支上满足![]() 的点,
的点,
则![]() 到直线
到直线![]() 的距离等于1,即
的距离等于1,即![]() .……………………… 6分
.……………………… 6分
①若![]() ,则直线
,则直线![]() 与双曲线
与双曲线![]() 右支相交,
右支相交,
故双曲线![]() 的右支上有两个点到直线
的右支上有两个点到直线![]() 的距离等于1,与题意矛盾.……………… 8分
的距离等于1,与题意矛盾.……………… 8分
②若![]() (如图所示),则直线
(如图所示),则直线![]() 在双曲线
在双曲线![]() 的右支的上方,故
的右支的上方,故![]() ,
,
从而有![]() .
.
又因为![]() ,所以有
,所以有![]() ,
,
整理,得![]() .……(★) ………10分
.……(★) ………10分
(i)若![]() ,则由(★)得
,则由(★)得![]() ,
,![]() ,
,
即![]() . ……………………………………………………………………………12分
. ……………………………………………………………………………12分
(ii)若![]() ,则方程(★)必有相等的两个实数根,故由
,则方程(★)必有相等的两个实数根,故由
![]() ,
,
解之得![]() (
(![]() 不合题意,舍去),此时有
不合题意,舍去),此时有
![]() ,
,![]() ,即
,即![]() .
.
综上所述,符合条件的![]() 的值有两个:
的值有两个:
![]() ,此时
,此时![]() ;
;![]() ,此时
,此时![]() . ………………………………14分
. ………………………………14分