08届高考理科数学第二次调研考试
理 科 数 学 试 卷
命题学校:宜都一中 命题教师:吴家强
考试时间: 2008年3月12日 15:00 -------17:00
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的4个选项中,只有一项是符合题目要求的,请将正确的选项填写到答题卷相应位置)
 1、设全集
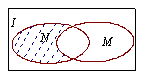
1、设全集![]() ,如图:
,如图:
则图中阴影部分所表示的集合为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、已知![]() ,且
,且![]() ,那么
,那么![]() 的值等于( )
的值等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、设i为虚数单位,则![]() 展开式中的第三项为( )
展开式中的第三项为( )
A.![]() B.
B.![]() C.6 D.
C.6 D. ![]()
4、已知l、m为两条直线,![]() 、
、![]() 是两个平面,则下列命题中的假命题是( )
是两个平面,则下列命题中的假命题是( )
A.若![]() ,
,![]() ,则
,则![]() B.若
B.若![]() ,
,![]() ,则
,则![]()
C.若![]() ,
,![]() ,则
,则![]() D. 若
D. 若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]()
5、若![]() 与
与![]() 都是非零向量,则“
都是非零向量,则“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分与不必要条件
6、已知点![]() ,B为椭圆
,B为椭圆![]() +
+![]() =1
=1![]() 的左准线与
的左准线与![]() 轴的交点,若线段AB的中点C在椭圆上,则该椭圆的离心率为 ( )
轴的交点,若线段AB的中点C在椭圆上,则该椭圆的离心率为 ( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
7、设![]() 为坐标原点,点M坐标为
为坐标原点,点M坐标为![]() ,若点
,若点![]() 满足不等式组:
满足不等式组: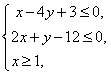 则使
则使![]() 取得最大值的点
取得最大值的点![]() 的个数是( ) .
的个数是( ) .
A.![]() B.
B.![]() C.
C.![]() D.无数个
D.无数个
8、已知函数![]() 的某两个交点横坐标为x1、x2,若
的某两个交点横坐标为x1、x2,若![]() ,则该函数的一个递增区间可以是( )A.
,则该函数的一个递增区间可以是( )A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、已知曲线C:![]() 与函数
与函数![]() 的图像分别交于
的图像分别交于![]() ,则
,则![]() ( )
( )
A.16 B.8 C. 4 D. 2
10.设M是![]() 内一点,且
内一点,且![]() ,
,![]() =30°.定义
=30°.定义![]() ,其中
,其中![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的面积.若
的面积.若![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.18 B.16 D.9 D.8
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在答题卡相应位置上)
11、已知![]() ,则p的值是
,则p的值是
12、已知函数![]() 的导数
的导数![]()
![]() 处取到极大值,则a的取值范围是
处取到极大值,则a的取值范围是
13、一个五位数由数字0,1,1,2,3构成, 这样的五位数的个数为_
14、已知三棱锥S—ABC的各顶点都在一个半径为r的球面上,球心O在AB上,SO⊥底面ABC,AC=![]() r ,则球的体积与三棱锥体积之比是 。
r ,则球的体积与三棱锥体积之比是 。
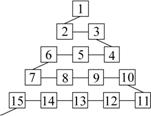 15、如图是从事网络工作者经常用来解释网络运作的蛇形模型:
15、如图是从事网络工作者经常用来解释网络运作的蛇形模型:
数字1出现在第1行;数字2,3出现在第2行;数字6,5,4
(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依
此类推.则第99行从左至右算第67个数字为 .
三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)
16、(本题满分12分)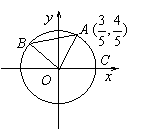 如图
如图![]() 、
、![]() 是单位圆
是单位圆![]() 上的点,
上的点,![]() 是圆与
是圆与![]() 轴正半轴的交点,
轴正半轴的交点,![]() 点的坐标为
点的坐标为![]() ,三角形
,三角形![]() 为正三角形.
为正三角形.
(1)求![]() ;
;
(2)求![]() 的值.
的值.
17、(本题满分12分)一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:
![]()
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数![]() 的分布列和数学期望.
的分布列和数学期望.

18、(本题满分12分)如图,四棱锥![]() 的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=
的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=![]() ,E为PC的中点.
,E为PC的中点.
(1)求直线DE与平面PAC所成角的大小;
(2)在线段PC上是否存在一点M,使PC⊥平面MBD成立.并说明理由。
19、(本题满分12分)
设![]() 是数列
是数列![]() 的前n项和,满足
的前n项和,满足![]() ,数列
,数列![]() 满足
满足![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 的每一项总小于它后面的项,求a的取值范围。
的每一项总小于它后面的项,求a的取值范围。
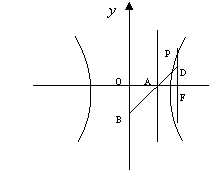
20. (本题满分13分)如图,已知双曲线![]() ,其右准线交x轴于点A, 双曲线虚轴的下端点为B,过双曲线的右焦点F
,其右准线交x轴于点A, 双曲线虚轴的下端点为B,过双曲线的右焦点F![]() 作垂直于x轴的直线交双曲线于点P,若点D满足
作垂直于x轴的直线交双曲线于点P,若点D满足![]()
![]()
 (1)求双曲线的离心率;
(1)求双曲线的离心率;
(2) 若![]() =2,过点B的直线
=2,过点B的直线![]() 交双曲线于M、N两点,问是否存在
交双曲线于M、N两点,问是否存在![]() 轴上的定点C使
轴上的定点C使![]() 为常数,若存在求出C点的坐标,若不存在,请说明理由.
为常数,若存在求出C点的坐标,若不存在,请说明理由.
21、(本题满分14分)已知函数![]()
(1)求证:![]() 为定值
为定值
(2)求:![]() 的值;
的值;
(3)设![]() ,且1<a1<2,
,且1<a1<2,
求证:![]() +…+
+…+![]() <2.
<2.
