苏州中学高三数学综合训练(7)
班级 姓名 得分
一、选择题:
1.在锐角![]() 中,若
中,若![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.(1,
B.(1,![]() )
)
C.![]() D.(―1,1)
D.(―1,1)
2.已知x,y为正实数,且x,a1, a2, y成等差数列,x, b1, b2, y成等比数列,那么![]()
的取值范围是 ( )
A.(0,+∞) B.![]() C.
C.![]() D.[2,4]
D.[2,4]
3.已知函数f (x)(0≤x≤1)
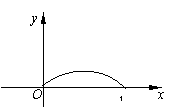 的图象是一段圆弧(如图所示)若
的图象是一段圆弧(如图所示)若![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
C.![]() D.前三个判断都不正确
D.前三个判断都不正确
4.已知![]() 等于 ( )
等于 ( )
A.-![]() B.-
B.-![]() C.
C.![]() D.
D.![]()
5.已知a,b,c为三条不同的直线,且a![]() 平面
平面![]() ,b
,b![]() 平面β,α∩β=c
平面β,α∩β=c
①若a与b是异面直线,则c至少与a,b中的一条相交. ②若a不垂直于c,则a与b一定不垂直. ③若a//b,则必有a//c ④若a⊥b,a⊥c,则必有α⊥β
以上的命题中,正确的是 ( )
A.②③④ B.①③ C.①④ D.②③
6.已知集合A={1,2,3,4,5,6},若a∈A,b∈A,则离心率互不相同的椭圆
![]() 的个数为 ( )
的个数为 ( )
A.15 B.13 C.12 D.11
7.椭圆有如下的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后必过椭圆的另一个焦点.今有一个水平放置的椭圆形台球盘,点A、B是它的两个焦点,其长轴长为2a,焦距为2c(a>c>0),静放在点A的小球(小球的半径不计),从点A沿直线出发,经椭圆壁反弹后第一次回到点A时,小球经过的路程是 ( )
A.2(a-c) B.2(a+c) C.4a D.以上答案均有可能
8.已知函数f(x)=ax(a>0且a≠1),f(a)<1设![]() 则( )
则( )
A.n<s<m B.m<s<n C.s<m<n D.n<m<s
9.区间![]() 所得的象集区间为
所得的象集区间为![]() ,若区间
,若区间![]() 的长度比区间
的长度比区间
![]() 的长度大5,则
的长度大5,则![]() =( )
=( )
A.5 B.10 C.2.5 D.1
10.已知![]() ,
,![]() ,点
,点![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是圆
是圆![]() 上的动点,则
上的动点,则![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:
11.已知x2+xy+y2=3,则x2+y2的范围是 .
12.有一个正四棱锥,它的底面边长与侧棱长均为2,现用一张正方形包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小边长应为 .
13.将函数![]() 的反函数的图象向左平移一个单位,再向下平移一个单位之后,得到函数g(x)的图象,则g(1)+3·g(3)+5·g(5)+7·g(7)+9·g(9)的值等于
..
的反函数的图象向左平移一个单位,再向下平移一个单位之后,得到函数g(x)的图象,则g(1)+3·g(3)+5·g(5)+7·g(7)+9·g(9)的值等于
..
14.已知F1、F2为双曲线![]() =1(a>0,b>0)的焦点,过F2作垂直于x轴的直线,它与双曲线的一个交点为P,且∠PF1F2=30°,则双曲线的渐近线方程为 .
=1(a>0,b>0)的焦点,过F2作垂直于x轴的直线,它与双曲线的一个交点为P,且∠PF1F2=30°,则双曲线的渐近线方程为 .
|
15.如图所示,在排成4×4方阵的16个点中,
中间4个点在某个圆内,其余12个点在圆外.
在16个点中任选3个点构成三角形,其中恰
有两个顶点在圆内的三角形有 个;
至少有一个顶点在圆内的三角形有 个.
16.一只电子蚂蚁在如图2所示的网络线上由原点(0,0)出发,沿向上或向右方向爬至点(m,n)(m,n![]() N),记可能的爬行方法总数为f(m,n), 下列有4逐步形成结论:
N),记可能的爬行方法总数为f(m,n), 下列有4逐步形成结论:
 ①f(2,1)=f(1,2)=3;
①f(2,1)=f(1,2)=3;
②f(2,2)=6;
③f(3,3)=21;
④f(n,n)= ![]()
其中所有正确结论的序号是
三、解答题:
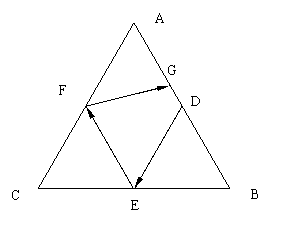 17.一张形状为等边三角形的球桌,设其顶点为
17.一张形状为等边三角形的球桌,设其顶点为![]() .一个球从
.一个球从![]()
边的中点![]() 击出,击中
击出,击中![]() 边上的某点
边上的某点![]() ,并且依次碰击
,并且依次碰击![]() 边于点
边于点
![]() ,最后击中
,最后击中![]() 边于点
边于点![]() ,设
,设![]() ,求
,求![]() 的取值范围.
的取值范围.
(∠DEB=∠CEF,∠EFC=∠AFG)
18.已知集合M是同时满足下列两个性质的函数f(x)的全体:①f(x)在其定义域上是单调增函数或单调减函数;②在f(x)的定义域内存在区间[a,b],使得f(x)在[a,b]上的值域是[a,b].
(1)判断函数y=-x3是否属于集合M?并说明理由.若是,请找出区间[a,b].
(2)若函数y=+t∈M,求实数t的取值范围.
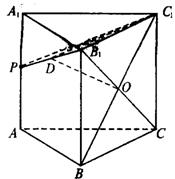
19.如右图,正三棱柱![]() 的所有棱长均为2,
的所有棱长均为2,![]() 是棱
是棱![]() 上的一动点.
上的一动点.
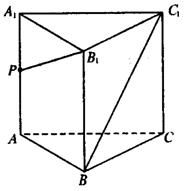 (1)当
(1)当![]() 在棱
在棱![]() 上运动时,
上运动时,![]() 是否有能与平面
是否有能与平面![]() 垂直,说明理由;
垂直,说明理由;
(2)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)在(2)的条件下,求二面角![]() 的大小.
的大小.
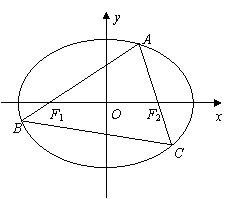
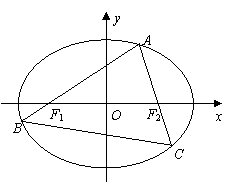 20.如图,
20.如图,![]() 为椭圆
为椭圆![]()
![]() 上的一个动点,弦
上的一个动点,弦![]() 分别过焦点
分别过焦点![]() .当
.当![]() 垂直于
垂直于![]() 轴 时,恰好
轴 时,恰好![]() .
.
(I)求该椭圆的离心率;
(II)设![]() ,
,![]() ,
,
试判断![]() 是否为定值?若是,则求出该定值;若不是,请说明理由.
是否为定值?若是,则求出该定值;若不是,请说明理由.
21. 已知函数![]() 的定义域为[0,1],且同时满足:
的定义域为[0,1],且同时满足:
(1) 对任意![]() ,总有
,总有![]() ;
;
(2) ![]() ;
;
(3) 若![]() ,则有
,则有![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试求![]() 的最大值;
的最大值;
(Ⅲ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]()
求证:![]()
苏州中学数学参考答案及评分标准
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | C | C | B | D | D | A | A | D |
二、填空题
11.[2,6] 12. ![]() 13.15
13.15
14. y=±![]() x
15.60;312
16.①、②、④
x
15.60;312
16.①、②、④
三、解答题
17.解:由![]() 为等边三角形及入射角等于反射角易见
为等边三角形及入射角等于反射角易见![]() ∽
∽![]() ∽
∽![]() ,2分
,2分
∴![]() . 3分
. 3分
不失一般性,设等边![]() 的边长为2,且
的边长为2,且![]() ,
,
则有![]() ,且
,且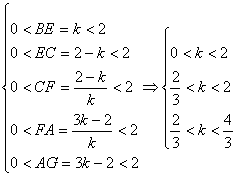
![]() . 8分
. 8分
在![]() 中,由正弦定理得
中,由正弦定理得
![]()
![]() . 10分
. 10分
而![]() , (文12分)
, (文12分)
即![]() . 12分
. 12分
18.解:(1)y=-x3的定义域是R,
y'=-3x2≤0,∴y=-x3在R上是单调减函数.
则y=-x3在[a,b]上的值域是[-b3,-a3].
由 解得:或 (舍去)或 (舍去)
∴函数y=-x3属于集合M,且这个区间是[-,]
(2)设g(x)=+t,则易知g(x)是定义域[1,+∞![]() 上的增函数.
上的增函数.
g(x)∈M,∴存在区间[a,b]![]() [1,+∞
[1,+∞![]() ,满足g(a)=a,g(b)=b.
,满足g(a)=a,g(b)=b.
即方程g(x)=x在[1,+∞![]() 内有两个不等实根.
内有两个不等实根.
[法一]:方程+t=x在[1,+∞![]() 内有两个不等实根,
内有两个不等实根,
等价于方程x-1=(x-t)2在[2t,+∞![]() 内有两个不等实根.
内有两个不等实根.
即方程x2-(4t+4)x+4t2+4=0在[2t,+∞![]() 内有两个不等实根.
内有两个不等实根.
 根据一元二次方程根的分布有
根据一元二次方程根的分布有
解得0<t≤.
因此,实数t的取值范围是0<t≤.
[法二]:要使方程+t=x在[1,+∞![]() 内有两个不等实根,
内有两个不等实根,
即使方程=x-t在[1,+∞![]() 内有两个不等实根.
内有两个不等实根.
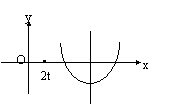
如图,当直线y=x-t经过点(1,0)时,t=,
当直线y=x-t与曲线y=相切时,
方程=x-t两边平方,得x2-(4t+4)x+4t2+4=0,由△=0,得t=0.
因此,利用数形结合得实数t的取值范围是0<t≤.
19. 解:(1)无论![]() 在
在![]() 的任何位置
的任何位置![]() 都不能与平面
都不能与平面![]() 垂直.
垂直.
反证法:假设![]() 平面
平面![]() ,则
,则![]() ,必有
,必有![]() 与
与![]() 重合;
重合;![]() 平面
平面![]() ,则必有
,则必有![]() ,即
,即![]() 与
与![]() 矛盾. 3分
矛盾. 3分
(2)连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,又
,又![]() , 4分
, 4分
∴![]() 平面
平面![]() ,且垂足为
,且垂足为![]() .
.
∴![]() .取
.取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() 面
面![]() 而
而![]() 为
为![]() 在面
在面![]() 内的射影,由三垂线逆定理知
内的射影,由三垂线逆定理知![]() ,而四边形
,而四边形![]() 为正方形, 7分
为正方形, 7分
∴易见![]() 为棱
为棱![]() 的中点.
的中点.
∴![]() . 8分
. 8分
(3)由(2)知,![]() 面
面![]() ,过
,过![]() 作
作![]() 于
于![]() ,连
,连![]() 则
则![]() 所求二面角的平面角, 9分
所求二面角的平面角, 9分
在![]() 中(如右图)
中(如右图)![]() ,
,
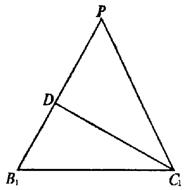
∴
在![]() 中,
中,![]() ,
,
![]() . 11分(文12分)
. 11分(文12分)
∴所求二面角大小是![]() . 12分
. 12分
20. 解:(I)当![]() C垂直于x轴时,
C垂直于x轴时,![]()
 由
由![]() ,得
,得![]() ,
,![]()
在Rt△![]() 中,
中,![]()
![]()
解得 ![]() =
=![]() .
.
(II)由![]() =
=![]() ,则
,则![]() ,
,![]() .
.
焦点坐标为![]() ,则椭圆方程为
,则椭圆方程为![]() ,
,
化简为![]() .设
.设![]() ,
,![]() ,
,
①若直线![]() 的斜率存在,则直线
的斜率存在,则直线![]() 方程为
方程为![]()
代入椭圆方程有![]() .
.
由韦达定理得:![]() ,∴
,∴![]() 所以
所以
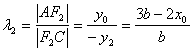 ,同理可得
,同理可得![]()
故![]() =
=![]() .
.
②若直线![]()
![]() 轴,
轴,![]() ,
,![]() ,
,![]()
∴![]() =6.
=6.
综上所述:![]() 是定值6.
是定值6.
