| ………………………………班级……………………姓名……………………考场……………………座位号……………………………… 密 封 线 内 不 要 答 题 ……………………密……………………封……………………装 ……………………订……………………线…………………… |
2006届无为县普通高中高三第二次六校联考
文科数学试题
一、单项选择题(本大题共有12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项符合题目要求.)
1.已知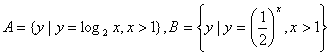 ,则A∩B等于( )
,则A∩B等于( )
A.![]() B.
B. ![]() C.
C.
![]() D.(0,2)
D.(0,2)
2.在以下关于向量的命题中,不正确的命题个数是
①若向量![]() ,向量
,向量![]() ,则
,则![]() ;
;
②四边形![]() 是菱形的充要条件是
是菱形的充要条件是![]() ,且
,且![]() ;
;
③点![]() 是
是![]() 的重心,则
的重心,则![]() .
.
④![]() 中,
中,![]() 和
和![]() 夹角等于
夹角等于![]() .
.
A. 0 B.1 C.2 D.3
3.设命题甲:![]() ,命题乙:
,命题乙: ![]() ,那么: ( )
,那么: ( )
A.甲是乙的充分不必要条件 B.甲是乙的必要不充分条件
C.甲是乙的充要条件 D.甲是乙的不充分不必要条件
4.设![]() 与
与![]() 是两个不共线的向量,且向量
是两个不共线的向量,且向量![]() 与
与![]() 共线,则
共线,则![]() = ( )
= ( )
A.0
B.![]() C.
C.![]() D.
D.![]()
5.已知A是△ABC的一个内角,且![]() ,则△ABC是
( )
,则△ABC是
( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.形状不确定
6.一个公比q为正数的等比数列{a n},若a1+a2=20 ,a3+a4=80 ,则a5+a6等于
A.120 B. 240 C.320 D. 480
7.已知函数![]() ,则
,则![]() 的值是 ( )
的值是 ( )
A.9
B.![]() C.-9
D.
C.-9
D. ![]()
8.函数![]() 的反函数是
的反函数是
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
![]() 9.设数列{an}是等差数列,且a2=-6, a8=6,Sn是数列{an}的前n项和,则
9.设数列{an}是等差数列,且a2=-6, a8=6,Sn是数列{an}的前n项和,则
A.S4<S5 B.S4=S5 C.S6<S5 D.S6=S5
10.已知函数y=f(x)是R上的偶函数,且在(-∞,0![]() 上是减函数,若f(a)≥f(2),则实数a的取值范围是
上是减函数,若f(a)≥f(2),则实数a的取值范围是
A、a≤2 B、 a≤-2或a≥2 C、a≤-2 D、 -2≤a≤2
11、定义在R上的函数f(x)是奇函数,若f(x)的最小正周期是![]() ,且当
,且当![]() 时,f(x)=sinx,则
时,f(x)=sinx,则![]() 的值为
( )
的值为
( )
![]()
![]()
![]()
![]()
12.若不等式![]() 对
对![]() 恒成立,则关于
恒成立,则关于![]() 的不等式
的不等式![]() 的解为 A.
的解为 A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上.)
13.已知![]() 则cos2β=____________.
则cos2β=____________.
14.已知![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,则切点
平行,则切点![]() 的坐标是 ____________.
的坐标是 ____________.
15.已知函数f(x)=log2(x2-4x+3),则此函数的单调递增区间是__________.
16.定义运算![]() 为:
为:![]() ,例如,
,例如,![]() ,则函数
,则函数![]() 的值域为 .
的值域为 .
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知点A(3,0),B(0,3),C![]()
(1)
若![]() ,求
,求![]() 的值;
的值;
(2) 若![]() ,其中
,其中![]() 是原点,且
是原点,且![]() ,求
,求![]() 与
与![]() 的夹角。
的夹角。
 18.(本题满分12分.)
18.(本题满分12分.)
已知![]() .
.
(1) 求sinx -cos x的值.
(2)求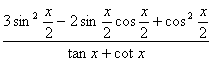 的值.
的值.

19.(本小题满分12分)
已知函数f(x)=abx(a,b为常数)的图象经过点P(1,![]() )和Q(4,8)
)和Q(4,8)
(1) 求函数f(x)的解析式;
(2) 记an=log2 f(n),n是正整数,Sn是数列{an}的前n项和,求![]() 的最小值。
的最小值。
20.(本小题满分12分)
已知函数![]() 1)
1)
(1) 证明:函数![]() 在(
在(![]() 上为增函数。
上为增函数。
(2)
用反证法证明方程![]() 没有负实数根。
没有负实数根。
21.(本小题满分12分)
设二次函数![]() ,已知不论
,已知不论![]() 为何实数,恒有
为何实数,恒有![]()
(1)
求证:![]()
(2)
求证:![]()

22.(本小题满分14分)
设![]() 是函数
是函数![]() 的两个极值点,且
的两个极值点,且![]() .
.
(1) 证明:![]() ;
;
(2) 求实数![]() 的取值范围;
的取值范围;
(3) 若函数![]() ,证明:当
,证明:当![]() 时,
时,![]()
2006届无为县普通高中高三第二次六校联考文科数学试题
参考答案及评分标准
一、单选题:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | B | A | D | B | C | B | D | B | B | C | A |
二、填空题:
13. ![]() 14. (1, 0)_或(-1,-4) 15.
14. (1, 0)_或(-1,-4) 15.![]() 16.
16.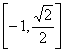
三、解答题:
17.解:(1)![]() ……………2分
……………2分
![]() 得:
得:![]()
![]() 上式平方,解得:
上式平方,解得:![]() ………………6分
………………6分
(2)![]()
![]() ……………9分
……………9分
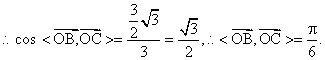 ………12分
………12分
18.解:(1) 法一:由![]() 两边平方得:1+2 sinx cosx=1/25, 2 sinx
cosx=-24/25
两边平方得:1+2 sinx cosx=1/25, 2 sinx
cosx=-24/25
∴ ( sinx –cosx)2=1-2 sinx cosx=49/25; …………………3分
由于![]() ,sinx<0,cosx>0; sinx –cosx<0
,sinx<0,cosx>0; sinx –cosx<0
![]()
…………………6分
法二:联立方程:

(2) ……………12分
……………12分
19.解:(1)因为函数f(x)=abx(a,b为常数)的图象经过点P,Q则有
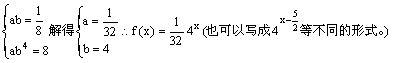 ………5分
………5分
(2)an=log2f(n)=log2![]() =2n-5
=2n-5
因为an+1- an=2(n+1)-5-(2n-5)=2;所以{an}是首项为-3,公差为 2的等差数列(不写此步骤要扣2分)。 ……………8分
所以![]()
![]() 当n=2时,
当n=2时,![]() 取最小值-4 …….12分
取最小值-4 …….12分
20.解:(1)任取![]() 且
且![]() 则
则![]() 又
又![]() 则
则![]()
于是![]() ,而
,而
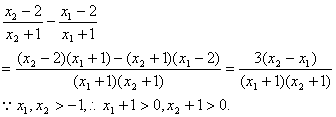
则![]() 于是
于是

故![]() 在
在![]() 上为增函数。
……………6分
上为增函数。
……………6分
(2)
设存在![]() 满足
满足![]() ,则
,则
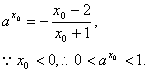 ……………8分
……………8分
解不等式![]() ,得
,得
![]() ,这与假设矛盾,故不存在负实数根。 ……………12分
,这与假设矛盾,故不存在负实数根。 ……………12分
21.解:(1)![]() 且
且![]() 恒成立
恒成立
![]()
![]() 且
且![]() 恒成立
恒成立
![]() ……………3分
……………3分
从而![]() ……………6分
……………6分
(2)![]()
![]() ……………8分
……………8分
![]() 时,
时,![]() 即
即![]() 恒成立,
恒成立,
![]() 即
即![]() 恒成立。
恒成立。
![]() ……………12分
……………12分
22.解:(1)![]() 是
是![]() 的两个极植点,
的两个极植点,![]() 是方程
是方程![]() 的两个实数根.
的两个实数根.
![]()
![]() …………4分
…………4分
(2)设![]()
![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数
上是减函数
![]()
![]() …………………8分
…………………8分
(3)∵X1、X2是方程f′(x)=0的两个实数根,
![]() ,
,
![]()
![]()
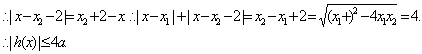 ………..14分
………..14分