盐城市大冈中学2007届
高三数学练习(三)
一.选择题:
1.已知集合M=![]() ,N=
,N=![]() ,那么M
,那么M![]() N=( )
N=( )
A.(0,1) B.(0,1),(1,2) C.{y|y=1或y=2} D.{y|y![]() 1}
1}
2.集合M=![]() ,且
,且![]() .则实数a的取值范围是( )
.则实数a的取值范围是( )
A. a![]() -1 B.
a
-1 B.
a![]() 1 C. a
1 C. a![]() -1 D.a
-1 D.a![]() 1
1
3.函数![]() (x)=
(x)= ![]() 在区间(1,+
在区间(1,+![]() )上是增函数,那么实数a的取值范围是 ( )
)上是增函数,那么实数a的取值范围是 ( )
 |
A.[0,1] B.
4.下列各图中,可表示函数y=![]() (x)的图象的只可能是 ( )
(x)的图象的只可能是 ( )
5.函数![]() (x)=
(x)= ![]() 在区间[1,2]上存在反函数的充分必要条件是( )
在区间[1,2]上存在反函数的充分必要条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.二次函数y=![]() (x)满足
(x)满足![]() (5+x)=
(5+x)= ![]() (5-x),且
(5-x),且![]() (x)=0有两个实数根x1,x2,则x1+x2等于 ( )
(x)=0有两个实数根x1,x2,则x1+x2等于 ( )
A.0 B.5 C.10 D.不能确定
7.函数y=![]() (x)的图象与
(x)的图象与![]() 的图象关于直线y=x对称,则F(x)=
的图象关于直线y=x对称,则F(x)=![]() 的单调递增区间为 ( )
的单调递增区间为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.定义两种运算:![]()
![]() ,则函数
,则函数![]() (x)=
(x)= ![]() 为 ( )
为 ( )
A.奇函数 B.偶函数 C.奇函数且为偶函数 D.非奇且非偶函数
9.已知函数y=![]() (x)在(0,2)上是增函数,函数
(x)在(0,2)上是增函数,函数![]() (x+2)是偶函数,则正确的是( )
(x+2)是偶函数,则正确的是( )
A.![]() (1)<
(1)<![]()
![]() <
< ![]()
![]() B.
B.![]()
![]() <
<![]() (1)<
(1)<![]()
![]()
C.![]()
![]() <
<![]()
![]() <
<![]() (1)
D.
(1)
D.![]()
![]() <
<![]() (1)<
(1)<![]()
![]()
10.命题P:若a.b![]() R,则
R,则![]() >1是
>1是![]() >1的充分而不必要条件:命题q:函数
>1的充分而不必要条件:命题q:函数![]() 的定义域是
的定义域是![]() .则 ( )
.则 ( )
A.“ p或q”为假 B. “p且q”为真 C. p真q假 D. p假q真
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二.填空题:
11.设A={1,2},B={x|x![]() A}若用列举法表示,则集合B是
A}若用列举法表示,则集合B是
12.含有三个实数的集合可表示为![]() ,则
,则![]()
13.关于x的方程![]() 有负根,则a的取值范围是_______________
有负根,则a的取值范围是_______________
14.![]() 在R上为减函数,则
在R上为减函数,则![]() .
.
15.若不等式![]() 和
和![]() >0均不成立,则a的取值范围是
>0均不成立,则a的取值范围是
16.以下命题:①“菱形的两条对角线互相平分”的逆命题;②![]() 或{0}
或{0}![]()
![]() ;③对于命题p且q,若p假q真,则p且q为假;④有两条相等且有一个角是
;③对于命题p且q,若p假q真,则p且q为假;④有两条相等且有一个角是![]() “是”一个三角形为等边三角形的充要条件。其中为真命题的序号为
“是”一个三角形为等边三角形的充要条件。其中为真命题的序号为
三.解答题:
17.已知二次函数![]() (x)满足条件
(x)满足条件![]() (0)=1,及
(0)=1,及![]() (x+1)--
(x+1)--![]() (x)=2x
(x)=2x
(1)求![]() (x)的解析式
(x)的解析式
(2)求![]() (x)在[-1,1]上的最值
(x)在[-1,1]上的最值
18、设a>0且a≠1,![]() (x≥1)
(x≥1)
(Ⅰ)求函数f(x)的反函数f-1(x)及其定义域;
(Ⅱ)若![]() ,求a的取值范围。
,求a的取值范围。
19.已知不等式![]()
⑴若对于所有实数x,不等式恒成立,求m的取值范围
⑵若对于m![]() [-2,2]不等式恒成立,求x的取值范围
[-2,2]不等式恒成立,求x的取值范围
20.设函数![]() (x)是定义在
(x)是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() (x)=
(x)= ![]() (1)求:当
(1)求:当![]() 时
时![]() (x)的表达式。(2)若
(x)的表达式。(2)若![]() (x)在
(x)在![]() 上是增函数,求a的取值范围。(3)是否存在a,使得当
上是增函数,求a的取值范围。(3)是否存在a,使得当![]() 时,
时,![]() (x)有最大值-6.
(x)有最大值-6.
21.已知函数![]() (x)=
(x)=![]() ,设方程
,设方程![]() (x)=x有两个实根
(x)=x有两个实根![]() ,
,![]() ,(1)如果
,(1)如果![]() <2<
<2<![]() <4,设函数
<4,设函数![]() (x)的对称轴为x=
(x)的对称轴为x=![]() ,求证
,求证![]() >-1;(2)如果0<
>-1;(2)如果0<![]() <2,且
<2,且![]() (x)=x的两实根相差为2,求实数b的取值范围。
(x)=x的两实根相差为2,求实数b的取值范围。
参考答案
1~5、DCADD 6~10、CDABD
11、![]() ,12、-1,13、-3<a<1;14、
,12、-1,13、-3<a<1;14、![]() ;15、-2<a≤--1/4;
;15、-2<a≤--1/4;
16、234
17.(1) ![]()
∴a=1且b=-1∴![]()
(2) ∵![]()
∴当![]() 是有最小值
是有最小值![]() ,
,![]() 时有最大值3
时有最大值3
(18) 解 (Ⅰ)![]()
当a>1时,定义域为![]()
当0<a<1时,定义域为![]()
(Ⅱ) ![]()
即![]()
即![]()
即
∴![]()
19.(1)原不等式等价于![]() 对任意实数x恒成立
对任意实数x恒成立
∴![]() ∴
∴![]()
(2)设![]() 要使
要使![]() 在[-2,2]上恒成立,当且仅当
在[-2,2]上恒成立,当且仅当

∴![]()
∴![]() 的取值范围是
的取值范围是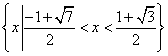
20.(1)当![]() 时,
时,![]() ,此时
,此时![]()
(2) ∵![]() 在
在![]() 上是增函数∴
上是增函数∴![]() 在
在![]() 上恒成立
上恒成立
令![]() ,则
,则![]() 在
在![]() 上是增函数,既
上是增函数,既![]() 从而a>-1
从而a>-1
(3)当a>-1时,由(2)可得![]() ,不合题意,舍去.
,不合题意,舍去.
当![]() 时,令
时,令![]() ,得
,得![]()
若![]() ,则
,则![]() ,既
,既![]()
此时![]()
同理可得,若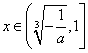 时,
时, ![]()
∴![]() ,既
,既
∴![]() ,故
,故![]() =2,既
=2,既![]() +8
+8
又![]()
故存在a=![]() ,使得
,使得![]() 时,
时,![]() 有最大值-6
有最大值-6
21.(1) ∵![]() 则
则![]()
设![]() ;∵
;∵![]()
∴![]() 既
既![]()
又∵![]() ∴
∴![]()
∴![]()
(2) ![]() ∴
∴![]() 与
与![]() 同号,又∵0<
同号,又∵0<![]() <2
<2
∵![]() ∴
∴![]()
∴![]()
由![]() 既
既![]() 代入上式有
代入上式有![]()
∴![]()