2005年全国高考数学试卷三(四川理)
(必修+选修II)
第一卷(选择题,共60分)
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、 已知![]() 为第三象限的角,则
为第三象限的角,则![]() 所在的象限是( )
所在的象限是( )
A 第一或第二象限 B 第二或第三象限 C第一或第三象限 D 第二或第四象限
2、已知过点![]() 和
和![]() 的直线与直线
的直线与直线![]() 平行,则的值为 ( )
平行,则的值为 ( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3、若![]() 的展开式中
的展开式中![]() 的系数是( )
的系数是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
4、设三棱柱![]() 的体积为
的体积为![]() ,
,![]() 分别是侧棱
分别是侧棱![]() 、
、![]() 上的点,且
上的点,且![]() ,则四棱锥
,则四棱锥![]() 的体积为( )
的体积为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5、![]() ( )
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
6、若![]() ,则( )
,则( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
7、设![]() ,且
,且![]() ,则( )
,则( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
8、![]() ( )
( )
A ![]() B
B ![]() C 1 D
C 1 D ![]()
9、已知双曲线![]() 的焦点为
的焦点为![]() ,点
,点![]() 在双曲线上且
在双曲线上且![]() ,则点
,则点![]() 到
到![]() 轴的距离为( )
轴的距离为( )
A ![]() B
B ![]() C
C ![]() D
D
![]()
10、设椭圆的两个焦点分别为![]() ,过
,过![]() 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点![]() ,若
,若![]() 为等腰直角三角形,则椭圆的离心率为( )
为等腰直角三角形,则椭圆的离心率为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
11、不共面的四个定点到平面![]() 的距离都相等,这样的平面
的距离都相等,这样的平面![]() 共有( )
共有( )
A 3个 B 4个 C 6个 D 7个
12、计算机中常用的十六进制是逢16进1的记数制,采用数字0-9和字母A-F共16个记数符号;这些符号与十进制的数的对应关系如下表:
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六进制表示:E+D=1B,则![]() ( )
( )
A 6E B 72 C 5F D B0
二、填空题:本大题共4 个小题,每小题4分,共16分,把正确答案填在题中横线上。
13、已知复数:![]() ,复数
,复数![]() 满足
满足![]() ,则复数
,则复数![]()
14、已知向量![]() ,
,![]() ,
,![]() ,且A、B、C三点共线,则
,且A、B、C三点共线,则![]()
15、设![]() 为平面上过点
为平面上过点![]() 的直线,
的直线,![]() 的斜率等可能地取
的斜率等可能地取![]() ,用
,用![]() 表示坐标原点到
表示坐标原点到![]() 的距离,则随机变量
的距离,则随机变量![]() 的数学期望
的数学期望![]() 。
。
16、已知在![]() 中,
中,![]() ,
,![]() 是
是![]() 上的点,则点
上的点,则点![]() 到
到![]() 的距离乘积的最大值是
的距离乘积的最大值是
三、解答题:本大题共6个小题,共74分。
17、(本小题满分12分)
设甲、乙、丙三台机器是否需要照顾相互没有影响,已知在某一小时内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照顾的概率为0.125
(Ⅰ)求甲、乙、丙每台机器在这个小时内需要照顾的概率分别为多少;
(Ⅱ)计算这个小时内至少有一台机器需要照顾的概率
18、(本小题满分12分)
 如图,在四棱锥V-ABCD中,底面ABCD是正方形,
如图,在四棱锥V-ABCD中,底面ABCD是正方形,
侧面VAD是正三角形,平面VAD⊥底面ABCD
(Ⅰ)证明AB⊥平面VAD
(Ⅱ)求面VAD与面VDB所成的二面角的大小
19、(本小题满分12分)
![]() 中,内角
中,内角![]() 的对边分别是
的对边分别是![]() ,已知
,已知![]() 成等比数列,且
成等比数列,且![]()
(Ⅰ)求![]() 的值
的值
(Ⅱ)设![]() ,求
,求![]() 的值。
的值。
20(本小题满分12分)
在等差数列![]() 中,公差
中,公差![]() ,
,![]() 是
是![]() 与
与![]() 的等比中项,已知数列
的等比中项,已知数列![]()
![]()
![]() 成等比数列,求数列
成等比数列,求数列![]() 的通项
的通项![]()
21、(本小题满分12分)
设![]() ,
,![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是
是![]() 的垂直平分线。
的垂直平分线。
(Ⅰ)当且仅当![]() 取何值时,直线
取何值时,直线![]() 经过抛物线的焦点
经过抛物线的焦点![]() ?证明你的结论;
?证明你的结论;
(Ⅱ)当直线![]() 的斜率为2时,求
的斜率为2时,求![]() 在
在![]() 轴上截距的取值范围。
轴上截距的取值范围。
22、(本小题满分14分)
已知函数![]() ,
,![]()
(Ⅰ)求![]() 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设![]() ,函数
,函数![]() ,若对于任意
,若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围
的取值范围
2005年全国高考数学试卷三(四川理) 参考答案
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | C | A | C | C | B | C | D | D | A |
二、填空题:本大题共4 个小题,每小题4分,共16分,把正确答案填在题中横线上。
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
三、解答题:本大题共6个小题,共74分。
17.解:(Ⅰ)求已知得![]()
![]()
![]()
解得:![]() ,
,![]() ,
,![]()
所以甲、乙、丙每台机器在这个小时内需要照顾的概率分别为0.2,0.25,0.5
(Ⅱ)记![]() 的对立事件为
的对立事件为![]() ,
,![]() 的对立事件为
的对立事件为![]() ,
,![]() 的对立事件为
的对立事件为![]() ,
,
则:![]() ,
,![]() ,
,![]()
于是![]()
所以这个小时内至少有一台机器需要照顾的概率为0.7
18.方法一:(Ⅰ)证明:
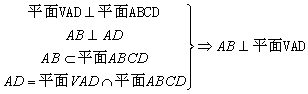
(Ⅱ)解:取VD的中点E,连结AE,BE
∵VAD是正三角形
∴AE⊥VD,AF=![]() AD
AD
∵AB⊥平面VAD ∴AB⊥AE
又由三垂线定理知BE⊥VD
因此,![]() 是所求二面角的平面角
是所求二面角的平面角
于是,![]()
即得所求二面角的大小为![]()
方法二:以D为坐标原点,建立如图所示的坐标系。
(Ⅰ)证明:不妨设![]() ,则
,则![]() ,
,![]()

由![]() ,得
,得![]()
又![]() ,因而
,因而![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() 都垂直。
都垂直。
∴![]() 平面
平面![]()
(Ⅱ)解:设![]() 为
为![]() 中点,则
中点,则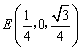
![]()
由![]() ,得
,得![]() ,又
,又![]()
因此,![]() 是所求二面角的平面角。
是所求二面角的平面角。
∵
∴解得所求二面角的大小为![]()
19.解:(Ⅰ)由![]() 得
得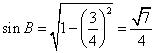
由![]() 及正弦定理得
及正弦定理得![]()
于是![]()
![]()
![]()
![]()
![]()
![]()
![]()
(Ⅱ)由![]() 得
得![]() ,由
,由![]() 可得
可得![]() ,即
,即![]()
由余弦定理 ![]() 得
得![]()
![]()
∴ ![]()
20.解:依题设得![]() ,
,![]()
∴![]() ,整理得
,整理得![]()
∵![]() ∴
∴![]()
得![]()
所以,由已知得![]() 是等比数列
是等比数列
由![]() ,所以数列
,所以数列![]()
![]() 也是等比数列,首项为1,
也是等比数列,首项为1,
公比为![]() ,由此得
,由此得![]()
等比数列![]() 的首项
的首项![]() ,公比
,公比![]() ,所以
,所以![]()
即得到数列![]() 的通项为
的通项为![]()
21.解:(Ⅰ)![]() 两点到抛物线的准线的距离相等,
两点到抛物线的准线的距离相等,
∵抛物线的准线是![]() 轴的平行线,
轴的平行线,![]() ,依题意
,依题意![]() 不同时为0
不同时为0
∴上述条件等价于![]()
∵![]()
∴上述条件等价于![]()
即当且仅当![]() 时,
时,![]() 经过抛物线的焦点
经过抛物线的焦点![]() 。
。
(Ⅱ)设![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,依题意得
,依题意得![]() 的方程为
的方程为![]() ;过点
;过点![]() 的直线方程可写为
的直线方程可写为![]() ,所以
,所以![]() 满足方程
满足方程![]()
得![]()
![]() 为抛物线上不同的两点等价于上述方程的判别式
为抛物线上不同的两点等价于上述方程的判别式![]() ,即
,即![]()
设![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,则
,则
![]() ,
,![]()
由![]() ,得
,得![]() ,于是
,于是![]()
即得![]() 在
在![]() 轴上截距的取值范围为
轴上截距的取值范围为![]()
22.解:对函数![]() 求导,得
求导,得
![]()
![]()
令![]() 解得
解得 ![]() 或
或![]()
当![]() 变化时,
变化时,![]() 、
、![]() 的变化情况如下表:
的变化情况如下表:
| x | 0 |
|
|
|
|
|
|
| 0 |
| ||
|
|
|
|
|
|
|
所以,当![]() 时,
时,![]() 是减函数;当
是减函数;当![]() 时,
时,![]() 是增函数;
是增函数;
当![]() 时,
时,![]() 的值域为
的值域为![]()
(Ⅱ)对函数![]() 求导,得
求导,得
![]()
因此![]() ,当
,当![]() 时,
时, ![]()
因此当![]() 时,
时,![]() 为减函数,从而当
为减函数,从而当![]() 时有
时有
![]()
又![]() ,
,![]() ,即当
,即当![]() 时有
时有
![]()
任给![]() ,
,![]() ,存在
,存在![]() 使得
使得![]() ,则
,则
![]()
即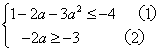
解![]() 式得
式得 ![]() 或
或![]()
解![]() 式得
式得 ![]()
又![]() ,
,
故:![]() 的取值范围为
的取值范围为![]()