2005年普通高等学校招生全国统一考试（天津卷）

数学（文史类）

　　本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试用时120分钟第Ⅰ卷1至2页，第Ⅱ卷3至10页考试结束后，将本试卷和答题卡一并交回

　　祝各位考生考试顺利！

第Ⅰ卷 (选择题 共50分)

　　注意事项：

　　1. 答第Ⅰ卷前，考生务必将自己的姓名、准考号、科目涂写在答题卡上，并在规定位置粘贴考试用条形码

　　2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑如需改动，用橡皮擦干净后，再选涂其他答案标号答在试卷上的无效

　　参考公式：

如果事件A、B互斥，那么　　　　　 　球的体积公式

　　　　　　　　 　　　　　　　　  

如果事件A、B相互独立，那么　　　　  其中R表示球的半径

　　　　　　　　 　　　　　  柱体(棱柱、圆柱)的体积公式

如果事件A在一次试验中发生的概率　　　　　 V_柱体Sh

是P，那么n次独立重复试验中恰好发　　　　其中S表示柱体的底面积，

生k次的概率　　　　　　　　　　　　　　  h表示柱体的高

　　　　　　  

一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中， 只有一项是最符合题目要求的

(1)设集合N}的真子集的个数是(　　)

(A) 16　　　　　　　(B) 8；　　　　　　 (C) 7　　　　　　　 (D) 4

　 (2)已知，则(　　)

(A) 2^b>2^a>2^c；　　　 (B) 2^a>2^b>2^c；　　　 (C) 2^c>2^b>2^a　　　　 (D) 2^c>2^a>2^b

(3)某人射击一次击中的概率为0.6，经过3次射击，此人恰有两次击中目标的概率为(　　)

(A) 　　　　　　(B)　 　　　　　(C)　　 　　　　(D)

(4)将直线2xyl0沿x轴向左平移1个单位，所得直线与圆x²y²2x4y0相切，则实数l的值为

(A) 3或7 　　　　 (B) 2或8　　　　(C) 0或10 　　　　 (D) 1或11

(5)设为平面，为直线，则的一个充分条件是(　　)

(A) 　　　　　　　 (B)

(C) 　　　　　　　　　(D)

(6)设双曲线以椭圆长轴的两个端点为焦点，其准线过椭圆的焦点，则双曲线的渐近线的斜率为(　　)

(A)　　　　　　 (B) 　　　　　　(C)　　　　　　 (D)

(7)给出下列三个命题：①若,则；②若正整数和满足,则；③设为圆上任一点，圆以为圆心且半径为1.当时,圆与圆相切

其中假命题的个数为(　　)

(A) 0　　　　　　　　(B) 1　　　　　　　 (C) 2　　　　　　　 (D)3

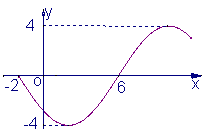(8)函数yA(sinwxj)(w>0，，xÎR)的部分图象如图所示，则函数表达式为 (　　)

(A)

(B)

(C)

(D)

(9)若函数在区间内恒有f(x)>0，则f(x)的单调递增区间为(　　)

(A) 　　　 　　　　　　(B) 　　　

(C) (0,¥) 　　　　　　　　　　(D)

(10)设f(x)是定义在R上以6为周期的函数，f(x)在(0,3)内单调递增，且yf(x)的图象关于直线x3对称，则下面正确的结论是(　　)

(A) f(1.5)<f(3.5)<f(6.5)　　　　　　　　　　(B) f(3.5)<f(1.5)<f(6.5)

(C) f(6.5)<f(3.5)<f(1.5)　　　　　　　　　　(D) f(3.5)<f(6.5)<f(1.5)

第Ⅱ卷 (非选择题 共100分)

　　注意事项：

　　1. 答卷前将密封线内的项目填写清楚

　　2. 用钢笔或圆珠笔直接答在试卷上

二、填空题：本大题共6小题，每小题4分，共24分，把答案填在题中横线上

(11)二项式的展开式中常数项为__________(用数字作答)．

(12)已知，，与的夹角为，以，为邻边作平行四边形，则此平行四边形的两条对角线中较短的一条的长度为__________

(13) 如图，PA⊥平面ABC，∠ACB=90°且PA=AC=BC=a则异面直线PB与AC所成角的正切值等于________．

 (14)在数列{a_n}中，a₁1，a₂2，且N^*)则S₁₀__________

(15)设函数，则函数的定义域为__________

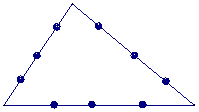
(16)在三角形的每条边上各取三个分点(如图)以这9个分点为顶点可画出若干个三角形若从中任意抽取一个三角形，则其三个顶点分别落在原三角形的三条不同边上的概率为__________(用数字作答)

三、解答题：本大题共6小题，共76分，解答应写出文字说明，证明过程或演算步骤

(17)(本小题满分12分)

已知，，求sina及

(18)(本小题满分12分)

若公比为c的等比数列的首项且满足(n3,4,…)

(Ⅰ)求c的值；

(Ⅱ)求数列的前n项和

（19）（本小题满分12分）

如图，在斜三棱柱中，，侧面与底面ABC所成的二面角为，E、F分别是棱的中点

（Ⅰ）求与底面ABC所成的角

（Ⅱ）证明∥平面

（Ⅲ）求经过四点的球的体积

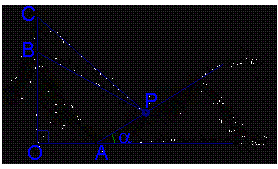(20)(本小题满分12)

某人在一山坡P处观看对面山项上的一座铁塔如图所示，塔及所在的山崖可视为图中的竖线OC，塔高BC80(米)，山高OB=220(米)，OA=200(米)，图中所示的山坡可视为直线l且点P在直线l上，与水平地面的夹角为a，，试问，此人距山崖的水平地面多高时，观看塔的视角ÐBPC最大(不计此人的身高)？

(21)(本小题满分14分)

已知mÎR，设P：和是方程的两个实根，不等式

对任意实数Î[-1,1]恒成立；

Q：函数在(－¥,+¥)上有极值

求使P正确且Q正确的m的取值范围

(22)(本小题满分14分)

抛物线C的方程为，过抛物线C上一点P(x₀,y₀)(x₀¹0)作斜率为k₁,k₂的两条直线分别交抛物线C于A(x₁,y₁)、B(x₂,y₂)两点(P、A、B三点互不相同)，且满足

(Ⅰ)求抛物线C的焦点坐标和准线方程

(Ⅱ)设直线AB上一点M，满足，证明线段PM的中点在y轴上

(Ⅲ)当1时，若点P的坐标为(1,1)，求ÐPAB为钝角时点A的纵坐标的取值范围

2005年高考文科数学天津卷试题及答案

参考答案

一、选择题(每小题5分，共50分)

题号	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
答案	C	A	B	A	D	C	B	A	D	B

二、填空题(每小题4分，共24分)

(11)210；　(12)；　(13)；　(14)35；　(15)(2,1)È(1,2)；　(16)．

三、解答题(共76分，以下各题为累计得分，其他解法请相应给分)

(17)解法一：由题设条件，应用两角差的正弦公式得

，即　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　①

由题设条件，应用二倍角余弦公式得

故　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　②

由①和②式得，

因此，，由两角和的正切公式

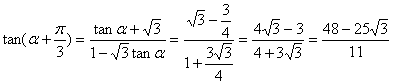
解法二：由题设条件，应用二倍角余弦公式得，

解得　　，即

由可得

由于，且，故a在第二象限于是，

从而

以下同解法一

(18)解：(Ⅰ)解：由题设，当时，，

，

由题设条件可得，因此，即

解得c＝1或

(Ⅱ)解：由(Ⅰ)，需要分两种情况讨论，

当c＝1时，数列是一个常数列，即 (nÎN^*)

这时，数列的前n项和

当时，数列是一个公比为的等比数列，即 (nÎN^*)

这时，数列的前n项和

　　　　　　　　　　　①

①　　 式两边同乘，得

　　　　　 ②

①式减去②式，得

所以(nÎN^*)

（19）解：（Ⅰ）过作平面，垂足为．

连结，并延长交于，

于是为与底面所成的角．

∵，∴为的平分线．

又∵，∴，且为的中点．

因此，由三垂线定理．

∵，且，∴．

于是为二面角的平面角，

即．

由于四边形为平行四边形，得．

（Ⅱ）证明：设与的交点为，则点为的中点．连结．

在平行四边形中，因为的中点，故．

而平面，平面，所以平面．

（Ⅲ）连结．在和中，由于，，，则

≌，故．由已知得．

又∵平面，∴为的外心．

设所求球的球心为，则，且球心与中点的连线．

在中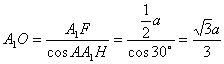，．故所求球的半径，球的体积．

(20)解：如图所示，建立平面直角坐标系，则，，．

直线的方程为，即．

设点的坐标为，则()

由经过两点的直线的斜率公式

，

．

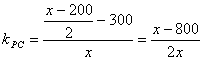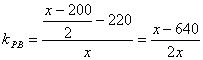由直线到直线的角的公式得

()

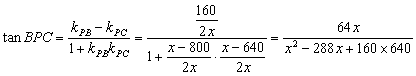
要使达到最大，只须达到最小．

由均值不等式．当且仅当时上式取等号．故当时最大．这时，点的纵坐标为．

由此实际问题知，，所以最大时，最大．故当此人距水平地面60米高时，观看铁塔的视角最大．

 (21)解：(Ⅰ)由题设和是方程的两个实根，得

+＝且＝－2，

所以，

当Î[-1,1]时，的最大值为9，即£3

由题意，不等式对任意实数Î[-1,1]恒成立的m的解集等于不等式的解集由此不等式得

　　　　　①

或　　　　　　　　②

不等式①的解为

不等式②的解为或

因为，对或或时，P是正确的

(Ⅱ)对函数求导

令，即此一元二次不等式的判别式

若D＝0，则有两个相等的实根，且的符号如下：

	(－¥,)		(,+¥)
	+	0	+

因为，f()不是函数f()的极值

若D>0，则有两个不相等的实根和 (<)，且的符号如下：

x	(－¥,)		(，)		(,+¥)
	+	0	－	0	+

因此，函数f()在＝处取得极大值，在＝处取得极小值

综上所述，当且仅当D>0时，函数f()在(－¥,+¥)上有极值

由得或，

因为，当或时，Q是正确得

综上，使P正确且Q正确时，实数m的取值范围为(-¥,1)È

(22)解：(Ⅰ)由抛物线的方程()得，

焦点坐标为，准线方程为．

(Ⅱ)证明：设直线的方程为，

直线的方程为．

①②

点和点的坐标是方程组

的解．将②式代入①式得，

于是，故　③

④⑤

又点和点的坐标是方程组

的解．将⑤式代入④式得．

于是，故．

由已知得，，则．　　⑥

设点的坐标为，由，则．

将③式和⑥式代入上式得，即．

所以线段的中点在轴上．

(Ⅲ)因为点在抛物线上，所以，抛物线方程为．

由③式知，代入得．

将代入⑥式得，代入得．

因此，直线、分别与抛物线的交点、的坐标为

，．

于是，，

．

因为钝角且、、三点互不相同，故必有．

求得的取值范围是或．

又点的纵坐标满足，故

当时，；当时，．

即