2006届数学模拟试卷（文史类）

第1卷（选择题 共60分）

一、  选择题：本大题共12小题，每小题5分，共60分

1.若全集U=R,集合M＝，N＝，则=(　 )

  A.　 B. 　 C. 　　 D.  

2.若则（　 ）

A.　　  B.　　  C.　　  D.

3.条件p：“直线在轴上的截距是在轴上的截距的两倍” ；条件q：“直线的斜率为－2” ，则p是q的（　 ）

A.充分不必要条件　 B.必要不充分条件　C.充要条件　D.非充分也非必要

4.如果的展开式中只有第4项的二项式系数最大，那么展开式中的所有项的系数和是（　 ）

A.0　　　  B.256　　　 C.64　　　 D.

5.为基底向量，已知向量，若A,B,D三点共线，则k的值为（　 ）

A.2　　 B.－3　　　C.－2　　　D.3

6.一个单位有职工160人，其中有业务员120人，管理人员24人，后勤服务人员16人.为了了解职工的身体健康状况，要从中抽取一定容量的样本.现用分层抽样的方法得到业务人员的人数为15人，那么这个样本容量为（　 ）

A.19　　 B.20　　C.21　　　D.22

7.直线与曲线相切于点A（1，3），则b的值为（　 ）

A.3　　  B.－3　　　C.5　　　D.－5

8.在一个的二面角的一平面内有一条直线与二面角的棱成角，则此直线与二面角的另一个面所成的角为（　 ）

A.　　  B.　　 C.　　 D.

9.只用1，2，3三个数字组成一个四位数，规定这三个数必须同时使用，且同一数字不能相邻出现，这样的四位数有（　 ）t

A.6个 　　B.9个　　C.18个　　　D.36个

10.若椭圆的左右焦点分别为，线段被的焦点分成5׃3的两段，则此椭圆的离心率为（　 ）

A.　　 B. 　　　C. 　　 D.

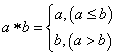11.对任意两实数，定义运算“”如下：，则函数的值域为（　 ）x

A.　　B.　　C.　　D.

12.一种专门占据内存的计算机病毒，开机时占据内存2KB，然后每3分钟自身复制一次，复制后所占据内存是原来的2倍，那么开机后，该病毒占据64MB（1MB＝KB）内存需经过的时间为（　 ）

A.15分钟　　　 B.30分钟　　　 C.45分钟　　　 D.60分钟

第II卷（非选择题 共90分）

二、  填空题：本大题共4小题，每小题4分，共16分.

13.若指数函数的部分对应值如下表：

x	0	2
	1	1.44

则不等式的解集为　　　　　   .

14.数列满足＝　　　　　  .

15.已知实数x,y满足约束条件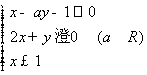，目标函数只有当时取得最大值，则的取值范围是　　　　　  .

16．请阅读下列命题：

　　　 ①直线与椭圆总有两个交点；

　　　 ②函数的图象可由函数按向量平移得到；

　　　 ③函数一定是偶函数；

　　　 ④抛物线的焦点坐标是．

　　回答以上四个命题中，真命题是_______________(写出所有真命题的编号).

三、解答题（共6小题，17—21题每题12分，第22题14分，共74分）

　　　 17．已知向量

　　（I）若，求的值；

　　 (II) 若求函数的值域．

18．在一次历史与地理两门功课的联合考试中,备有6道历史题,4道地理题,共10道题目可供选择,要求学生从中任意选取5道作答,答对4道或5道即为良好成绩．

（I）设对每道题目的选取是随机的，求所选的5道题中至少选取2道地理题的概率；

(II) 若学生甲随机选定了5道题目，且答对任意一道题的概率均为0.6，求甲没有取

　　　　得良好成绩的概率（精确到小数点后两位）．

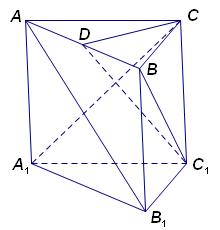19．已知：如图，直三棱柱中，，的中点，

（I）求证：；

(II) 求证：平面；

（III）求异面直线与所成角的余弦值．

20．设是函数的两个极值点，且．

　　　 （I）求证：；

　　　  (II) 求证：．

21．已知数列的前项和为，且＝，数列中，，

点在直线上．

（I）求数列的通项和；

(II) 记，求满足的最大正整数．

22．一条斜率为１的直线与离心率为的双曲线Ｅ：交于　　　 两点，直线与轴交于，且，求直线与双曲线

　　Ｅ的方程．

高三联考数学（文科）参考答案

一、  选择题：（每小题5分，共60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	C	B	D	A	B	A	A	C	D	A	C

二、  填空题：（每小题4分，共16分）

13.（0，1）;　　 14.-2;　　　15.a>0;　　 16.①④.

14.提示：归纳法得到是周期为4的数列，

15.提示：直线过定点（1，0），画出区域后，让直线绕（1，0）旋转得到不等式所表示的平面区域，平移直线观察图象可知，必须满足直线的斜率才符号题意.故a的范围是　　　　　　　　　　　　　 t

三、  解答题:17.解：（I）

(II)

　　　　

　　　　　　　　　　　　　　　　　　　　　 x

故函数的值域为

18.解: （I）法一：所选的5道题中至少有2道地理题的概率为

 

法二：所选的5道题中至少有2道地理题的概率为

　

(II)甲答对4道题的概率为：

甲答对5道题的概率为：

故甲没有获得良好成绩的概率为：

　　　　　　　　　　　　　　　 

19.方法一：（I）证明：

四边形为正方形，连,则

由三垂线定理，得　　　　　　　　　　　　　　　　　　　

（II）证明：连

在△中，由中位线定理得.

又

（III）解：取

令

在直角△

在△

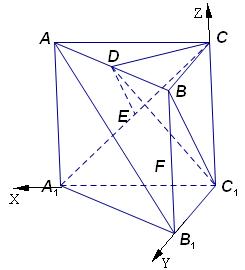
方法二：如图建立坐标系.设则

（I）证：

（II）证：取则

有

又

（III）

20.（I）证明：

（II）证明：设

21.解（1）

.

（II）

因此：

即：

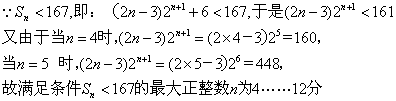
22.解:由①

设直线的方程为，代入①，得：，

即：

②

代入

代入②得