![]()
 2002年广州市高中数学青年教师解题比赛试卷
2002年广州市高中数学青年教师解题比赛试卷
第I卷(选择题共60分)
参考公式:
三角函数和差化积公式 正棱台、圆台的侧面积公式
![]()
![]() 其中
其中![]() 、
、![]() 分别表示
分别表示
![]() 上、下底面周长,l表示斜高或母线长
上、下底面周长,l表示斜高或母线长
![]() 台体的体积公式:
台体的体积公式:![]()
![]() 其中
其中![]() 、
、![]() 分别表示上、下底面积,h表示高
分别表示上、下底面积,h表示高
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.每小题选出答案后,请填下表中.
(1)常数T满足![]() 和
和![]() ,则T的一个值是( ).
,则T的一个值是( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2)在等差数列![]() 中,
中,![]() ,则
,则![]() 的值为( ).
的值为( ).
(A)24 (B)22 (C)20 (D)![]()
(3)设点P对应复数是![]() ,以原点为极点,实轴的正半轴为极轴,建立极坐
,以原点为极点,实轴的正半轴为极轴,建立极坐
标系,则点P的极坐标为( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4)设A、B是两个非空集合,若规定:![]() ,则
,则![]() 等于( )
等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(5)函数![]() 的图象与直线
的图象与直线![]() 的交点个数为( ).
的交点个数为( ).
(A)0 (B)1 (C)2 (D)0或1
(6)设函数![]() (其中
(其中![]() ),则
),则![]() 是
是![]() 为
为
奇函数的( ).
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
 (7)如图,在斜三棱柱
(7)如图,在斜三棱柱![]() 中,∠BAC=90°,
中,∠BAC=90°,![]() ,过
,过![]() 作
作
![]() 底面ABC,垂足为
底面ABC,垂足为![]() ,则( ).
,则( ).
(A)![]() 在直线AC上 (B)
在直线AC上 (B)![]() 在直线AB上
在直线AB上
(C)![]() 在直线BC上 (D)
在直线BC上 (D)![]() 在△ABC内
在△ABC内
(8)电讯资费调整后,市话费标准为:通话时间不超过3分钟收费0.2元;超
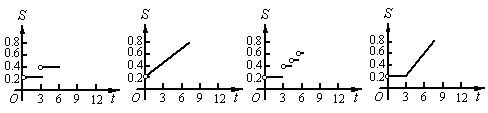 过3分钟,以后每增加1分钟收费0.1元,不足1分钟以1分钟收费.则通话收S(元)与通话时间t(分钟)的函数图象可表示为( ).
过3分钟,以后每增加1分钟收费0.1元,不足1分钟以1分钟收费.则通话收S(元)与通话时间t(分钟)的函数图象可表示为( ).
(A) (B) (C) (D)
(9)以椭圆![]() 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线![]() 的渐近线相
的渐近线相
切的圆的方程为( ).
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(10)已知![]() 的展开式中所有项系数之和为729,则这个展开式中含
的展开式中所有项系数之和为729,则这个展开式中含![]() 项
项
的系数是( ).
(A)56 (B)80 (C)160 (D)180
(11)AB是过圆锥曲线焦点F的弦,l是与点F对应的准线,则以弦AB为直
径的圆与直线l的位置关系( ).
(A)相切 (B)相交 (C)相离 (D)由离心率e决定
(12)定义在R上的函数![]() 的反函数为
的反函数为![]() ,则
,则![]() 是( ).
是( ).
(A)奇函数 (B)偶函数 ( C)非奇非偶函数 (D)满足题设的函数![]() 不存在
不存在
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中的横
线上.
(13)函数![]() 的反函数是
.
的反函数是
.
(14)已知抛物线的焦点坐标为![]() ,准线方程为
,准线方程为![]() ,则其顶点坐标为
,则其顶点坐标为
 .
.
(15)如图,在棱长都相等的四面体A—BCD中,
E、F分别为棱AD、BC的中点,则直线
AF、CE所成角的余弦值为 .
(16)甲、乙、丙、丁、戊共5人参加某项技术比赛,决出了第1名到第5名
的名次. 甲、乙两名参赛者去询问成绩,回答者对甲说:“很遗憾,你
和乙都没拿冠军”,对乙说:“你当然不是最差的.”请从这个回答分析,
5人的名次排列共可能有 种不同情况(用数字作答).
![]()
(17)(本小题满分10分)
已知复数![]() ,其中A、C为△ABC的内角,且三个内角
,其中A、C为△ABC的内角,且三个内角
满足2B=A﹢C.试求![]() 的取值范围.
的取值范围.
18)(本小题满分12分)
已知曲线C上的任一点M![]() (其中
(其中![]() ),到点
),到点![]() 的距离减去它到
的距离减去它到
y轴的距离的差是2,过点A的一条直线与曲线C交于P、Q两点,通过点P和坐标原点的直线交直线![]() 于N.
于N.
(I)求曲线C的方程;
(II)求证:NQ平行于x轴.
(19)(本小题满分12分)
是否存在一个等差数列![]() ,使对任意的自然数n,都有
,使对任意的自然数n,都有![]() …
…![]() .
.
 (20)(本小题满分12分)
(20)(本小题满分12分)
如图,△ABC是一个遮阳棚,点A、B是地面上
南北方向的两定点,正西方向射出的太阳(用点
O表示)光线OCD与地面成锐角![]() .
.
(I)遮阳棚与地面成多少度的二面角时,
才能使遮影△ABD面积最大?
(II)当AC=3,BC=4,AB=5,![]() =30°时,试求出遮影△ABD的最
=30°时,试求出遮影△ABD的最
大面积.
![]()
 (21)(本小题满分14分)
(21)(本小题满分14分)
甲、乙、丙三种食物维生素A、B含量及成本如下表:
| 项 目 | 甲 | 乙 | 丙 |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
某食物营养研究所想用x千克甲种食物、y千克乙种食物、z千克丙种食物
配成100千克混合物,并使混合物至少含有56000单位维生素A和63000
单位维生素B.试用x、y表示混合物的成本M(元);并确定x、y、z的值,
使成本最低.
(22)(本小题满分14分)
定义在![]() 上的函数
上的函数![]() 满足:①对任意
满足:①对任意![]() 、
、![]() ,都有
,都有![]()
![]() ;②当
;②当![]() 时,有
时,有![]() .
.
证明:(I)函数![]() 在
在![]() 上的图象关于原点对称;
上的图象关于原点对称;
(II)函数![]() 在
在![]() 上是单调减函数;
上是单调减函数;
(III)![]() .
.![]()