2006届湖北省黄冈市黄州区统一调研试题
数 学(理科A卷)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试用时120分钟.
第Ⅰ卷(选择题 共60分)
参 考 公 式:
sinαcosβ=![]() [sin(α+β)+sin(α-β)]
[sin(α+β)+sin(α-β)]
cosαsinβ=![]() [sin(α+β)-sin(α-β)]
[sin(α+β)-sin(α-β)]
cosαcosβ=![]() [cos(α+β)+cos(α-β)]
[cos(α+β)+cos(α-β)]
sinαsinβ=-![]() [cos(α+β)-cos(α-β)]
[cos(α+β)-cos(α-β)]
sinα+sinβ=2sin![]()
sinα-sinβ=2cos![]()
cosα+cosβ=2cos![]()
cosα-cosβ=-2sin![]()
S台侧=![]() (c′+c)l(c、c′分别表示上、下底面周长,l表示斜高或母线长)
(c′+c)l(c、c′分别表示上、下底面周长,l表示斜高或母线长)
V台体=![]() (S′+
(S′+![]() +S)h(S′、S分别表示上、下底面积,h表示高)
+S)h(S′、S分别表示上、下底面积,h表示高)
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中恰好发生k次的概率Pn(k)=![]()
一、选择题(本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 已知二次函数f(x)=(x-a)(x-b)-2(a<b),并且α、β(α<β)是方程f(x)=0的两根,则a、b、α、β的大小关系是
A.α<a<b<β B.a<α<β<b
C.a<α<b<β D.α<a<β<b
2.已知θ∈[0,π],f(θ)=sin(cosθ)的最大值为a,最小值为b,g(θ)=cos(sinθ)的最大值为c,最小值为d,则a、b、c、d从小到大的顺序为
A.b<d<a<c B.d<b<c<a
C.b<d<c<a D.d<b<a<c
3.设复数z1=2-i,已知z2=z1,且arg![]() ,则复数z2的值为
,则复数z2的值为
A.1+2i B.1-2i
C.-1+2i D.-1-2i
4. 某地区高中分三类,A类校共有学生4000人,B类校共有学生2000人,C类校共有学生3000人.现欲抽样分析某次考试的情况,若抽取900份试卷进行分析,则从A类校抽取的试卷份数应为
A.450 B.400
C.300 D.200
5.给定两个向量a=(3,4),b=(2,1),若(a+xb)⊥(a-b),则x的值等于
A.-3 B.![]()
C.3
D.-![]()
6. 已知F1、F2为双曲线![]() =1(a>0,b>0)的焦点,过F2作垂直于x轴的直线,它与双曲线的一个交点为P,且∠PF1F2=30°,则双曲线的渐近线方程为
=1(a>0,b>0)的焦点,过F2作垂直于x轴的直线,它与双曲线的一个交点为P,且∠PF1F2=30°,则双曲线的渐近线方程为
A.y=±![]() x B.y=±
x B.y=±![]() x
x
C.y=±![]() x
D.y=±
x
D.y=±![]() x
x
7. 点P在曲线y=x3-x+7上移动,过P点的切线的倾斜角取值范围是
A.[0,π)
B.(0,![]() )∪[
)∪[![]() ,π
,π![]()
C.[0, ![]()
![]() ∪(
∪(![]() ,
,![]()
![]()
D.[0, ![]()
![]() ∪[
∪[![]() ,π)
,π)
8. 若某等差数列{an}中,a2+a6+a16为一个确定的常数,其前n项和为Sn,则以下也为确定的常数的是
A.S17 B.S15
C.S8 D.S7
9.将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次,使点(2,0)与点(-2,4)重合,若点(7,3)与点(m,n)重合,则m+n的值为
A.4 B.-4
C.10 D.-10
10.设方程2-x=lgx的两根为x1、x2,则
A.x1x2<0 B.x1x2=1
C.x1x2>1 D.0<x1x2<1
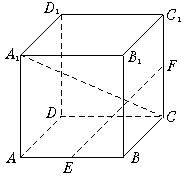
11. 如上图,正方体ABCD—A1B1C1D1 中,E、F分别是AB、CC1的中点,则异面直线A1C与EF所成角的余弦值为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.设数集M={xm≤x≤m+![]() },N={xn-
},N={xn-![]() ≤x≤n},且M、N都是集合{x0≤x≤1}的子集,如果把b-a叫做集合{xa≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值是
≤x≤n},且M、N都是集合{x0≤x≤1}的子集,如果把b-a叫做集合{xa≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4小题;每小题4分,共16分.把答案填在题中的横线上)
13.不等式x2-(a+1)x+a>0的解集为{xx<-1或x>1,x∈R![]() ,则a的取值范围为 .
,则a的取值范围为 .
14.已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为 .
15.某地一种出租车的车费的计算规定如下:基本车费为7元,行程不足3公里时,只收取基本车费;行程不足5公里时,大于等于3公里的那部分,每增加0.5公里,加收车费0.7元,不足0.5公里按0.5公里计算(如:行程为x公里,在4≤x<4.5时,车费为7+0.7×3=9.1元![]() ;行程大于等于5公里时,大于等于5公里的那部分,每增加0.2公里,加收车费0.4元.如果某人从A地到B地,共付车费11元,那么从A地到B地的行程x的范围是 .
;行程大于等于5公里时,大于等于5公里的那部分,每增加0.2公里,加收车费0.4元.如果某人从A地到B地,共付车费11元,那么从A地到B地的行程x的范围是 .

16. 如图所示,在A、B间有四个焊接点,若焊接点脱落,则可能导致电路不通. 今发现A、B之间线路不通,则焊接点脱落的不同情况有 种.
三、解答题(本大题共6小题;共74分.解答过程应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知函数f(x)=a+bsin2x+ccos2x的图象经过点A(0,1),B(![]()
![]() , 1),且当x∈[0,
, 1),且当x∈[0, ![]() ]时,f(x)取得最大值2
]时,f(x)取得最大值2![]() -1.
-1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)是否存在向量m,使得将f(x)的图象按向量m平移后可以得到一个奇函数的图象?若存在,求出满足条件的一个m;若不存在,说明理由.
18.(本小题满分12分)
在袋里装30个小球,其中彩球有:n个红色、5个蓝色、10个黄色,其余为白球.
求:(Ⅰ)如果已经从中取定了5个黄球和3个蓝球,并将它们编上了不同的号码后排成一排,那么使蓝色小球互不相邻的排法有多少种?
(Ⅱ)如果从袋里取出3个都是相同颜色彩球(无白色)的概率是![]() ,且n≥2,计算红球有几个?
,且n≥2,计算红球有几个?
(Ⅲ)根据(Ⅱ)的结论,计算从袋中任取3个小球至少有一个是红球的概率.
19.(本小题满分12分)
设数列{an}满足下列关系式:a1=2a(a≠0,a是常数),an=2a-![]() ;数列{bn}满足关系式bn=
;数列{bn}满足关系式bn=![]() .
.
(Ⅰ)用数学归纳法证明:an≠a;
(Ⅱ)证明数列{bn}是等差数列;
(Ⅲ)求![]() an.
an.
20.(本小题满分12分)
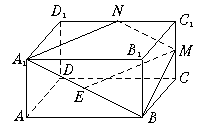
如图,在正四棱柱ABCD—A1B1C1D1中,AA1=![]() AB,点E、M分别为A1B、C1C的中点,过点A1、B、M三点的平面A1BMN交C1D1于点N.
AB,点E、M分别为A1B、C1C的中点,过点A1、B、M三点的平面A1BMN交C1D1于点N.
(Ⅰ)求证:EM∥平面A1B1C1D1;
(Ⅱ)求二面角B—A1N—B1的正切值.
21. (本小题满分12分)
已知函数f(x)=ln(2-x)+ax在(0,1)上是增函数.
(Ⅰ)求实数a的取值范围;
(Ⅱ)若数列{an}满足a1=c∈(0,1)且an+1=ln(2-an)+an(n∈N*),证明0<an<an+1<1;
(Ⅲ)已知![]() an存在,求其值.
an存在,求其值.
22.(本小题满分14分)
已知抛物线y2=2(x+![]() )的焦点为F,准线为l,试判断:是否存在同时满足以下两个条件的双曲线C:
)的焦点为F,准线为l,试判断:是否存在同时满足以下两个条件的双曲线C:
(1)双曲线C的一个焦点是F,相应F的准线为l;
(2)直线m垂直于x-y=0,双曲线C截直线m所得的线段的长为2![]() ,并且截得线段的中点恰好在直线x-y=0上.
,并且截得线段的中点恰好在直线x-y=0上.
若存在,求出这条双曲线的方程;若不存在,说明理由.
参考答案
一、选择题
1.A (根据二次函数的图象即得)
2.A (由正余弦函数的值域和单调性得)
3.D (根据复数乘除法的几何意义)
4.B 5.A
6.D
(由a2+b2=c2及直角三角形PF1F2中的边角关系求得![]() )
)
7.D (过P点的切线的倾斜角正切值的范围即是y=3x2-1的值域[-1,+∞),由此得答案)
8.B (a2+a6+a16=3a1+21d=3a8是一个确定的常数,因此S15=15a8是常数)
9. C ( 提示:点(7,3)与点(m,n)关于点(2,0)与点(-2,4)的中垂线对称)
10.D
(设两根为x1<x2,结合图象知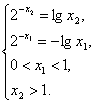 前两个式子相减整理得
前两个式子相减整理得
lg(x1x2)=![]() <0,由此易得答案=
<0,由此易得答案=
11.B (设异面直线A1C与EF所成角为θ,正方体棱长为1,![]() 得
得![]() =1,所以选B)
=1,所以选B)
12.C
(集合M的长度为![]() 、集合N的长度为
、集合N的长度为![]() ,因M、N都是集合{x0≤x≤1}的子集,而{x0≤x≤1}的长度为1,由此得集合M∩N的“长度”的最小值是(
,因M、N都是集合{x0≤x≤1}的子集,而{x0≤x≤1}的长度为1,由此得集合M∩N的“长度”的最小值是(![]() )
)
二、填空题
13.a≤0 14.-37 15.5.4≤x<5.6 16.13
三、解答题
17.
解: (Ⅰ)由题意知![]()
∴b=c=1-a,
∴f(x)=a+![]() (1-a)sin(2x+
(1-a)sin(2x+![]() ). 3分
). 3分
∵x∈[0, ![]() ],
],
∴2x+![]() ∈[
∈[![]() ,
,![]() ].
].
当1-a>0时,
由a+![]() (1-a)=2
(1-a)=2![]() -1,
-1,
解得a=-1;
当1-a<0时,
a+![]() (1-a)·
(1-a)·![]() =2
=2![]() -1,无解;
-1,无解;
当1-a=0时,a=2![]() -1,相矛盾.
-1,相矛盾.
综上可知a=-1.
∴f(x)=-1+2![]() sin(2x+
sin(2x+![]() ). 8分
). 8分
(Ⅱ)∵g(x)=2![]() sin2x是奇函数,将g(x)的图象向左平移
sin2x是奇函数,将g(x)的图象向左平移![]() 个单位,再向下平移一个单位就可以得到f(x)的图象.
10分
个单位,再向下平移一个单位就可以得到f(x)的图象.
10分
因此,将f(x)的图象向右平移![]() 个单位,再向上平移一个单位就可以得到奇函数g(x)=2
个单位,再向上平移一个单位就可以得到奇函数g(x)=2![]() sin2x的图象.
sin2x的图象.
故m=(![]() ,1)是满足条件的一个向量.
12分.
,1)是满足条件的一个向量.
12分.
18.解:(Ⅰ)将5个黄球排成一排只有![]() 种排法,将3个蓝球放在5个黄球所形成的6个空上,有
种排法,将3个蓝球放在5个黄球所形成的6个空上,有![]() 种放法 ,
种放法 ,
∴所求的排法为![]() =5×4×3×2×6×5×4=14400(种).
4分
=5×4×3×2×6×5×4=14400(种).
4分
(Ⅱ)取3个球的种数为![]() =4060,设“3个球全红色”为事件A,“3个球全蓝色”为事件B,“3个球全黄色”为事件C.
=4060,设“3个球全红色”为事件A,“3个球全蓝色”为事件B,“3个球全黄色”为事件C.
P(B)=![]() ,
,
∵A、B、C为互斥事件,
∴P(A+B+C)= P(A)+P(B)+P(C),
即![]()
![]() 取3个球红球的个数n≤2.
取3个球红球的个数n≤2.
又∵n≥2,故n = 2 . 8分
(Ⅲ)记“3个球中至少有一个是红球”为事件D,则![]() 为“3个球中没有红球”,
为“3个球中没有红球”,
P(D)=1-P(![]() )=1-
)=1-![]() 或P(D)=
或P(D)=![]() 12分
12分
19.(Ⅰ) 证明:当n=1时,由a1=2a得a1-a=2a-a=a≠0,∴a1≠a.
即n=1时,结论成立. 1分
设n=k时结论成立,即ak≠a,
则当n=k+1时,
ak+1-a=(2a-![]() )-a
)-a
=a-![]() =
=![]() ≠0.
≠0.
∴ak+1≠a.即n=k+1时,结论成立. 3分
因此,对所有自然数n,都有an≠a. 4分
(Ⅱ)证明: ∵an-a=(2a-![]() )-a
)-a
=![]() ,
,
∴bn=![]()
即bn=![]() .
.
∴bn-bn-1=![]() 是一个常数,即数列{bn}是等差数列.
8分
是一个常数,即数列{bn}是等差数列.
8分
(Ⅲ) 解:∵{bn}是等差数列,其通项为:
bn=b1+(n-1)·![]()
=![]() +(n-1)·
+(n-1)·![]()
=![]() +(n-1)·
+(n-1)·![]() =
=![]() ,
,
又an-a=![]() =
=![]() ,
,
∴an=a+![]() ,
,
∴![]() an=a.
12分
an=a.
12分
20.(法一)(Ⅰ) 证明: 取A1B1的中点F,连EF、C1F.
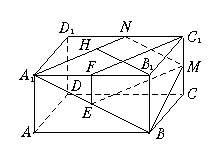
∵E为A1B中点,
∴EF ![]()
![]() BB1.
2分
BB1.
2分
又∵M为CC1中点,
∴EF![]() C1M,
C1M,
∴四边形EFC1M为平行四边形,
∴EM∥FC1. 4分
而EM![]() 平面A1B1C1D1,FC1
平面A1B1C1D1,FC1![]() 平面A1B1C1D1.
平面A1B1C1D1.
∴EM∥平面A1B1C1D1. 6分
(Ⅱ)解: 由(Ⅰ)EM∥平面A1B1C1D1,EM![]() 平面A1BMN,
平面A1BMN,
平面A1BMN∩平面A1B1C1D1=A1N,
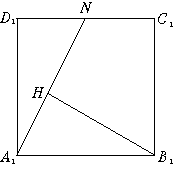
∴A1N∥EM∥FC1,
∴N为C1D1中点.
过B1作B1H⊥A1N于H,连BH,根据三垂线定理BH⊥A1N,
∠BHB1即为二面角B—A1N—B1的平面角. 8分
设AA1=a,则AB=2a.
∵A1B1C1D1为正方形,
∴A1N=![]() a.
a.
又∵△A1B1H∽△NA1D1,
∴B1H=![]() .
.
在Rt△BB1H中,
tanBHB1=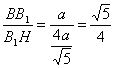 ,
,
即二面角B—A1N—B1的正切值为![]() . 2分
. 2分
(法二)(Ⅰ) 证明:建立如图所示空间直角坐标系,设AB=2a,AA1=a(a>0),则
A1(2a,0,a),B(2a,2a,0),C(0,2a,0),C1(0,2a,a). 2分
∵E为A1B的中点,M为CC1的中点,
∴E(2a,a,![]() ),M(0,2a,
),M(0,2a, ![]() ).
).
∴EM∥A1B1C1D1. 6分
(Ⅱ)解:设平面A1BM的法向量为n=(x,y,z),
又![]() =(0,2a,-a),
=(0,2a,-a),![]() =(-2a,0,
=(-2a,0,![]() ),
),
由n⊥![]() ,n⊥
,n⊥![]() ,得
,得
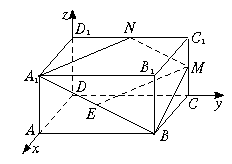
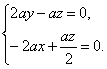
∴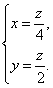
∴n=(![]() ,a).
9分
,a).
9分
而平面A1B1C1D1的法向量为n1=(0,0,1).
设二面角为θ,则cosθ=![]() .
.
又二面角为锐二面角,
∴cosθ=![]() . 11分
. 11分
从而tanθ=![]() 12分
12分
21.解:(Ⅰ)f′(x)=![]() +a,
2分
+a,
2分
由于f(x)在(0,1)上是增函数,
∴![]() +a>0在x∈(0,1)上恒成立,
+a>0在x∈(0,1)上恒成立,
∴a>-![]() 恒成立.
4分
恒成立.
4分
而-2<x-2<-1,
∴-1<![]() <-
<-![]() ,
,
∴![]() <-
<-![]() <1,
<1,
∴a≥1即为所求. 6分
(Ⅱ)(ⅰ)由题设知a1=c∈(0,1),
(ⅱ)假设0<ak<1,
当n=k+1时,由(Ⅰ)知f(x)=ln(2-x)+x在(0,1)上是增函数,
∴ak+1=ln(2-ak)+ak>0,且ak+1=ln(2-ak)+ak<1,得0<ak+1<1.
由(ⅰ)(ⅱ)得n∈N*时,0<an<1.
又∵an+1-an=ln(2-an)>0,
∴0<an<an+1<1,n∈N*. 9分
(Ⅲ)设![]() an=m,
an=m,
由an+1=ln(2-an)+an,得到
![]() an+1=
an+1=![]() [ln(2-an)+an].
[ln(2-an)+an].
即m=ln(2-m)+m,
∴m=1,即![]() an=1.
12分
an=1.
12分
22.解:∵y2=2(x+![]() ),
),
∴焦点为F(0,0),准线l:x=-1. 2分
设双曲线C存在,其离心率为e,点(x,y)为双曲线C上任意一点,
由条件![]() =e,得
=e,得
(1-e2)x2+y2-2e2x-e2=0. 4分
又设与x-y=0垂直的直线m为y=-x+b,
则双曲线C应与m有两个交点,设为A(x1,y1)、B(x2,y2),且AB=2![]() .
.
由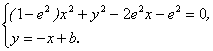
得(2-e2)x2-2(e2+b)x+b2-e2=0.
则 (*)成立,
(*)成立,
且x1+x2=![]() ,x1x2=
,x1x2=![]() . 9分
. 9分
又AB=2![]() ,所以2[(
,所以2[(![]() )2-4(
)2-4(![]() )]=8,
)]=8,
所以![]() =1.① 11分
=1.① 11分
又AB的中点M(![]() )在直线x-y=0上,
)在直线x-y=0上,
∴![]() .②
.②
由①、②解得![]()
此时(*)成立,所以满足条件的双曲线C存在,其方程为3x2-y2+8x+4=0. 14分
