湖北省名校第二次数学(理科)联考题
本试卷分第I卷和第Ⅱ卷两部分,共150分,考试时间120分钟
命题人:吴校红
第I卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合![]() ,
,
![]() ,那么P(2,3)∈A∩(CuB)的充要条件是
(
)
,那么P(2,3)∈A∩(CuB)的充要条件是
(
)
A. ![]() >-1且
>-1且![]() <5
B.
<5
B. ![]() <-1且
<-1且![]() <5
<5
C. ![]() >-1且
>-1且![]() >5
D.
>5
D. ![]() <-1且
<-1且![]() >5
>5
2. 已知![]() =
=![]() ,则
,则![]() 的值是
(
)
的值是
(
)
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
3. 若a、b、c是互不相等的实数,且a、b、c成等差数列,c、a、b成等比数列,则
a:b:c等于 ( )
A. (-2):1:4 B. 1:2:3 C. 2:3:4 D. (-1):1:3
4. 若直线![]() 始终平分圆
始终平分圆![]() 的周长,则
的周长,则![]() 的取值范围是
( )
的取值范围是
( )
A. (0,1) B. (0,1) C. (-∞,1) D. (-∞,1)
5. 设函数![]() ,若
,若![]() ,则
,则![]() 的值等于
(
)
的值等于
(
)
A. 2500
B. 50
C. 100 D.
2![]()
6. 设![]() ,则
,则![]() 展开式的第5项是
(
)
展开式的第5项是
(
)
A. 35i B. –21i C. 21 D. 35
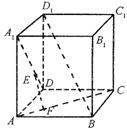 7. 在正方体ABCD—A1B1C1D1中,E、F分别在A1D、AC上,
7. 在正方体ABCD—A1B1C1D1中,E、F分别在A1D、AC上,
且A1E=![]() A1D,AF=
A1D,AF=![]() AC,则
(
)
AC,则
(
)
A. EF至多与A1D、AC之一垂直 B. EF是A1D、AC公垂线
C. EF与BD1相交 D. EF与BD1 异面
8. 口袋中有5只球,编号为1,2,3,4,5,从中任取3球,以![]()
表示取出的球的最大号码,则E![]() 等于
( )
等于
( )
9. 若![]() 定义:
定义:![]() ,例如
,例如
![]() ,则函数
,则函数![]() (
)
(
)
A.是偶函数不是奇函数 B.是奇函数不是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
10. 已知椭圆的离心率为![]() ,两焦点分别为F1,F2 ,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若
,两焦点分别为F1,F2 ,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若![]()
![]() ,则
,则![]() 的值为
(
)
的值为
(
)
 A.
A. ![]() B.
B.
![]() C.
C.
![]() D.
以上均不对
D.
以上均不对
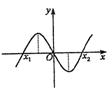
11.函数![]() 、
、![]() 且
且![]() 的图像如图所示,
的图像如图所示,
且![]() <0,则有
<0,则有
A.a>0,b>0 B.a<0,b<0
C.a<0,b>0 D.a>0,b<0
12. 一机器狗每秒钟前进或后退一步,程序设计师让机器狗以前进3步,再后退2步的规律移动,如果将此机器狗放在数轴的原点,方向正方向,以一步的距离为一个单位长, 令P(n)表示第n秒时机器狗所在位置的坐标,且P(0)=0,那么下列结论中错误的是
( )
A. P(3)= 3 B. P(5)= 1 C. P(101)= 21 D. P(103)< P(104)
第Ⅰ卷答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 答案 |
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.已知在整数集合内,关于![]() 的不等式
的不等式![]() <
<![]() 的解集为﹛1=,则实数
的解集为﹛1=,则实数![]() 的取值范围是
。
的取值范围是
。
14.若半径为R的球与正三棱柱的各个面相切,则球与正三棱柱的体积比是 。
15.把座位编号分别为1,2,3,4,5,6的六张电影票全部分给甲、乙、丙、丁四个人,每人至少分1张,至多分两张,且分得两张票必须是连号的,那么不同的分法种数是
。
16.已知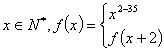
![]() ,其值域设为D,给出下列数值:-26,-1,9,14,27,65,则其中属于集合D的元素是
。(写出所有可能的数值)。
,其值域设为D,给出下列数值:-26,-1,9,14,27,65,则其中属于集合D的元素是
。(写出所有可能的数值)。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)已知向量![]() ,向量,
,向量,![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,且
,且![]() =-1
=-1
(1)求向量![]() ;
;
(2)设向量![]() =(1,0),向量
=(1,0),向量![]() ,其中0<
,其中0<![]() <
<![]() ,若
,若![]() =0,试求|
=0,试求|![]() ︱的取值范围。
︱的取值范围。
18.(本小题满分12分)设函数![]() 的图像关于原点对称,
的图像关于原点对称,![]() 的图像在点
的图像在点![]() 处的切线的斜率为-6,且当
处的切线的斜率为-6,且当![]() 时
时![]() 有极值。
有极值。
(1)
求![]() 、b、c、d的值;
、b、c、d的值;
(2)
若![]() 、
、![]() ,求证:︱
,求证:︱![]() ︱≤
︱≤![]() 。
。
19.(本小题满分12分)新上海商业城位于浦东陆家嘴金融贸易区中心地带,它由第一八
佰伴、时代广场等18幢高层商厦,10000平方米中心花园,九座天桥以及600米长的
环形步行街有机组成,是一座集购物、餐饮、娱乐、休闲、办公于一体的综合性、多功能的现代化商城,其中某一新建商场设有百货部、服装部和家电部三个经营部,共有190
名售货员,计划全商场日营业额(指每日卖出商品所收到的总金额)为60万元,根据经验,各部商品每l万元营业额所需售货员人数如表l,每1万元营业额所得利润情况如表2,商场将计划日营业额分配给三个经营部,同时适当安排各部的营业员人数,若商场预计每日的总利润为c(9≤c≤19.7)万元,商场分配给经营部的日营业额为正整数万元,问这个商场怎样分配日营业额给三个经营部?各部分别安排多少名售货员?
表1 各部每1万元营业额所需人数表 表2各部每1万元营业额所得利润表
| 部 门 | 利 润 |
| 百货部 | 0.3万元 |
| 服装部 | 0.5万元 |
| 家电部 | 0.2万元 |
| 部 门 | 人 数 |
| 百 货 部 | 5 |
| 服 装 部 | 4 |
| 家 电 部 | 2 |
 20.(本小题满分12分)如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1A2重合于A,且二面角A—DC—E为直二面角。
20.(本小题满分12分)如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1A2重合于A,且二面角A—DC—E为直二面角。
(1) 求证:CD⊥DE;
(2) 求AE与面DEC所成角的正弦值;
(3) 求点D到平面AEC的距离。
21.(本小题满分12分)如图,P是以F1、F2为焦点的双曲线C:![]() =1上的一点
=1上的一点
已知![]() =0,且∣
=0,且∣![]() ∣=2∣
∣=2∣![]() ∣.
∣.
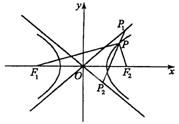
(1) 求双曲线的离心率![]() ;
;
(2) 过点P作直线分别与双曲线的两渐近线相交于
P1,P2两点,若![]() =
=![]()
![]() =0,
=0,
求双曲线C的方程。
22.(本小题满分14分)已知正项数列![]() 和
和![]() 中,
中,![]() 1 =
1 = ![]() (0<
(0<![]() <1=,
<1=,![]() .当
.当![]() ≥2时,
≥2时,![]() .
.
(1) 证明:对任意![]() 有
有![]() ;
;
(2) 求数列![]() 的通项公式;
的通项公式;
(3) 记![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() 的值.
的值.
数学(理科)参考答案
一、1.A 2.B 3.A 4.D 5.C 6.D 7.B 8.C 9.B 10.C 11.A 12.D
二、13. 2≤![]() <
<![]() 14.
14. ![]() 15.
144 16.–26,14,65
15.
144 16.–26,14,65
三、17.(1)令![]() ,则
,则![]()
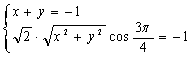 即
即![]()
![]() 或
或![]() ,故
,故![]() 或
或![]() (2)
(2)![]()
![]()
![]()
![]()
故
=![]()
=![]()
=![]()
![]()
![]() <
<![]() <
<![]()
![]() <
<![]() <
<![]()
则-1≤![]() <
<![]() ∴
∴![]() ≤
≤![]() <
<![]() 故
故![]() ≤
≤![]() <
<![]() .
.
18.(1)![]() 的图象关于原点对称,∴由
的图象关于原点对称,∴由![]() 恒成立有
恒成立有![]() .
.
则![]() 又
又![]()
∴![]()
![]()
![]() 故
故![]()
(2)![]()
![]() <0,
<0,![]() 在
在
[-1,1]上递减而![]() ∴
∴![]() ≤
≤![]() ≤
≤![]() 即
即![]() ≤
≤![]() ≤
≤![]() ∴
∴![]() ≤
≤![]() 同理可得
同理可得![]() ≤
≤![]() ∴
∴![]() ≤
≤![]() +
+![]() ≤
≤![]() 故
故![]() ≤
≤![]() .
.
|
|
|
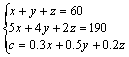 由 ①②消去z得:
由 ①②消去z得:![]()
![]() ≤c≤19.7 ∴8≤
≤c≤19.7 ∴8≤![]() ≤10 而
≤10 而 ![]() ∴
∴![]() 或
或![]()
故该商场分配营业额及各部售货员人数的方案有两种,分别为:
方案1: 方案2:
| 部 门 | 营业额 | 人 数 |
| 百 货 部 | 10 | 50 |
| 服 装 部 | 20 | 80 |
| 家 电 部 | 30 | 60 |
| 部 门 | 营业额 | 人 数 |
| 百 货 部 | 8 | 40 |
| 服 装 部 | 23 | 92 |
| 家 电 部 | 29 | 58 |
20. (1)∵A1、A2重合于A
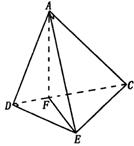 ∴AC⊥AD,AC⊥AE,故AC⊥面ADE ∴AC⊥DE
∴AC⊥AD,AC⊥AE,故AC⊥面ADE ∴AC⊥DE
∵A-DC-E为直二面角, ∴过A作AF⊥CD于F,则AF⊥面CDE,
故CD为AC在面CDE上的射影,由三垂线定理的逆定理有:CD⊥DE.
(2)∵AF⊥面CDE,∴∠AEF为AE与面DEC所成的角,
在Rt△CAD中,AD=2,AC=4,∴DC=2![]() ,AF=
,AF=![]() ,
,
又∵CD⊥DE,∴在正方体A1BA2C中,△DBE~△CA1D
故![]() ,∴DE=
,∴DE=![]() 又∵DE⊥CD,DE⊥AC,∴DE⊥面ACD,则
又∵DE⊥CD,DE⊥AC,∴DE⊥面ACD,则
DE⊥AD,∴在Rt△ADE中,AE=3,故在Rt△AFE中,![]() ∴AE与面DEC所成角的正弦值为
∴AE与面DEC所成角的正弦值为![]() .
.
(3)设D到面AEC的距离为d,则由VD—AEC=VA—DEC有:![]()
∴3×4d=2![]() 故
故![]() ,即点D到平面AEC的距离为
,即点D到平面AEC的距离为![]() .
.
21.(1)由![]() 得
得![]() ,即△F1PF2为直角三角形.
,即△F1PF2为直角三角形.
设![]() ,则
,则![]() 于是有(2r)2+r2=4c2和2r-r=2a
于是有(2r)2+r2=4c2和2r-r=2a![]() 5×(2a)2=4c2
5×(2a)2=4c2![]() e=
e=![]() .
.
则![]() ①
①
由![]() 得
得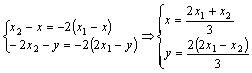
∵点![]() 在双曲线
在双曲线![]() 上,∴
上,∴![]() ,又
,又![]() .
.
∴上式为![]() . 简化得:
. 简化得:![]() ②
②
由①②得a2=2,从而得b2=8. 故所求双曲线方程为![]() .
.
22.(1)证明:用数学归纳法证明.
① 当n=1时,a1+b1=a+(1-a)=1,命题成立:②假设n=k(k≥1且![]() )时命题成立,即ak+bk=1,
)时命题成立,即ak+bk=1,
则当![]() 时,
时,![]() =
=![]() .
.
∴当![]() 时,命题也成立.综合①、②知,
时,命题也成立.综合①、②知,![]() 对
对![]() 恒成立.
恒成立.
(2)解;∵![]() ∴
∴![]() ,即
,即![]() ③ ∴数列
③ ∴数列![]() 是公差为1的等差数列,其首项是
是公差为1的等差数列,其首项是![]() ∴
∴![]() ,从而
,从而![]() .
.
(3)解:∵![]() , ③式变形为
, ③式变形为![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() .
.