江华一中06届高三四月第二次月考文科数学试题
一、选择题(每小题5分,共50分)
1、已知两点P(4,-9)、Q(-2,3),则直线PQ与y轴的交点分![]() 的比为
的比为
A、![]() B、
B、![]() C、2 D、3
C、2 D、3
2、已知全集为U,若集合M、N是U的真子集,且同时满足:![]() ,
,
![]() ,则下列关系式不成立的是
,则下列关系式不成立的是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、某人射击命中目标的概率为0.6,每次射击互不影响,连续射击3次,至少有2次命中目标的概率为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知函数f(x)为奇函数,并且对任意![]() ,当
,当![]() 时,恒有
时,恒有![]() >0,则
>0,则
A、f(3)>f(-5) B、f(-3)<f(-5) C、f(-5)>f(3) D、f(-3)>f(-5)
5、已知双曲线![]() 的左支上一点M到右焦点F1的距离为18,点N是MF1的中点,O为坐标原点,则|ON|等于
的左支上一点M到右焦点F1的距离为18,点N是MF1的中点,O为坐标原点,则|ON|等于
A、4 B、2 C、1 D、![]()
6、要得到函数![]() 的图象,且使平移的距离最短,则需将函数
的图象,且使平移的距离最短,则需将函数
![]() 的图象
的图象
A、向左平移![]() 个单位
B、向右平移
个单位
B、向右平移![]() 个单位
个单位
C、向左平移![]() 个单位 D、向右平移
个单位 D、向右平移![]() 个单位
个单位
7、设{an}是公差为-2的等差数列,如果a1+a4+a7+…+a28=90,那么a3+a6+a9+…+a30的值为
A、80 B、60 C、50 D、70
8、若函数![]() 的定义域为
的定义域为![]() ,则实数a的取值范围是
,则实数a的取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
 9、设M=
9、设M=![]() ,且a+b+c=1(a、b、c∈R+),则M的取值范围是
,且a+b+c=1(a、b、c∈R+),则M的取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
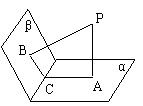
10、已知二面角![]() 的平面角为θ,PA⊥α,PB⊥β,
的平面角为θ,PA⊥α,PB⊥β,
A、B为垂足,且PA=4,PB=5,设A、B到二面角
的棱的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的
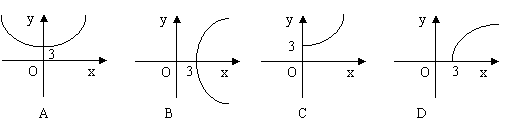 |
二、填空题(每小题4分,共20分)
11、某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2:3:4,现用分层抽样的方法抽取一个容量为n的样本,样本中A种型号的产品有16件,那么此样本的容量n=
12、不等式![]() 的解集是
的解集是
13、函数![]() 的导函数
的导函数![]() 在区间[0,1]上存在反函数的充要条件是
在区间[0,1]上存在反函数的充要条件是
14、如果把圆C:![]() 沿向量
沿向量![]() 平移后得到圆
平移后得到圆![]() ,且
,且![]() 与直线3x-4y=0相切,则m的值为
与直线3x-4y=0相切,则m的值为
15、已知![]() ,若b: a=3:1,则
,若b: a=3:1,则![]() 的展开式中系数最大的项是
的展开式中系数最大的项是
三、解答题(共80分)
16、(12分)设![]() 是关于x的不等式
是关于x的不等式![]() 的整数解
的整数解
Ⅰ)求数列![]() 的通项公式
的通项公式![]() ;
;
Ⅱ)设![]() ,求证:
,求证:![]()
17、(本题满分12分)设已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的值.
的值.
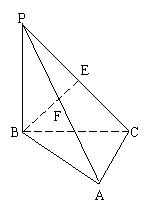
18、(14分)如图,在三棱锥P-ABC中,PB⊥底面ABC,AC⊥BC,PB=AC=2,AP与侧面PBC所成的角的正切值为![]() ,E为PC的中点
,E为PC的中点
Ⅰ)求证:侧面PAC⊥侧面PBC;
Ⅱ)求二面角E-AB-C的余弦值
Ⅲ)若F在PA上运动,当AF为何值时,体积![]()
 |
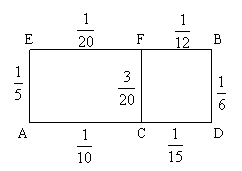
![]() 19、(14分)某先生居住在城市A处,准备开车到单位B处上班,根据实际情况分析可知该地各路段发生堵车事件是互不影响的,且在同一路段发生堵车事件最多一次,交通部门发布的发生堵车事件的概率信息如下图表示。(例如路线A C D为两路段AC和CD,路段AC发生堵车的概率为
19、(14分)某先生居住在城市A处,准备开车到单位B处上班,根据实际情况分析可知该地各路段发生堵车事件是互不影响的,且在同一路段发生堵车事件最多一次,交通部门发布的发生堵车事件的概率信息如下图表示。(例如路线A C D为两路段AC和CD,路段AC发生堵车的概率为![]() ,路段CD发生堵车的概率为
,路段CD发生堵车的概率为![]() )
)
![]() Ⅰ)求路线A C F B恰好堵车两次的概率;
Ⅰ)求路线A C F B恰好堵车两次的概率;
Ⅱ)求路线A E F B至少堵车一次的概率
 |
20、(14分)已知向量![]() =(2,0),
=(2,0),![]() =
=![]() =(0,1),动点M到定直线
=(0,1),动点M到定直线
y=1的距离为d,且满足![]() ,其中O为坐标原点,k≥0为常数
,其中O为坐标原点,k≥0为常数
Ⅰ)求动点M的轨迹方程,并指明曲线的类型;
Ⅱ)当![]() 时,求
时,求![]() 的取值范围
的取值范围
21、(14分)已知曲线![]() 在点P(x,y)处的切线的斜率为k(x),若k(-1)=0,且对一切实数x,不等式
在点P(x,y)处的切线的斜率为k(x),若k(-1)=0,且对一切实数x,不等式![]() 恒成立
恒成立
Ⅰ)求函数k(x)的表达式;
Ⅱ)若![]() 对一切实数x∈[0,2]恒成立,求实数λ的取值范围
对一切实数x∈[0,2]恒成立,求实数λ的取值范围
参考答案
一、CDBDA CCBDD
二、11、72 12、![]() 13、
13、![]()
14、![]() 15、
15、![]()
16、Ⅰ)![]() Ⅱ)用错位相减法
Ⅱ)用错位相减法
17、Ⅰ)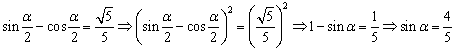 ;
;
Ⅱ)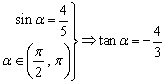 ,由此及
,由此及![]() 得
得
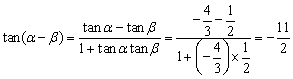
18、Ⅱ)![]() Ⅲ)
Ⅲ)![]()
19、Ⅰ)![]() Ⅱ)
Ⅱ)![]()
20、Ⅰ)![]()
![]() 时,为圆
时,为圆
![]() 时,为焦点在x轴上的椭圆
时,为焦点在x轴上的椭圆
![]() 时,为直线x=0
时,为直线x=0
![]() >1时,为焦点在x轴上的双曲线
>1时,为焦点在x轴上的双曲线
Ⅱ)![]()
21、Ⅰ)![]()
Ⅱ)![]()