高三文科复习作业(7)
班级 姓名 座号
1、若![]() 的值等于 (
)
的值等于 (
)
A.1 B.![]() C.
C.![]() D.3
D.3
2、设![]() 展开式中含
展开式中含![]() 项的系数,则
项的系数,则![]() 等于( )
等于( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
3、右图中的(1)、(2)分别表示二次函数![]() 和分段函数
和分段函数![]() 的部分图象,
的部分图象,![]() ,则函数
,则函数![]() 的最大值是 ( )
的最大值是 ( )
A.7 B.9 C.10 D.12
4、平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足
![]() ,点c的轨迹方程为
(
)
,点c的轨迹方程为
(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5、袋里装有大小相同的黑、白两色的手套,黑色手套15只,白色手套10只.现从中随机地取出两只手套,如果两只是同色手套则甲获胜,两只手套颜色不同则乙获胜. 试问:甲、乙获胜的机会是 ( )
A. 甲多 B. 乙多 C. 一样多 D. 不确定的
6、若以圆锥曲线的一条经过焦点的弦为直径的圆与对应的准线无公共点,则此圆锥曲线为( )
A.双曲线 B.椭圆 C.抛物线 D.椭圆或双曲线
 7、右图是一次数学考试成绩的样本频率分布直方图(样本容量n=200),若成绩在60分以上为及格,则样本中及格人数是
7、右图是一次数学考试成绩的样本频率分布直方图(样本容量n=200),若成绩在60分以上为及格,则样本中及格人数是
 8、一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示。(至少打开一个水口)
8、一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示。(至少打开一个水口)
给出以下![]() 个论断:①
个论断:①![]() 点到
点到![]() 点只进水不出水;②
点只进水不出水;②![]() 点到
点到![]() 点不进水只出水;③
点不进水只出水;③![]() 点到
点到![]() 点不进水不出水.则一定不确定的论断是__________.
点不进水不出水.则一定不确定的论断是__________.
8、已知函数![]() 的图象在点P(1,0)处的切线与直线
的图象在点P(1,0)处的切线与直线![]() 平行.
平行.
(1)求a、b的值; (2)求函数![]() 的单调区间; (3)求函数
的单调区间; (3)求函数![]() 在区间[0,t](t>0)上的最小值和最大值.
在区间[0,t](t>0)上的最小值和最大值.
4、已知等差数列![]() 是其前n项和且S20=610. (I)求数列
是其前n项和且S20=610. (I)求数列![]() 的通项公式;
的通项公式;
(II)若从数列![]() 中依次取出第2项,第4项,第8项,……,第2n项,按原来的顺序组成一个新数列
中依次取出第2项,第4项,第8项,……,第2n项,按原来的顺序组成一个新数列![]() ,求数列
,求数列![]() 的前n项和Tn.
的前n项和Tn.
作业(7)答案1、D 2、C 3、A 4、D 5、C 6、B 7、80 8、②③
9\解:(1)∵P(1,0)在![]() 的图象上,∴0=1+a+b.
的图象上,∴0=1+a+b.
又![]() ,……………………………………2分
,……………………………………2分
![]() ……………………4分
……………………4分
(2)![]() ………………6分
………………6分
![]() 分别在
分别在![]() 上是增函数,在[0,2]上是减函数.…………8分
上是增函数,在[0,2]上是减函数.…………8分
(3)若![]() 在区间[0,t]
在区间[0,t]![]() 上是减函数,
上是减函数,
当![]() 时,
时,![]() ………………9分
………………9分
若![]() 在区间[0,2]上是减函数,在(2,3
在区间[0,2]上是减函数,在(2,3![]() 上是增函数,
上是增函数,
且![]() 当
当![]() 或
或![]() 时,
时,![]() ,……………………10分
,……………………10分
当![]()
若![]() 在区间[0,2]上是减函数,在(2,t
在区间[0,2]上是减函数,在(2,t![]() 上是增函数
上是增函数
且![]() 当
当![]() ;
;
当![]() 时
时![]() ……………………………………………………12分
……………………………………………………12分
10\(1)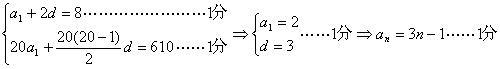
(2)![]() ……………………………………………………………………2分
……………………………………………………………………2分
![]() (21+22+23+…+2n)-n…2分
(21+22+23+…+2n)-n…2分
=6(2n-1)-n…………………………2分
