08届高考数学第五次模拟考试
数学试卷(理科)
A卷
一、选择题(本大题共12小题,每小题5分,共计60分)
1.
计算:![]() ( )
( )
A.![]() B.
B.![]() C.1
D.-1
C.1
D.-1
2.已知集合![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设随机变量服从正态分布![]() 则
则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.![]() 和直线
和直线![]() 垂直的 ( )
垂直的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
5.地球半径为R,在北纬30°的圆上,A点经度为东经120°,B点的经度为西经60°,
则A、B两点的球面距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 的反函数是
( )
的反函数是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.直线![]() 上的点到圆
上的点到圆![]() 上的点的最近距离是 ( )
上的点的最近距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
8.将函数![]() R)的图象上所有的点向左平行移动
R)的图象上所有的点向左平行移动![]() 个单位长度,再把图象
个单位长度,再把图象
上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.若不等式组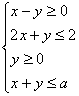 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
A.(![]() ) B.
) B.![]() C.(1,2) D.(
C.(1,2) D.(![]() )
)
11.由0,1,2,3这四个数字组成的四位数中,有重复数字的四位数共有 ( )
A.168个 B.174个 C.232个 D.238个
12.已知向量![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 的夹角为( )
的夹角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B卷
|
二、填空题(本大题共4小题,每小题5分,共计20分)
13.![]() 的展开式中,含
的展开式中,含![]() 项的系数
.
项的系数
.
14.抛物线![]() 的准线方程是
的准线方程是![]() ,则
,则![]() 的值为
.
的值为
.
15.等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 则公比
则公比![]() .
.
16.关于正四棱锥![]() ,给出下列命题:
,给出下列命题:
1异面直线![]() 与
与![]() 所成的角为直角;
所成的角为直角;
2侧面为锐角三角形;
3侧面与底面所成的二面角大于侧棱与底面所成的角;
4相邻两侧面所成的二面角为钝角。
其中正确命题的序号是 .
三、解答题(本大题共6小题,共计70分)
17.(本小题满分10分)已知函数![]() 。
。
(Ⅰ)当![]() 时,求
时,求![]() 的单调递增区间:
的单调递增区间:
(Ⅱ)当![]() ,且
,且![]() 时,
时,![]() 的值域是
的值域是![]() ,求
,求![]() 的值。
的值。
18.(本小题满分12分)
袋中装有大小相等的3个白球,2个红球和![]() 个黑球,现从中任取2个球,每取得一个白球得1分,每取得一个红球得2分,每取得一个黑球0分,用
个黑球,现从中任取2个球,每取得一个白球得1分,每取得一个红球得2分,每取得一个黑球0分,用![]() 表示所得分数,已知得0分的概率为
表示所得分数,已知得0分的概率为![]() 。
。
(Ⅰ)袋中黑球的个数![]() ;
;
(Ⅱ)![]() 的概率分布列及数学期望
的概率分布列及数学期望![]() 。
。
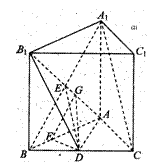
19.(本小题满分12分)
如图,正三棱柱![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]()
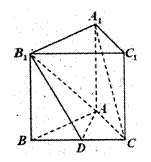 (Ⅰ)求证:
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
20.(本小题满分12分)
设![]() 分别是椭圆的
分别是椭圆的![]() 左,右焦点。
左,右焦点。
(Ⅰ)若![]() 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且![]()
![]() ,
,
求点![]() 的坐标。
的坐标。
(Ⅱ)设过定点![]() 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围。
的取值范围。
21.(本小题满分12分)
已知:![]()
(Ⅰ)求![]()
![]()
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)求证:![]()
22.(本小题满分12分)
已知函数![]() ,设
,设![]() 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以![]() 图象上任意一点
图象上任意一点![]() 为切点的切线的斜率
为切点的切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的最小值。
的最小值。
(Ⅲ)是否存在实数![]() ,使得函数
,使得函数![]() 的图象与
的图象与![]() 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出![]() 的取值范围,若不存在,说名理由。
的取值范围,若不存在,说名理由。
参考答案
一、选择题(本大题共4小题,每小题5分,共计20分
1.C 2.D 3.C 4.A 5.D 6.A 7.C 8.B 9.D 10.D 11.B 12.A
|
13.840 14.-![]() 15.2或
15.2或![]() 16.1234
16.1234
三、解答题 (本大题共6小题,共计70分)
17.(本小题满分10分)
解:(Ⅰ)![]() ,
,
![]() ……………………4分
……………………4分
(Ⅱ)![]()
![]() …………6分
…………6分
而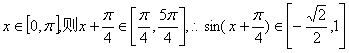 …………8分
…………8分
故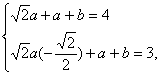
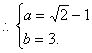 ………………………………10分
………………………………10分
18.(本小题满分12分)
解:(Ⅰ)![]() , …………………………………………3分
, …………………………………………3分
![]() 即袋中有4个黑球。 …………5分
即袋中有4个黑球。 …………5分
(Ⅱ)![]() 0, 1, 2, 3, 4。
0, 1, 2, 3, 4。
![]() ,
,![]()
![]() ,
, ![]() ……………………8分
……………………8分
![]()
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
![]() …………………………12分
…………………………12分
19.(本小题满分12分)
解法一:(Ⅰ)证明:连接![]()
![]()
![]()
![]()
![]()
![]() ∥
∥![]() 。 ……………………3分
。 ……………………3分
![]()
![]() ∥平面
∥平面![]() …………………………5分
…………………………5分
(Ⅱ)解:在平面![]()
![]()
![]()
![]()
![]() —
—![]() —
—![]() ……………………8分
……………………8分
设![]() 。
。
在![]()
所以,二面角![]() —
—![]() —
—![]() 的大小为
的大小为![]() 。 ………………12分
。 ………………12分
解法二:建立空间直角坐标系![]() —
—![]() ,如图,
,如图,
(Ⅰ)证明:连接![]() 连接
连接![]() 。设
。设![]()
 则
则![]()
![]()
![]()
![]() ∥
∥![]() 。 …………………………3分
。 …………………………3分
![]() ∥平面
∥平面![]() …………5分
…………5分
(Ⅱ)解:![]()
设![]()
故 ![]()
同理,可求得平面![]() 。………………9分
。………………9分
设二面角![]() —
—![]() —
—![]() 的大小为
的大小为![]()
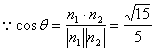
![]()
![]()
![]() 的大小为
的大小为![]() 。……………………12分
。……………………12分
20.(本小题满分12分)
解:(Ⅰ)易知![]() 。
。
![]()
![]() ,
,
………………………………3分
联立![]()
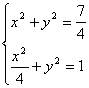 ,解得
,解得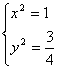
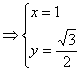 ,
,![]() ………………5分
………………5分
(Ⅱ)显然![]() …………………………………………6分
…………………………………………6分
可设![]()
联立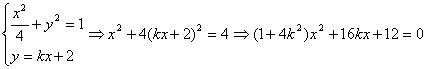
![]() ……………………………………7分
……………………………………7分
由![]()
![]()
得![]() 1 …………………………………………8分
1 …………………………………………8分
又![]() ,
,
![]() ………………………………………………9分
………………………………………………9分
又![]()
![]()
![]()
![]() 2 ……………………………………11分
2 ……………………………………11分
综12可知![]() …………12分
…………12分
21.(本小题满分12分)
解:(Ⅰ)由已知![]() ……………………………………1分
……………………………………1分
![]() ,所以,
,所以,![]() ……3分
……3分
(Ⅱ)![]()
![]()
所以对于任意的![]() …………………………7分
…………………………7分
(Ⅲ)![]()
![]() 1
1
![]() 2
2
1—2,得
![]() …………9分
…………9分
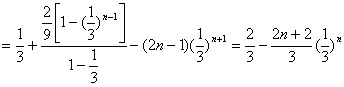
![]() …………11分 又
…………11分 又![]() …………12分
…………12分
22.(本小题满分12分)
解.(Ⅰ) ![]()
![]()
![]()
![]()
由![]() 。
。
![]()
(Ⅱ)![]()
![]() 当
当![]()
![]() …………………………………………4分
…………………………………………4分
(Ⅲ)若![]() 的图象与
的图象与
![]() 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即![]() 有四个不同的根,亦即
有四个不同的根,亦即
![]() 有四个不同的根。
有四个不同的根。
令![]() ,
,
则![]() 。
。
当![]() 变化时
变化时![]() 的变化情况如下表:
的变化情况如下表:
|
|
| (-1,0) | (0,1) | (1, |
|
| + | - | + | - |
|
| ↗ | ↘ | ↗ | ↘ |
由表格知:![]() 。
。
画出草图和验证![]() 可知,当
可知,当![]() 时,
时,
![]()
![]()
![]()
![]() ………………4分
………………4分