|
一、 高考分析
1、 分值、题型、难度设置
圆锥曲线是高中数学的重要内容之一,分值约占14﹪,即20分左右,题型一般为二小一大,例如,2005年高考为一道选择题,一道填空题 一道解答题。小题基础灵活,解答题一般在中等以上,一般具有较高的区分度。
考试内容:椭圆、双曲线、抛物线的定义,标准方程,简单的几何性质,椭圆的参数方程。
主要题型:(1)定义及简单几何性质的灵活运用;(2)求曲线方程(含指定圆锥曲线方程及轨迹方程);(3)直线与圆锥曲线的位置关系问题(交点、弦长、中点弦及斜率、对称问题),确定参数的取值范围;(4)在导数、不等式、函数、向量等知识网络交汇点上的问题。
2、 命题方向
解析几何内容多,范围广,综合度高,其特点是:数形结合,形象思维,规律性强,运算量大,综合性好。主要考察运算能力,逻辑思维能力,以及分析问题和解决问题的综合能力。
涉及函数、方程、不等式、三角、向量和导数等方面的内容,以及数形结合、分类讨论、等价转化等数学思想方法。
要注意一些立意新,角度好,有创意的题目,特别要关注在向量和解析几何交汇点上的命题趋势,两者通过坐标自然融合,既考查基础知识、基本方法,又平淡之中见功夫,强化区分功能,突出对能力的考查,从不同的思维层次上考察能力,有较好的思维价值。
二、 专题复习
2.1考查直线和圆锥曲线方程等有关基础知识和基本方法,要特别重视圆锥曲线定义的灵活应用,反映思维品质。
例1.1)如图,在正方体![]() 的侧面
的侧面![]() 内有
内有
动点![]() 到直线
到直线![]() 与直线
与直线![]() 距离相等,则动点
距离相等,则动点![]() 所在的曲线的形状为:( )
所在的曲线的形状为:( )
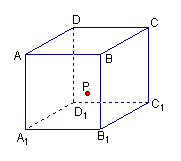
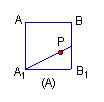
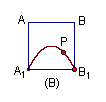
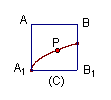
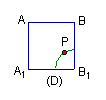
分析:本题主要考查抛物线定义,线面垂直关系及点到直线的距离等概念,情景新,角度好,有创意,考查基础知识和基本方法。
∵![]() ⊥面
⊥面![]() ,
,![]() 即为点
即为点![]() 到直线
到直线![]() 的距离,故动点
的距离,故动点![]() 的轨迹应为过
的轨迹应为过![]() 中点的抛物线,又点
中点的抛物线,又点![]() 显然在此抛物线上,故选
显然在此抛物线上,故选![]() 。
。
2)已知F1、F2是双曲线![]() 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是( )
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.2 求曲线的方程,考查坐标法的思想和方法,从不同思维层次上反映数学能力。
例2 双曲线![]() 为渐近线且过点
为渐近线且过点![]() 。
。
(1) 求双曲线![]() 的方程;
的方程;
(2) 已知动点![]() 与曲线
与曲线![]() 的两个焦点所连线段长的和为定长,且这两条线段夹角的余弦最小值为
的两个焦点所连线段长的和为定长,且这两条线段夹角的余弦最小值为![]() ,求动点
,求动点![]() 的轨迹方程;
的轨迹方程;
(3) 在![]() 轴正半轴上是否存在一点
轴正半轴上是否存在一点![]() ,使得
,使得![]() 与
与![]() 的轨迹方程上的点的最短距离为1?若存在,求出
的轨迹方程上的点的最短距离为1?若存在,求出![]() 点坐标;若不存在,说明理由。
点坐标;若不存在,说明理由。
分析:本题主要考查双曲线、椭圆的方程,基本不等式及二次函数的最值,利用待定系数法可求出指定圆锥曲线的方程。本题把最值问题联系起来,体现了知识的整体性和系统性,既考查基础知识和基本方法,又渗透数学思想,突出对能力的考查,从不同的思维层次上反映能力。
(Ⅰ)设双曲线方程为![]() ,故
,故![]()
(Ⅱ)由题意,![]() 点轨迹以
点轨迹以![]() 为焦点的椭圆,设方程为:
为焦点的椭圆,设方程为:![]() ,则
,则![]() ①
①
记![]()
![]() ,则
,则![]() ,
,
由![]() 知当
知当![]() 即P为椭圆短轴端点时,
即P为椭圆短轴端点时,![]() 有最小值,并且
有最小值,并且![]() ②,由①,②可得
②,由①,②可得![]() ,故动点P的轨迹方程为:
,故动点P的轨迹方程为:![]() 。
。
(Ⅲ)设![]() 是以上轨迹上任一点,则
是以上轨迹上任一点,则![]() ,
,![]() ,又
,又![]() ,
,
对称轴![]() 。
。
(1)若![]() 即
即![]() ,则当
,则当![]() 时,
时,![]()
![]() ,不合。
,不合。
(2)若![]() ,即
,即![]() ,则当
,则当![]() 时,
时,![]()
![]() 或
或![]() 。
。
故存在点![]() 或
或![]() 满足条件。
满足条件。
2.3 有关直线和圆锥曲线的位置关系问题,主要涉及求参数的值或范围,既考基础,又考能力,突出区分功能,体现思维价值。
例3 过椭圆C:![]() 上动点P作⊙
上动点P作⊙![]() :
:![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,若直线
,若直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点;
两点;
(1) 求证: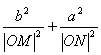 为定值;
为定值;
(2) 若椭圆C上存在点![]() ,使得由
,使得由![]() 向⊙
向⊙![]() 所引两条切线互相垂直,求离心率的取值范围。
所引两条切线互相垂直,求离心率的取值范围。
分析:本题主要考查直线与圆的方程,以及离心率的概念,立意新,思维活,在考查基础知识的同时突出对理性思维能力的考查。
(1) 设![]() 易知
易知![]() 四点共圆,并且此圆的方程为
四点共圆,并且此圆的方程为![]() ,由于
,由于![]() 为上述圆与已知圆
为上述圆与已知圆![]() 得
得![]() ,令
,令![]() 得
得![]() ,故
,故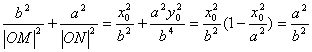 (定值)。
(定值)。
注意 :本小题切点弦![]() 的直线方程也可用“设而不求”的方法得出。
的直线方程也可用“设而不求”的方法得出。
(2)由题意,四边形![]() 为正方形,
为正方形,![]() ,从而存在点
,从而存在点![]() 的条件为:以
的条件为:以![]() 为圆心、
为圆心、![]() 为半径的圆与椭圆相交,
为半径的圆与椭圆相交,![]() ,故
,故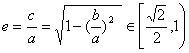 。
。
例4 已知顶点在原点,焦点在![]() 轴上的抛物线
轴上的抛物线![]() 截直线
截直线![]() 所得的弦长为
所得的弦长为![]() 。
。
(1) 求抛物线C的方程;
(2) 过点![]() ,且斜率
,且斜率![]() 的直线与抛物线C相交与A、B两点,求M分
的直线与抛物线C相交与A、B两点,求M分![]() 所成比
所成比![]() 的范围。
的范围。
分析 本题涉及直线与抛物线的位置关系问题,主要考查一元二次方程与系数关系,两点间距离公式及点M分![]() 所成的比等基础知识和基本方法,考查综合分析和解决问题的能力,具有较好的思维价值。
所成的比等基础知识和基本方法,考查综合分析和解决问题的能力,具有较好的思维价值。
(1) 设![]() ,直线与抛物线C交于
,直线与抛物线C交于![]() ,由
,由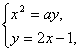
得![]() ,即
,即![]()
而![]()
![]() ,
,
![]() 即
即![]() 解得
解得![]() 或
或![]() ,
,
故![]() 。
。
(2)直线![]() 把它代入
把它代入![]() 得
得![]() ∵
∵![]()
![]() 不合。把
不合。把![]() 代入
代入![]() ,设
,设![]() ,
,
![]() ,则
,则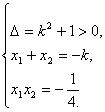 (*) 由定比分点公式:0=
(*) 由定比分点公式:0=![]() ,
,![]() 代入(*)的
代入(*)的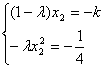 ,显然
,显然![]() 又
又![]() ,于是
,于是![]() 即
即![]() 故
故![]()
2.4 重视在导数、向量、函数、不等式等知识交汇点上的命题趋势,既考查相关的知识,又体现知识间的联系和应用,突出对知识的迁移和应用能力的考查。
例5 已知椭圆的中心在原点,离心率为,一个焦点是F(-m,0)(m是大于0的常数).
(Ⅰ)求椭圆的方程;
(Ⅱ)设Q是椭圆上的一点,且过点F、Q的直线![]() 与y轴交于点M. 若
与y轴交于点M. 若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
分析:本小题主要考查直线、椭圆和向量等基本知识,以及推理能力和运算能力.
(I)设所求椭圆方程是![]()
由已知,得 ![]() 所以
所以![]() .
.
故所求的椭圆方程是![]()
(II)设Q(![]() ),直线
),直线![]()
当![]() 由定比分点坐标公式,得
由定比分点坐标公式,得

![]() .
.
于是![]() 故直线l的斜率是0,
故直线l的斜率是0,![]() .
.
例6 设![]() 曲线
曲线![]() 在点
在点![]() 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为![]() ,则
,则![]() 到曲线
到曲线![]() 对称轴距离的取值范围是( )
对称轴距离的取值范围是( )
(A)![]() (B
(B![]() )
(C
)
(C![]() )
(D)
)
(D) ![]()
分析: 本题主要考查导数的求法,倾斜角和斜率的概念,点到直线的距离等知识。
∵ ![]() 过P点的切线斜率
过P点的切线斜率![]() 由题意:
由题意:![]()
即![]()
![]() 又
又![]() ∵
∵![]() 的对称轴为
的对称轴为![]()
![]() 到该对称轴的距离为
到该对称轴的距离为![]()
![]() ,故应选B.
,故应选B.
例7 已知常数![]() ,向量
,向量![]() ,经过原点O以
,经过原点O以![]()
![]() 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中![]() 。试问:是否存在两个定点
。试问:是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
分析: 本题依托向量把解析几何联系起来,既考查向量的坐标运算,又考查直线与曲线的方程及圆锥曲线的定义和简单的几何性质。解本题的关键是求出![]() 点轨迹方程。
点轨迹方程。
∵![]()
![]() ,
,![]() 直线OA和AP的方程分别为:
直线OA和AP的方程分别为:
![]() 消去参数
消去参数![]() 得P点的轨迹方程为:
得P点的轨迹方程为:![]() ,整理得
,整理得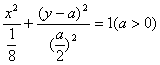 (*)
(*)
(1) 当![]() 时,方程(*)表示圆,故不存在满足题意的两定点E和F;
时,方程(*)表示圆,故不存在满足题意的两定点E和F;
(2) 当![]() 时,方程(*)表示焦点在
时,方程(*)表示焦点在![]() 上的椭圆,两焦点
上的椭圆,两焦点![]() 和
和![]() 即为满足题意的两定点;
即为满足题意的两定点;
(3) 当![]() 时,方程(*)表示焦点在
时,方程(*)表示焦点在![]() 轴上的椭圆,两焦点
轴上的椭圆,两焦点![]() 和
和![]() 即为满足题意的两定点。
即为满足题意的两定点。
例8已知椭圆C:![]() +
+![]() =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线
l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设![]() =λ
=λ![]() .
.
(Ⅰ)证明:λ=1-e2;
(Ⅱ)确定λ的值,使得△PF1F2是等腰三角形.
(Ⅰ)证法一:因为A、B分别是直线l:![]() 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是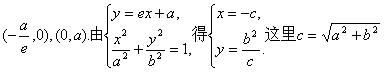 .
.
所以点M的坐标是(![]() ). 由
). 由![]()
即
解法二:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有PF1=F1F2,
设点P的坐标是![]() ,
,
则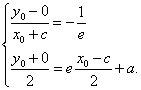 ,
,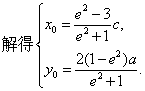
由PF1=F1F2得![]()
两边同时除以4a2,化简得![]()
从而![]()
于是![]()
![]()
即当![]() 时,△PF1F2为等腰三角形
时,△PF1F2为等腰三角形![]()
例9.如图,设抛物线![]() 的焦点为F,动点P在直线
的焦点为F,动点P在直线![]() 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
解:(1)设切点A、B坐标分别为![]() ,
,
∴切线AP的方程为:![]()
切线BP的方程为:![]()
解得P点的坐标为:![]()
所以△APB的重心G的坐标为 ![]() ,
,
![]()
所以![]() ,由点P在直线l上运动,从而得到重心G的轨迹方程为:
,由点P在直线l上运动,从而得到重心G的轨迹方程为:
![]()
(2)方法1:因为![]()
由于P点在抛物线外,则![]()
∴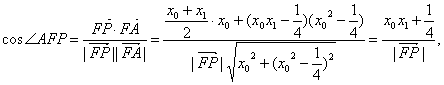
同理有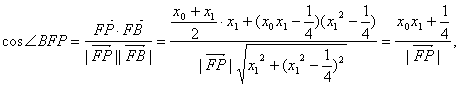
∴∠AFP=∠PFB.
方法2:①当![]() 所以P点坐标为
所以P点坐标为![]() ,则P点到直线AF的距离为:
,则P点到直线AF的距离为:
即![]()
所以P点到直线BF的距离为: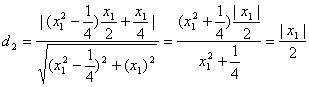
所以d1=d2,即得∠AFP=∠PFB.
②当![]() 时,直线AF的方程:
时,直线AF的方程: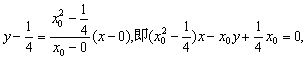
直线BF的方程:
所以P点到直线AF的距离为:
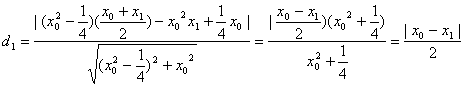 ,同理可得到P点到直线BF的距离
,同理可得到P点到直线BF的距离![]() ,因此由d1=d2,可得到∠AFP=∠PFB
,因此由d1=d2,可得到∠AFP=∠PFB![]()
2005年11月