高考题型与方法研究------函数与函数思想

【例题选讲】

1、设全集，集合，，那么集合 等于（　 ）

（A）　 （B）　 （C）　 （D）

2、函数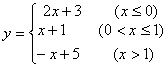，的最大值是 　　　　 。

3、已知，则的最大值是 　　　　 。

4、已知函数，定义在R上的奇函数，当时，，则的表达式是 　　　　 。

5、已知，若函数与函数的图象如下图，

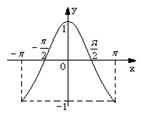
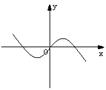
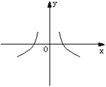
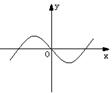则函数的图象可能是下图中的（　　）

　

　　　　　　　　　　　　　　　　　　　　　

（A）　　　　　 （B）　　　　　 （C）　　　　  （D）

6、已知函数，

那么　　　　　　

7、已知函数在上是的减函数，则的取值范围是（　 ）

（A）　　（B） 　　（C） 　　（D）

8、若函数图象的对称轴方程是，则的取值是　　　　 。

9、关于函数，有下列命题：

①由，可得必是的整数倍；

②的表达式可改写为；

③的图象关于点对称；

④的图象关于直线对称。其中正确的序号是　　　　  。

10、已知不等式恒成立，求的取值范围。

11、已知函数，当时，恒成立，求实数的范围。

12、周总长14.8m的钢条制作一个长方体容器的框架，如果所制作容器的底面的一边比短边长0.5m。那么高为多少时容器的容器最大？并求出它的最大容积？

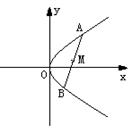13、定长为3的线段AB的两个端点在抛物线上移动，M为线段AB的中点。求M点到轴的最短距离。

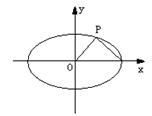14、已知椭圆，与轴正向交于点A，若这个椭圆上总存在点P，使得（O为原点），求离心率的取值范围。

15、已知二次函数（其中）的图象与轴有两个不同的公共点，若，且时，；

（1）求证：；　　　　（2）求证：

（3）求证：当，时，有