湖南省2006届高三 百校大联考 第一次考试

数 学 (理) 试 卷

总分：150分　　时量：120分钟　 2006年3月12日

第Ⅰ卷（选择题）

一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的．

1、　　已知那么复数z对应的点位于复平面内的（　　）

　 A、第一象限　　　　　B、第二象限　　　　 C、第三象限　　　　D、第四象限

2、　  过点作圆的两切线，设两切点为、，圆心为，则过、、的圆方程是　　　　　  （　 ）

A、　　 　　　　　　　　 B、　　　 C、　　　　　　　　　　　　　　 D、

3、　  已知椭圆与双曲线有相同的准线，则动点的轨迹为（　 ）

A、椭圆的一部分　　　　　　　　　　　　　　 B、双曲线的一部分　　C、抛物线的一部分　　　　　　　　　　　　　　  D、直线的一部分

4、　  若圆x²+y²=r²(r>0)至少能盖住函数的一个最大值点和一个最小值点，则r的取值范围是（　　 ）　　　　　　　　　　

A、　　B、　 C、　　 D、以上都不对

5、　  已知(3x+2)ⁿ(n∈N^*)的展开式中各项的二次项系数和为S_n，各项系数和为T_n, 则的值为　　　　　　　　　　　　　　　　（　　）

A、　１　　　B、　０　　　　　C、　　　　　　D、－１

6、　　若a、b为正实数，则R、S、T的大小关系为 （　　 ）

A、T≥R≥S　　B、R≥T≥S　　C、S≥T≥R　　 D、T≥S≥R

7、　　已知函数的定义域为R，它的反函数为，如果与互为反函数且　（为非零常数）则的值为 （　）

A、　　　　　　B、　0　　　　　　 C、　　　　　　　　D、　

8、　  一条长椅上有9个座位，若3个人坐，要求相邻2人之间至少有2个空椅子，则共有（　　　 ）种不同的坐法。

A、84　　　 B、72　　　 C、60　　　　 D、48

9、　  已知A、B、C三点共线，O是这条直线外一点，设且存在实数m，使成立，则点A分的比为（　　）

A 、　　  B、 　　　C、 　　　 D 、　 

10、　　　　　　  已知都是定义在R上的函数, g(x)≠0,,，，在有穷数列{}( n=1,2,…,10）中，任意取前k项相加，则前k项和大于的概率是（　 ）

A、　　　　　　  B、　　　　　　　 C、　　　　　  　D、

二、填空题（每题4分，共20分）

11、　　　　　　  　　　　　　。

12、　　　　　　  已知球的内接正方体的棱长为2，则该球的体积为　　　　．

13、　　　　　　  已知数列满足：，，则等于______

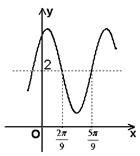
14、　　　　　　  函数

的图象如右，则=______,=______.

15、　　　　　　  给出如下4个命题：①若α、β是两个不重合的平面，、m是两条不重合的直线，则α∥β的一个充分而不必要条件是⊥α，m⊥β，且∥m；②对于任意一条直线a，平面α内必有无数条直线与a垂直；③已知命题P：若四点不共面，那么这四点中任何三点都不共线.而命题P的逆否命题是假命题；④已知a、b、c、d是四条不重合的直线，如果a⊥c，a⊥d，b⊥c，b⊥d，则“a∥b”与“c∥d”不可能都不成立.在以上4个命题中，正确命题的序号是______. (要求将所有你认为正确的命题序号都填上)　

湖南省2006届高三百校大联考第一次考试

数学答卷（理科）

					一 、选择题： 序号 1 2 3 4 5 6 7 8 9 10 答案 二、填空题： 11__________12__________13__________14__________15___________ 三、解答题： 16、（本小题12分）设 ，试求的值

座位号

17、　　（本小题满分14分）甲、乙两名射击运动员，甲射击一次命中10环的概率为，乙射击一次命中10环的概率为s，若他们各自独立地射击两次，设乙命中10环的次数为ξ，且ξ的数学期望Eξ=，表示甲与乙命中10环的次数的差的绝对值. 　　(1)求s的值及的分布列， 　　(2)求的数学期望.

18、(本小题满分12分) （本小题满分12分）如图，已知ABCD是正方形，PD⊥平面ABCD，PD=AD. 　　(1)求二面角A-PB-D的大小, 　　(2)在线段PB上是否存在一点E,使PC⊥平面ADE?若存在,确定E点的位置,若不存在,说明理由.

座位号

21、　　（本小题满分14分）已知曲线C为顶点在原点，以x轴为对称轴，开口向右的抛物线，又点M（2，1）到抛物线C的准线的距离为， （1）求抛物线C的方程； （2）证明：过点M的任意一条直线与抛物线恒有公共点； （3）若（2）中的直线（i=1，2，3，4）分别与抛物线C交于上下两点，又点的纵坐标依次成公差不为0的等差数列，试分析的大小关系。

湖南省2006届高三百校大联考第一次考试

数学（理科）答案

一、CADBD、ADCAC

二、11、　 12、 　 13、　　14、3，　 15、①②④

三、

17、解:(1)依题意知ξ∽B(2，s)，故Eξ=2s=，

　 ∴s=．　　　　　　　　　　　　　　　　　　　 …………2分

　 的取值可以是0，1，2.

甲、乙两人命中10环的次数均为0次的概率是，

甲、乙两人命中10环的次数均为1次的概率是，

甲、乙两人命中10环的次数均为2次的概率是，

∴(=0)=．　　　　　　　　  …………6分

甲命中10环的次数为2次且乙命中10环的次数为0次的概率是，

甲命中10环的次数为0次且乙命中10环的次数为2次的概率是．

∴(=2)==，　　　　　　　　　　　　　　 

∴(=1)=1(=0)(=2)=．　………10分

故的分布列是

	0	1	2

………12分

（2）E=．　　　　　　 …………14分

18、 (1)解法一:联结AC交DB于点O.　　　 ∵ABCD是正方形,∴AC⊥DB.

又PD⊥平面ABCD,AC平面ABCD,　　　 ∴AC⊥PD, ∴AC⊥平面PBD.

作OF⊥PB于点F,联结AF,则AF⊥PB. ∴∠OFA就是二面角A-PB-D的平面角. …………2分

∵PD⊥平面ABCD，AB⊥AD，∴PA⊥AB. 令PD=AD=2，则在RTABC中,PA=,AB=2.

　　　 ∴PB=,∴.

　　　 ∴在RTAOF中,sin,∴.

　　　 ∴二面角A-PB-D的大小为.　…6分

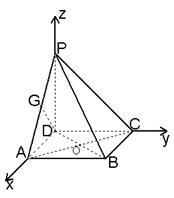
　　　  解法二:建立如图所示的直角坐标系.

　　 　联结AC,交BD于点O,取PA中点G,联结DG.

∵ABCD是正方形,∴AC⊥DB.

　　　 又PD⊥平面ABCD,AC平面ABCD,

　　　 ∴AC⊥PD, ∴AC⊥平面PBD.

　　　 ∵PD⊥平面ABCD，AB⊥AD，∴PA⊥AB.

　　　 ∴AB⊥平面PAD.

　　　 ∵PD=AD,G为PA中点, ∴GD⊥平面PAB.

　　　 故向量分别是平面PBD与平面PAB的法向量.

　　　 令PD=AD=2，则A(2，0，0)，C(0，2，0)，∴=(-2，2，0).

　　　 ∵P(0,0,2),A(2,0,0), ∴G(1,0,1),∴=(1,0,1). ………4分

∴向量的夹角余弦为，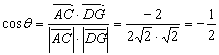

∴,∴二面角A-PB-D的大小为.　 …6分

(2)解法一: 当点E是线段PB中点时,

有PC⊥平面ADE.　　　 …………7分

证明如下:

　　　 取PC中点H,联结EH,DH,则有EH∥BC,

又BC∥AD,故有EH∥AD.　　 ∴平面ADE即平面ADHE.　　　　　　 …………9分

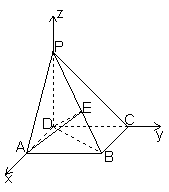　　 ∵PD=DC,H为PC中点, ∴PC⊥DH.又∵PD⊥平面ABCD，AD⊥CD，∴AD⊥PC.

∴PC⊥平面ADHE,即PC⊥平面ADE.　　　　………12分

解法二：建立如图所示的直角坐标系.

　　 ∵PD⊥平面ABCD，AD⊥CD，∴AD⊥PC.

　设E是线段PB上的一点，令.

　　 令PD=AD=2，则P(0,0,2),A(2,0,0),B(2,2,0),C(0,2,0),

 ∴(-2,0,2),(2,2,-2),(0,2,-2).

∴. ∴.…10分

令2(-)=0,得.

∴当,即点E是线段PB中点时,有AE⊥PC.又∵PD⊥平面ABCD，AD⊥CD，∴AD⊥PC.∴当点E是线段PB中点时,有PC⊥平面ADE.　　…12分

19、解：∵，

∴．　　　 …………2分

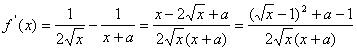∴．…4分

当(0，1]时,由于,故>0．

(1)当≥1时

≥0在区间(0，1]上恒成立，　∴在区间(0，1]上是增函数．

　　∴在区间(0，1]上的最大值是．　………8分

　　(2)当0<<1时＞0 ．　　＜0．

　　由于＜１，＞１，

故函数在区间(0，]上是增函数，在区间（，１］上是减函数．　　　　　　　　　　　 

∴在区间(0，1]上的最大值是（）＝．…………14分

20、解：

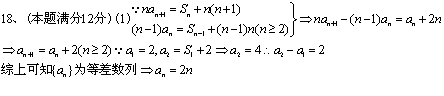
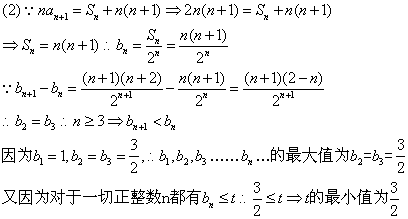
21、解：（1）依题设抛物线C的方程为：

由条件可知曲线C的方程为

（2）由题设，过M的l­_­i的方程为x-2+t(y-1)=0,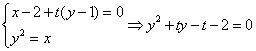

△=t²+4t+8>0,对于一切t成立，∴过点M的任意一条直线l_i与C恒有公共点。

(3)设，由定比分点坐标公式得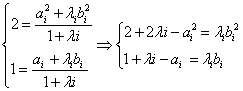：，消去b_i得