高三数学精品复习试卷(1)——集合
(时间:120分钟 满分:150分)
一、 选择题(每小题5分,共12题)
1.
若集合M={xx≥![]() },m=
},m=![]() ,则下列各式中正确的是( )
,则下列各式中正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知集合M={xx=3m+1,m![]() Z},N={yy=3n+2, n
Z},N={yy=3n+2, n![]() Z},若x0
Z},若x0![]() M,y0
M,y0![]() N,则x0y0与集合M,N的关系是( )
N,则x0y0与集合M,N的关系是( )
A.x0y0![]() M但
M但![]() N
B.x0y0
N
B.x0y0
![]() N但
N但![]() M
M
C.x0y0![]() M且
M且![]() N
D.x0y0
N
D.x0y0![]() M且
M且![]() N
N
3.已知全集U={1,2,3,4,5,6,7},M={3,4,5},N={1,3,6},则集合{2,7}=( )
A.M![]() N
B.
N
B.![]()
C.![]() D.M
D.M![]() N
N
4.关于x的不等式x-1>m的解集为R的充要条件是( )
A.m<0 B.m≤-1 C.m≤0 D.m≤1
5.集合M={ mm=2a-1,a![]() Z }与N={ nn=4b
Z }与N={ nn=4b![]() 1,b
1,b![]() Z }之间的关系是( )
Z }之间的关系是( )
A. M![]() N
B.M
N
B.M![]() N
N
C. M= N
D.M![]()
6.已知集合A={ yy=![]() ,x>1`},B={ yy=
,x>1`},B={ yy=![]() , x>1 },则A
, x>1 },则A![]() B等于( )
B等于( )
A.{y0<y<![]() } B.{yy>0} C.
} B.{yy>0} C. ![]() D.R
D.R
7.不等式x(1-2x) >0的解集是( )
A.![]() B.
B.![]()
C. ![]() D.
D. ![]()
8.设p、q为简单命题,则“p且q”为假是“p或q”为假的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
9.如果命题“![]() ”为假命题,则( )
”为假命题,则( )
A.p、q均为真命题 B.p、q均为假命题
C.p、q中至少有一个为真命题 D.p、q中至多有一个为真命题
10.条件p:x+1>2,条件:![]() ,则
,则![]() 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C充要条件 D.既不充分又不必要条件
11.已知集合M={![]() },N={
},N={![]() },P={
},P={![]() },则下列关系式中成立的是( )
},则下列关系式中成立的是( )
A.P![]() N
N![]() M
B.P=N
M
B.P=N![]() M
M
C. P![]() N=M.
D.P=N=M
N=M.
D.P=N=M
12.已知集合![]() ,,若M
,,若M![]() N=N,则实数的值是( )
N=N,则实数的值是( )
A.1 B.-1
C.1或-1 D.0、1或-1
二、 填空题(每小题4分,共16分)
13.满足集合A![]() B={1,2}的A、B的对数有_____对。
B={1,2}的A、B的对数有_____对。
14.设A={![]() },用列举法表示A为_____。
},用列举法表示A为_____。
15.已知集合M={![]() },集合P={
},集合P={![]() },则M
},则M![]() P=
P=![]() 的充要条件是_____。
的充要条件是_____。
16.有系列四个命题:
①命题“若xy=1”, 则“x,y互为倒数”的逆命题;
②命题“面积相等的三角形全等”的否命题;
③④命题“若![]() 有实根”的逆否命题;
有实根”的逆否命题;
命题“若![]() ,则
,则![]() ”的逆否命题。
”的逆否命题。
其中是真命题的是________(填上你认为正确的命题的序号)。
三、 解答题(本大题共6小题,共74分)
17.(12分)用反证法证明:若![]() ,且
,且![]() ,则x、y、z中至少有一个不小于0。
,则x、y、z中至少有一个不小于0。
18.(14分)某校高中部先后举行了数理化三科竞赛,学生中至少参加一科竞赛的有:数学807人,物理739人,化学437人,至少参加其中两科的有:数学与化学371人,物理与化学267人,三科都参加的有213人,试计算参加竞赛的学生总数。
19.(12分)设集合A=![]() ,B=
,B=![]() ,若A
,若A![]() B=
B=![]() ,求实数a的取值范围。
,求实数a的取值范围。
20.(12分)已知a<1,解关于x的不等式![]() 。
。
21.(12分)已知关于x的不等式![]() 的解集为M。
的解集为M。
①当a=4时,求集合M;
②当3![]() 且5
且5![]() ,求实数a的取值范围。
,求实数a的取值范围。
22.(12分)给出下列两个命题:
P:函数![]() 在定义域上单调递增
在定义域上单调递增
Q:不等式![]() 的解集为
的解集为![]() ,若P、Q有且只有一个正确,求实数a的取值范围。
,若P、Q有且只有一个正确,求实数a的取值范围。
参考答案
一、 选择题:1.D 2 .B. 3.B 4.A 5.C 6.B 7.B 8.B 9.C 10.A 11.A 12.D
二、 填空题:13、9 14、![]() 15、
15、![]() 或
或![]() 16、①、②、③
16、①、②、③
三、 解答题
17.(本题12分)
证明: 假设![]() 、
、![]() 、
、![]() 均小于0,即:
均小于0,即:
![]()
![]() ----① ;
----① ;
![]() ----② ;
----② ;
![]() ----③;
----③;
①+②+③相加得![]() ,
,
这与![]() 矛盾,
矛盾,
则假设不成立,∴![]() 、
、![]() 、
、![]() 中至少有一个不小于0。
中至少有一个不小于0。
18.解:由公式或如图填数字计算
Card(A![]() B
B![]() C)= Card(A)+ Card(B)+ Card(C)- Card(A
C)= Card(A)+ Card(B)+ Card(C)- Card(A![]() B) - Card(A
B) - Card(A![]() C) - Card(C
C) - Card(C![]() B)+ Card(A
B)+ Card(A![]() B
B![]() C)
C)
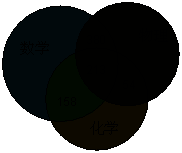 19.解:
19.解:![]()
![]()
![]()
![]() ,
, ![]()
实数a的取值范围是:![]()
20.解:不等式![]() 可化为
可化为![]() .
.
∵![]() ,∴
,∴![]() ,故原不等式可化为
,故原不等式可化为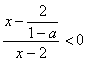 ,
,
故当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]()
故当![]() 时,原不等式的解集为
时,原不等式的解集为![]() .
.
21.解:(Ⅰ)当a = 4时,原不等式可以化为![]() ,即
,即![]()
![]() 故 M为
故 M为![]()
(Ⅱ)由3∈M得:![]() ①,且
①,且![]() ② 由①②得:
② 由①②得:![]()
22.解:依题意,P正确的a的取值范围为0<a<1.
Q成立即a=2或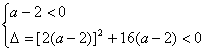
解得![]() .
.
∴P正确且Q不正确的a的取值范围为![]() ; P正确且Q正确的a的取值范围为
; P正确且Q正确的a的取值范围为![]() ; P、Q有且只有一个正确的a的取值范围为
; P、Q有且只有一个正确的a的取值范围为![]() .
.