数列部分

选择题

1. （广东卷）已知数列满足，，…．若，则(B)

（Ａ）（Ｂ）３（Ｃ）４（Ｄ）５

2. （福建卷）3．已知等差数列中，的值是　　　　　　　　　（ A　 ）

　　　 A．15　　　　　　　　　　　B．30　　　　　　　　　　　 C．31　　　　　　　　　　　D．64

3. （湖南卷）已知数列满足，则=　　　　 （B ）

　　　 A．0　　　　　　　　　　　　B．　　　　　　　　 C．　　　　　　　　　　D．

4. （湖南卷）已知数列{log₂(a_n－1)}（n∈N^*）为等差数列，且a₁＝3，a₂＝5，则

　　=　　　　　　　　　　　　　　　　　　　　　　　　　　　（C）

　　A．2　　　　　　　　　　 B．　　　　　　　　　 C．1　　　　　　　　　　 D．

5. （湖南卷）设f₀(x)＝sinx，f₁(x)＝f₀′(x)，f₂(x)＝f₁′(x)，…，f_n＋1(x)＝f_n′(x)，n∈N，则f₂₀₀₅(x)＝（C）

　　A．sinx　　　　　　　　　 B．－sinx　　　　　　　　C．cosx　　　　　　　　　D．－cosx

6. （江苏卷）在各项都为正数的等比数列｛a_n｝中，首项a₁=3 ，前三项和为21，则a₃+ a₄+ a₅=(C )

　　( A )　33　　　　 ( B ) 72　　　　  ( C )　84　　　　 ( D )189

7. (全国卷II) 如果数列是等差数列，则(B )

(A)　　　(B) 　　(C) 　　(D)

8. (全国卷II) 11如果为各项都大于零的等差数列，公差，则(B)

(A)　　　　　　 (B) 　　　　　 (C) 　　(D)

9. （山东卷）是首项=1，公差为=3的等差数列，如果=2005，则序号等于(C )

（A）667　　　　　　　　 （B）668　　　　  （C）669　　　 （D）670

10. （上海）16．用n个不同的实数a₁,a₂,┄a_n可得n!个不同的排列,每个排列为一行写成　　 1　2  3

一个n!行的数阵.对第i行a_i1,a_i2,┄a_in,记b_i=- a_i1+2a_i2-3 a_i3+┄+(-1)ⁿna_in,　　　 1　3  2

i=1,2,3, ┄,n!.用1,2,3可你数阵如右,由于此数阵中每一列各数之和都　　　  2　1　3

是12,所以,b₁+b₂+┄+b₆=-12+212-312=-24.那么,在用1,2,3,4,5形成　　 2　3　1

的数阵中, b₁+b₂+┄+b₁₂₀等于　　　　　　　　　　　　　　　　　　　　  3  1　2

3　　　　 2　1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 [答]( C　　)

　  (A)-3600　　　 (B) 1800　　　 (C)-1080　　　  (D)-720

11. （浙江卷）＝( C　 )

(A) 2　　 (B) 4　　 (C) 　　　 (D)0

12. (重庆卷) 有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2，且改塔形的表面积(含最底层正方体的底面面积)超过39，则该塔形中正方体的个数至少是( C)

　　(A) 4；

　　(B) 5；

　　(C) 6；

　　(D) 7。

13. （江西卷）

填空题

1. （广东卷）

设平面内有ｎ条直线，其中有且仅有两条直线互相平行，任意三角形不过同一点．若用表示这ｎ条直线交点的个数，则_____5________；当ｎ＞４时，＝_____________．

2. （北京卷）已知n次多项式,

　  如果在一种算法中，计算（k＝2，3，4，…，n）的值需要k－1次乘法，计算的值共需要9次运算（6次乘法，3次加法），那么计算的值共需要 n(n＋3)　　　　　　  次运算．

　  下面给出一种减少运算次数的算法：（k＝0， 1，2，…，n－1）．利用该算法，计算的值共需要6次运算，计算的

值共需要　　 2n　　次运算．

3. （湖北卷）设等比数列的公比为q，前n项和为S­_n，若S_n+1,S­_n，S_n+2成等差数列，则q的值为 　　-2　　　　  .

4. (全国卷II) 在和之间插入三个数，使这五个数成等比数列，则插入的三个数的乘积为_______216 __．

5. （山东卷）

6. （上海）12、用个不同的实数可得到个不同的排列，每个排列为一行写成一个行的数阵。对第行，记，。例如：用1，2，3可得数阵如图，由于此数阵中每一列各数之和都是12，所以，，那么，在用1，2，3，4，5形成的数阵中，=_-1080_________。

7、计算：=_3 _________。

8. （天津卷）设,则

9. （天津卷）在数列{a_n}中, a₁=1, a₂=2,且，

则=_2600_　　　　___.

10. (重庆卷)= -3　　　　　　  .

解答题

1.（北京卷）

设数列{a_n}的首项a₁=a≠，且,

记，n＝＝l，2，3，…·．

（I）求a₂，a₃；

（II）判断数列{b_n}是否为等比数列，并证明你的结论；

（III）求．

解：（I）a₂＝a₁+=a+，a₃=a₂=a+；

（II）∵ a₄=a₃+=a+, 所以a₅=a₄=a+,

所以b₁=a₁－=a－, b₂=a₃－=(a－), b₃=a₅－=(a－),

猜想：{b_n}是公比为的等比数列·

　  证明如下：

　  因为b_n+1＝a_2n+1－=a_2n－=(a_2n－1－)=b_n, (n∈N*)

　  所以{b_n}是首项为a－, 公比为的等比数列·

　  （III）.

2.（北京卷）数列{a_n}的前n项和为S_n，且a₁=1，，n=1，2，3，……，求

　 （I）a₂，a₃，a₄的值及数列{a_n}的通项公式；

　 （II）的值.

解：（I）由a₁=1，，n=1，2，3，……，得

，，，

由（n≥2），得（n≥2），

又a₂=，所以a_n=(n≥2),

∴ 数列{a_n}的通项公式为；

（II）由（I）可知是首项为，公比为项数为n的等比数列，∴ =

3．（福建卷）

　　　 已知{}是公比为q的等比数列，且成等差数列.

　 （Ⅰ）求q的值；

（Ⅱ）设{}是以2为首项，q为公差的等差数列，其前n项和为S_n，当n≥2时，比较S_n与b_n的大小，并说明理由.

解：（Ⅰ）由题设　

（Ⅱ）若

当　故

若

当

故对于

4. （福建卷）已知数列{a_n}满足a₁=a, a_n+1=1+我们知道当a取不同的值时，得到不同的数列，如当a=1时，得到无穷数列：

（Ⅰ）求当a为何值时a₄=0；

（Ⅱ）设数列{b_n­}满足b₁=－1, b_n+1=，求证a取数列{b_n}中的任一个数，都可以得到一个有穷数列{a_n}；

（Ⅲ）若，求a的取值范围.

　 （I）解法一：

　　　　

故a取数列{b_n}中的任一个数，都可以得到一个有穷数列{a_n}

5. （湖北卷）设数列的前n项和为S_n=2n²，为等比数列，且

　 （Ⅰ）求数列和的通项公式；

　 （Ⅱ）设，求数列的前n项和T_n.

解：（1）：当

故{a_n}的通项公式为的等差数列.

设{b_n}的通项公式为

故

（II）

两式相减得

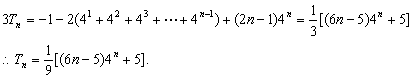
6. （湖北卷）已知不等式为大于2的整数，表示不超过的最大整数. 设数列的各项为正，且满足

　 （Ⅰ）证明

（Ⅱ）猜测数列是否有极限？如果有，写出极限的值（不必证明）；

（Ⅲ）试确定一个正整数N，使得当时，对任意b>0，都有

解：（Ⅰ）证法1：∵当

即　

于是有　

所有不等式两边相加可得　

由已知不等式知，当n≥3时有，

∵

证法2：设，首先利用数学归纳法证不等式

　 （i）当n=3时，　由

知不等式成立.

（ii）假设当n=k（k≥3）时，不等式成立，即

则

即当n=k+1时，不等式也成立.

由（i）、（ii）知，

又由已知不等式得　

　 （Ⅱ）有极限，且

　 （Ⅲ）∵

则有

故取N=1024，可使当n>N时，都有

7. （湖南卷）已知数列为等差数列，且

　 （Ⅰ）求数列的通项公式；

　 （Ⅱ）证明

（I）解：设等差数列的公差为d.

　　由即d=1.

所以即

（II）证明因为，

所以

　

8. （湖南卷）自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用x_n表示某鱼群在第n年年初的总量，n∈N^*，且x₁＞0.不考虑其它因素，设在第n年内鱼群的繁殖量及捕捞量都与x_n成正比，死亡量与x_n²成正比，这些比例系数依次为正常数a，b，c.

　 （Ⅰ）求x_n+1与x_n的关系式；

　 （Ⅱ）猜测：当且仅当x₁，a，b，c满足什么条件时，每年年初鱼群的总量保持不变？（不

要求证明）

　 （Ⅱ）设a＝2，b＝1，为保证对任意x₁∈（0,2），都有x_n＞0，n∈N^*，则捕捞强度b的

　　　　 最大允许值是多少？证明你的结论.

解（I）从第n年初到第n+1年初，鱼群的繁殖量为ax_n，被捕捞量为bx_n，死亡量为

　 （II）若每年年初鱼群总量保持不变，则x_n恒等于x₁， n∈N*，从而由（*）式得

　　　　

　　　　因为x₁>0，所以a>b.

　　　　猜测：当且仅当a>b，且时，每年年初鱼群的总量保持不变.

　 （Ⅲ）若b的值使得x_n>0，n∈N*

　　　　 由x_n+1=x_n(3－b－x_n), n∈N*, 知

　　　　 0<x_n<3－b, n∈N*, 特别地，有0<x₁<3－b. 即0<b<3－x₁.

　　　　而x₁∈(0, 2)，所以

　　　　由此猜测b的最大允许值是1.

　　　　下证 当x₁∈(0, 2) ，b=1时，都有x_n∈(0, 2), n∈N*

　　　　①当n=1时，结论显然成立.

②假设当n=k时结论成立，即x_k∈(0, 2),

则当n=k+1时，x_k+1=x_k(2－x_k­)>0.

又因为x_k+1=x_k(2－x_k)=－(x_k－1)²+1≤1<2,

所以x_k+1∈(0, 2)，故当n=k+1时结论也成立.

由①、②可知，对于任意的n∈N*，都有x_n∈(0,2).

综上所述，为保证对任意x₁∈(0, 2), 都有x_n>0， n∈N*，则捕捞强度b的最大允许值是1.

9. （江苏卷）设数列｛a_n｝的前项和为,已知a₁=1, a₂=6, a₃=11,且, 其中A,B为常数.

(Ⅰ)求A与B的值;

(Ⅱ)证明数列｛a_n｝为等差数列;

(Ⅲ)证明不等式.

解：(Ⅰ)由，，，得，，．

把分别代入，得

解得，，．

(Ⅱ)由(Ⅰ)知，，即

，　　　　　　　　　　　①

又．　②

②-①得，，

即．　　　　　　　　 ③

又．　　　　　　　　④

④-③得，，

∴，

∴，又，

因此，数列是首项为1，公差为5的等差数列．

(Ⅲ)由(Ⅱ)知，．考虑

．

．

∴．

即，∴．

因此，．

10. （辽宁卷）已知函数设数列}满足，数列}满足

　 （Ⅰ）用数学归纳法证明；

　 （Ⅱ）证明

解：（Ⅰ）证明：当　因为a₁=1，

所以 ………………2分

下面用数学归纳法证明不等式

　 （1）当n=1时，b₁=，不等式成立，

　 （2）假设当n=k时，不等式成立，即

那么　　 ………………6分

　　

所以，当n=k+1时，不等也成立。

根据（1）和（2），可知不等式对任意n∈N*都成立。　…………8分

（Ⅱ）证明：由（Ⅰ）知，

所以　

…………10分　

故对任意………………（12分）

11. (全国卷Ⅰ) 设正项等比数列的首项，前n项和为，且。

（Ⅰ）求的通项；

（Ⅱ）求的前n项和。

解：（Ⅰ）由  得

即

可得

因为，所以 　解得，因而

 （Ⅱ）因为是首项、公比的等比数列，故

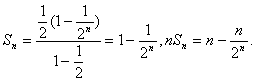
则数列的前n项和

前两式相减，得　

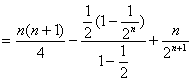　 即　

12. (全国卷Ⅰ)

设等比数列的公比为，前n项和。

（Ⅰ）求的取值范围；

（Ⅱ）设，记的前n项和为，试比较与的大小。

解：（Ⅰ）因为是等比数列，

当

上式等价于不等式组：　　  ①

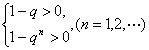或　 ②

解①式得q>1；解②，由于n可为奇数、可为偶数，得－1<q<1.

综上，q的取值范围是

（Ⅱ）由得

于是

又∵>0且－1<<0或>0

当或时即

当且≠0时，即

当或=2时，即

13. (全国卷II) 已知是各项为不同的正数的等差数列，、、成等差数列．又，．

(Ⅰ) 证明为等比数列；

(Ⅱ) 如果数列前3项的和等于，求数列的首项和公差．

 (I)证明：∵、、成等差数列

∴2=+，即

又设等差数列的公差为，则(－)=(－3)

这样，从而(－)=0

∵≠0

∴=≠0

∴

∴是首项为=，公比为的等比数列。

(II)解。∵

∴=3

∴==3

14.(全国卷II)

已知是各项为不同的正数的等差数列，、、成等差数列．又，．

(Ⅰ) 证明为等比数列；

(Ⅱ) 如果无穷等比数列各项的和，求数列的首项和公差．

(注：无穷数列各项的和即当时数列前项和的极限)

解：（Ⅰ）设数列{a_n}的公差为d，依题意，由  得

　　　即，得 　因

　当=0时，{a_n}为正的常数列 就有

　　当=时，,就有

于是数列{}是公比为1或的等比数列

（Ⅱ）如果无穷等比数列的公比=1，则当→∞时其前项和的极限不存在。

因而=≠0，这时公比=，

这样的前项和为

则S=

　　由，得公差=3，首项==3

15. (全国卷III)

在等差数列中，公差的等差中项.

已知数列成等比数列，求数列的通项

解：由题意得：……………1分　

　　　 即…………3分

又…………4分　

又成等比数列,

∴该数列的公比为，………6分

所以………8分

又……………………………………10分

所以数列的通项为……………………………12分

16. （山东卷）

已知数列的首项前项和为，且

（I）证明数列是等比数列；

（II）令，求函数在点处的导数并比较与的大小.

解：由已知可得两式相减得

即从而当时所以又所以从而

故总有，又从而即数列是等比数列；

（II）由（I）知

因为所以

从而=

=-=

由上-=

=12①

当时，①式=0所以；

当时，①式=-12所以

当时，又

所以即①从而

17．(上海)本题共有2个小题,第1小题满分6分, 第2小题满分8分.

假设某市2004年新建住房400万平方米,其中有250万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,

(1)该市历年所建中低价房的累计面积(以2004年为累计的第一年)将首次不少于4750万平方米?

(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?

 [解](1)设中低价房面积形成数列{a_n},由题意可知{a_n}是等差数列,

　 其中a₁=250,d=50,则S_n=250n+=25n²+225n,

　 令25n²+225n≥4750,即n²+9n-190≥0,而n是正整数, ∴n≥10.

到2013年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米.

(2)设新建住房面积形成数列{b_n},由题意可知{b_n}是等比数列,

其中b₁=400,q=1.08,则b_n=400·(1.08)^n-1·0.85.

　 由题意可知a_n>0.85 b_n,有250+(n-1)·50>400·(1.08)^n-1·0.85.

　 由计箅器解得满足上述不等式的最小正整数n=6.

　 到2009年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.

18. （天津卷）

已知.

（Ⅰ）当时，求数列的前n项和；

（Ⅱ）求.

（18）解：（Ⅰ）当时，．这时数列的前项和

．　　　①

①式两边同乘以，得　　　　　②　

①式减去②式，得　　

若，

，

若，

（Ⅱ）由（Ⅰ），当时，，则．

当时，

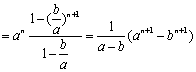
此时，．

若，．

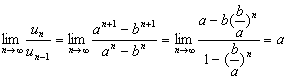若，．

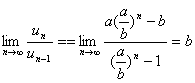19. （天津卷）若公比为c的等比数列｛｝的首项＝1且满足：（＝3，4，…）。

　　（I）求c的值。

（II）求数列｛｝的前项和。

20. （浙江卷）已知实数a，b，c成等差数列，a＋1，了＋1，c＋4成等比数列，求a，b，c．

解：由题意，得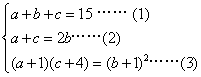　　　　 由(1)(2)两式，解得

将代入(3),整理得

解得 或

故,或

经验算，上述两组数符合题意。

21（浙江卷）设点(，0)，和抛物线：y＝x²＋a_n x＋b_n(n∈N*)，其中a_n＝－2－4n－，由以下方法得到：

　 x₁＝1，点P₂(x₂，2)在抛物线C₁：y＝x²＋a₁x＋b₁上，点A₁(x₁，0)到P₂的距离是A₁到C₁上点的最短距离，…，点在抛物线：y＝x²＋a_n x＋b_n上，点(，0)到的距离是 到 上点的最短距离．

　 (Ⅰ)求x₂及C₁的方程．

　 (Ⅱ)证明{}是等差数列．

解：（I）由题意，得。

设点是上任意一点，则

令 则

由题意，得即

又在上，

解得

故方程为

(II)设点是上任意一点，则

令，则.

由题意得g，即

又

即　 （*）

下面用数学归纳法证明

①当n=1时， 等式成立。

②假设当n=k时，等式成立，即

则当时，由（*）知

又

即当时，等式成立。

由①②知，等式对成立。

是等差数列。

22. (重庆卷)数列{a_n}满足a₁=1且8a_n+1-16a_n+1+2a_n+5=0 (n³1)。记(n³1)。

　　(1) 求b₁、b₂、b₃、b₄的值；

　　(2) 求数列{b_n}的通项公式及数列{a_nb_n}的前n项和S_n。

解法一：

（I）

（II）因，

故猜想

因，（否则将代入递推公式会导致矛盾）。

∵

故的等比数列.

, 　

解法二：

（Ⅰ）由

整理得

（Ⅱ）由

所以

故

由得

故

解法三：

（Ⅰ）同解法一

（Ⅱ）

　　　  

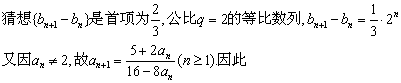
从而

故

23. (重庆卷)数列{a_n}满足.

（Ⅰ）用数学归纳法证明：；

（Ⅱ）已知不等式，其中无理数e=2.71828….

　 （Ⅰ）证明：（1）当n=2时，，不等式成立.

　 （2）假设当时不等式成立，即

那么.　这就是说，当时不等式成立.

根据（1）、（2）可知：成立.

（Ⅱ）证法一：

由递推公式及（Ⅰ）的结论有

两边取对数并利用已知不等式得

　故　

上式从1到求和可得

即

（Ⅱ）证法二：

由数学归纳法易证成立，故

令

取对数并利用已知不等式得　

上式从2到n求和得　

因

故成立

24. （江西卷）已知数列{a_n}的前n项和S_n满足S_n－S_n－2=3求数列{a_n}的通项公式.

解：方法一：先考虑偶数项有：

　　　 　　　　　　　　　　　　　 

　　　 　　　　　　　　　　　 　　　………

　　　 　　　　　　　　　　　　　 

　　　

　　　 同理考虑奇数项有：

………

　　　

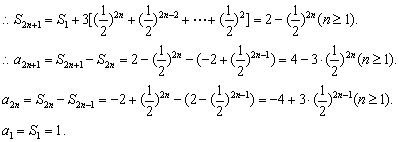
　　　 综合可得

　　　 方法二：因为

　　　 两边同乘以，可得：

令

所以

………

　

又

∴

∴

25. （江西卷）

已知数列

（1）证明

（2）求数列的通项公式a_n.

解：（1）方法一 用数学归纳法证明：

1°当n=1时，

　 ∴，命题正确.

2°假设n=k时有

　 则

　

而

又

∴时命题正确.

由1°、2°知，对一切n∈N时有

方法二：用数学归纳法证明：

　　　 1°当n=1时，∴；

　　2°假设n=k时有成立，

　　　 令，在[0，2]上单调递增，所以由假设

有：即

也即当n=k+1时　成立，所以对一切

　 （2）下面来求数列的通项：所以

,

又b_n=－1，所以