2006年普通高等学校招生全国统一考试数学分类汇编
第六章《不等式》
一、选择题（共15题）
1．（安徽卷）不等式
的解集是（ ）
A．
B．
C．
D．
解：由得：
，即
，故选D。
2．（江苏卷）设a、b、c是互不相等的正数，则下列等式中不恒成立的是
（A）
（B）
（C）
（D）
【思路点拨】本题主要考查.不等式恒成立的条件，由于给出的是不完全提干，必须结合选择支，才能得出正确的结论。
【正确解答】运用排除法，C选项
，当a-b<0时不成立。
【解后反思】运用公式一定要注意公式成立的条件
如果
如果a,b是正数，那么
3．（江西卷）若a>0，b>0，则不等式－b<
<a等价于（ ）
A．
<x<0或0<x<
B.－<x<
C.x<-或x> D.x<或x>
解：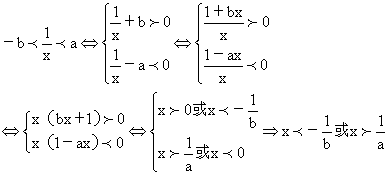
故选D
4．（山东卷）设f(x)=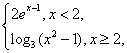 
则不等式f(x)>2的解集为
(A)（1，2）（3，+∞）
(B)（
，+∞）
(C)（1，2） （ ，+∞）
(D)（1，2）
解：令
>2（x<2），解得1<x<2。令
>2（x³2）解得xÎ（，+∞）选C
5．(陕西卷)已知不等式(x+y)( + )≥9对任意正实数x,y恒成立,则正实数a的最小值为( )
A.2 B.4 C.6 D.8
解析：不等式(x+y)(
)≥9对任意正实数x，y恒成立，则
≥
≥9，∴ 
≥2或≤－4(舍去)，所以正实数a的最小值为4，选B．
6．(陕西卷)已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2,x1+x2=1－a,则( )
A.f(x1)<f(x2) B.f(x1)=f(x2) C.f(x1)>f(x2) D.f(x1)与f(x2)的大小不能确定
解析：函数f(x)=ax2+2ax+4(0<a<3)，二次函数的图象开口向上，对称轴为
，0<a<3，∴ x1+x2=1－a∈(－2，1)，x1与x2的中点在(－1，
)之间，x1<x2，∴ x2到对称轴的距离大于x1到对称轴的距离，∴ f(x1)<f(x2)
，选A．
7．(陕西卷)已知函数f(x)=ax2+2ax+4(a>0),若x1<x2 , x1+x2=0 , 则( )
A.f(x1)<f(x2) B.f(x1)=f(x2) C.f(x1)>f(x2) D.f(x1)与f(x2)的大小不能确定
解析：函数f(x)=ax2+2ax+4(a>0)，二次函数的图象开口向上，对称轴为，a>0，∴ x1+x2=0，x1与x2的中点为0，x1<x2，∴ x2到对称轴的距离大于x1到对称轴的距离，∴ f(x1)<f(x2)
，选A．
8．(陕西卷)设x,y为正数, 则(x+y)( + )的最小值为( )
A. 6 B.9 C.12 D.15
解析：x，y为正数，(x+y)(
)≥
≥9，选B.
9．(上海卷)若关于
的不等式
≤
＋4的解集是M，则对任意实常数
，总有（ ）
（A）2∈M，0∈M； （B）2
M，0M； （C）2∈M，0M； （D）2M，0∈M．
解：选（A）
方法1：代入判断法，将
分别代入不等式中，判断关于
的不等式解集是否为
；
方法2：求出不等式的解集：≤＋4
；
10．(上海卷)如果
，那么，下列不等式中正确的是（ ）
（A）
（B）
（C）
（D）
解：如果，那么
，∴ ，选A.
11．（浙江卷）“a＞b＞c”是“ab＜
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不允分也不必要条件
【考点分析】本题考查平方不等式和充要条件，基础题。
解析：由
能推出
；但反之不然，因此平方不等式的条件是
。
12．（浙江卷）“a＞0，b＞0”是“ab>0”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不允分也不必要条件
解：由“a＞0，b＞0”可推出“ab>0”，反之不一定成立，选A
13．(重庆卷)若a,b,c＞0且a(a+b+c)+bc=4-2
,则2a+b+c的最小值为
（A）-1 (B) +1
(C) 2+2
(D) 2-2
解析：若
且
所以
，
∴ 
，则(
)≥
，选D.
14．(重庆卷)若且
，则
的最小值是
（A）
（B）3 （C）2 （D）
解：（a＋b＋c）2＝a2＋b2＋c2＋2ab＋2ac＋2bc＝12＋（b－c）2³12，当且仅当b＝c时取等号，故选A
15．（上海春）若
，则下列不等式成立的是( )
（A）
. （B）
. （C）
.（D）
.
解：应用间接排除法．取a=1,b=0，排除A. 取a=0,b=-1，排除B; 取c=0，排除D．故应该选C．显然 
，对不等式a>b的两边同时乘以 
，立得
成立．
二、填空题（共6题）
16．（江苏卷）不等式
的解集为
【思路点拨】本题考查对数函数单调性和不等式的解法
【正确解答】
，0〈
，
.
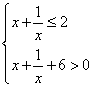解得
【解后反思】在数的比较大小过程中,要遵循这样的规律,异中求同即先将这些数的部分因式化成相同的部分,再去比较它们剩余部分,就会很轻易啦.一般在数的比较大小中有如下几种方法：(1)作差比较法和作商比较法,前者和零比较,后者和1比较大小；(2)找中间量,往往是1,在这些数中,有的比1大,有的比1小；,(3)计算所有数的值；(4)选用数形结合的方法,画出相应的图形；(5)利用函数的单调性等等.
17．(上海卷)三个同学对问题“关于的不等式
＋25＋
－5≥
在[1，12]上恒成立，求实数
的取值范围”提出各自的解题思路．
甲说：“只须不等式左边的最小值不小于右边的最大值”．
乙说：“把不等式变形为左边含变量的函数，右边仅含常数，求函数的最值”．
丙说：“把不等式两边看成关于的函数，作出函数图像”．
参考上述解题思路，你认为他们所讨论的问题的正确结论，即的取值范围是 ．
解：由＋25＋－5≥
，而
，等号当且仅当
时成立；且
，等号当且仅当时成立；所以，
，等号当且仅当
时成立；故
；
18．（天津卷）某公司一年购买某种货物400吨，每次都购买吨，运费为4万元/次，一年的总存储费用为
万元，要使一年的总运费与总存储费用之和最小，则
_______
吨．
解：某公司一年购买某种货物400吨，每次都购买吨，则需要购买
次，运费为4万元/次，一年的总存储费用为万元，一年的总运费与总存储费用之和为
万元，≥160，当
即20吨时，一年的总运费与总存储费用之和最小。
19.（浙江卷）不等式
的解集是 。.
解：Û（x＋1）（x－2）>0Ûx<－1或x>2.
20.（上海春）不等式
的解集是 .
解：应用结论： 
．不等式 
等价于(1-2x)(x+1)>0，也就是 
，所以 
，从而应填 
．
21.（上海春）已知直线
过点
，且与
轴、
轴的正半轴分别交于
两点，
为坐标原点，则三角形
面积的最小值为 .
解：设直线 l 为 
，则有关系
． 对 
应用２元均值不等式，得
，即ab≥8 ．于是，△OAB 面积为
．从而应填4．
三、解答题（共1题）
22.（湖南卷）对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为:
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为(1≤a≤3).设用单位质量的水初次清洗后的清洁度是
(
),用
质量的水第二次清洗后的清洁度是
,其中
是该物体初次清洗后的清洁度.
(Ⅰ)分别求出方案甲以及
时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论取不同数值时对最少总用水量多少的影响.
解：(Ⅰ)设方案甲与方案乙的用水量分别为x与z,由题设有=0.99,解得x=19.
由得方案乙初次用水量为3, 第二次用水量y满足方程:
解得y=4,故z=4
+3.即两种方案的用水量分别为19与4+3.
因为当
,故方案乙的用水量较少.
（II）设初次与第二次清洗的用水量分别为与，类似（I）得
，
（*）
于是
+
当为定值时,
,
当且仅当
时等号成立.此时
将
代入（*）式得
故时总用水量最少, 此时第一次与第二次用水量分别为 
, 最少总用水量是
.
当
,故T()是增函数(也可以用二次函数的单调性判断).这说明,随着的值的最少总用水量, 最少总用水量最少总用水量.