数学测试
2006.9
一.选择题
1.函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若条件P:![]() ,条件Q:
,条件Q:![]() ,则¬P是¬Q的( )条件.
,则¬P是¬Q的( )条件.
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
3.函数![]() 的图象大致是( )
的图象大致是( ) 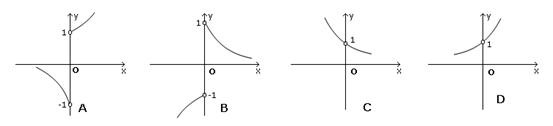
4.设![]() ,则
,则![]() =( )
=( )
A.1 B.0 C.![]() D.
D.![]()
5.(理)![]() ( )
( )
A.0 B.-1 C.1 D.![]()
(文)如果![]() 成等比数列,那么
成等比数列,那么
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设![]() 是
是![]() 的反函数,若
的反函数,若![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.1 B.2 C.![]() D.4
D.4
7.设M={1,2,3,4},N={0,1,2},建立![]() 的函数,则以N为值域的映射有( )
的函数,则以N为值域的映射有( )
A.18个 B.36个 C.48个 D.81个
8.下列条件中,能确定三点A,B,P不共线的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.(理)![]() (
(![]() )分别是定义在R上的奇函数和偶函数,当
)分别是定义在R上的奇函数和偶函数,当![]() 时,
时,![]() ,且
,且![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(文)曲线![]() 与
与![]() 在交点处的切线的夹角是( )
在交点处的切线的夹角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.己知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,点P在双曲线的右支上,若此双曲线的离心率为
,点P在双曲线的右支上,若此双曲线的离心率为![]() ,且
,且![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
11.设实数![]() 满足
满足![]() ,若对满足条件的
,若对满足条件的![]() ,不等式
,不等式![]() 恒成立,则c的取值范围是( )
恒成立,则c的取值范围是( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
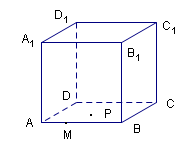
12.如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且AM=![]() ,点P是平面ABCD上的动点,且P点到直线A1D1的距离与点P到点M的距离的平方差为1,则动点P的轨迹是( )
,点P是平面ABCD上的动点,且P点到直线A1D1的距离与点P到点M的距离的平方差为1,则动点P的轨迹是( )
A.圆 B.抛物线
C.双曲线 D.直线
二.填空题
13.己知点P![]() ,Q
,Q![]() ,直线
,直线![]() 与线段PQ相交,则实数a的取值范围是
与线段PQ相交,则实数a的取值范围是
 14.己知数列
14.己知数列![]() 的前n项和为
的前n项和为![]() ,且向量
,且向量![]() 与
与![]() 共线,则数列
共线,则数列![]() 的前n项和
的前n项和![]() =
=
15.关于x的方程![]() 有实根,则实数m的取值范围是
有实根,则实数m的取值范围是
16.把49个数排成如图所示的数表,若表中每行7个数自左至右依次成等差数列,每列自上而下依次也成等差数列,且正中间的数![]() =1,则表中所有数的和为
=1,则表中所有数的和为
三.解答题
17.己知![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,
(1)若 ![]() ,求
,求![]() 的值
的值
(2)若![]() ,求
,求![]() 的值
的值
18.(文)有一批食品出厂前要进行五项指标抽检,如果有两项指标不合格,则这批产品不能出厂,己知每项抽检是相互独立的,且每项抽检不合格的概率都是![]() ,
,
(1)求这批食品不能出厂的概率;(保留三位有效数字)
(2)求直到五项指标全部检验完毕,才能确定该食品是否可以出厂的概率。
(理)袋中有红球3个,蓝球2个,黄球1个,任取一球确认颜色后放回袋中,最多可以取3次,但是若取到红球就不能再取了,
(1)求取出一次或二次的概率;
(2)假定每取一次可以得100元,求所得金额的期望;
(3)求恰好两次取到蓝球的概率。
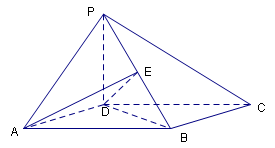 19.己知ABCD为矩形,PD
19.己知ABCD为矩形,PD![]() 平面ABCD,PD=DC=
平面ABCD,PD=DC=![]() ,AD=2,E为PB上一点,且PC
,AD=2,E为PB上一点,且PC![]() 平面ADE,
平面ADE,
(1)求PC与平面PBD所成角的大小;
(2)求![]() 的值
的值
(3)求四棱锥P-ABCD夹在平面ADE与底面ABCD之间部分的体积。
20.双曲线的中心是原点O,它的虚轴长为![]() ,相应于焦点F
,相应于焦点F![]() 的准线
的准线![]() 与x轴交于点A,且
与x轴交于点A,且![]() ,过点F的直线与双曲线交于P,Q两点,
,过点F的直线与双曲线交于P,Q两点,
(1)求双曲线方程及离心率;
(2)若![]() ,求直线PQ的方程。
,求直线PQ的方程。
21.(理)己知函数![]() ,
,![]() (
(![]() 为常数),直线
为常数),直线![]() 与函数
与函数![]() 及
及![]() 的图象都相切,且
的图象都相切,且![]() 与
与![]() 的切点的横坐标为1,
的切点的横坐标为1,
(1)求直线![]() 的方程及a的值;
的方程及a的值;
(2)当![]() 时,讨论方程
时,讨论方程![]() 的解的个数。
的解的个数。
(文)己知函数![]() 在区间(-2,1)内,当
在区间(-2,1)内,当![]() 时,取得极小值,
时,取得极小值,![]() 时,取得极大值,
时,取得极大值,
求(1)函数![]() 在
在![]() 时的对应点的切线方程;
时的对应点的切线方程;
(2)函数![]() 在
在![]() 上的最大值与最小值。
上的最大值与最小值。
22.设函数![]() 上两点P1
上两点P1![]() ,P2
,P2![]() ,若
,若![]() ,且P点的横坐标为
,且P点的横坐标为![]() ,
,
(1)求证:P点的纵坐标为定值1;
(2)求![]()
![]()
(3)记![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 对一切
对一切![]() 都成立,求实数a的取值范围。
都成立,求实数a的取值范围。
答案
一.选择
| 1 | 2 | 3 | 4 | 5 |
| C | A | B | D | D |
| 6 | 7 | 8 | 9 | 10 |
| D | B | C | A | D |
| 11 | 12 | |||
| A | B | |||
二.填空题
13.![]() 14.
14.![]() 15.[-3,0) 16.49
15.[-3,0) 16.49
三.解答题
17.(文/理)①![]()
②由![]() ,得
,得![]()
![]()
18.(理)①P1=![]()
|
| 100 | 200 | 300 |
| P |
|
|
|
②
![]() 元
元
③ P=![]()
(文)解:(1)![]()
(2)五项指标全部检验完毕,这批食品可以出厂的概率是![]()
五项指标全部检验完毕,这批食品不能出厂的概率是![]()
![]()
![]()
19.解:(1)在平面ABCD内作CG![]() BD于G,连结PG,
BD于G,连结PG,![]() PD
PD![]() 平面ABCD,CG
平面ABCD,CG![]() 平面ABCD,
平面ABCD,
![]() PD
PD![]() CG,
CG,![]() CG
CG![]() 平面PBD
平面PBD ![]()
![]() CPG就是PC与面PBD所成的角。
CPG就是PC与面PBD所成的角。
在![]() BCD中,CG=
BCD中,CG=![]() =
=![]() ,又PC=
,又PC=![]() ,故在
,故在![]() PGC中,
PGC中,![]() CPG=
CPG=![]()
又![]()
![]() CPG为锐角,
CPG为锐角,![]()
![]() CPG=
CPG=![]()
![]() PC与平面PBD所成的角为
PC与平面PBD所成的角为![]()
(2)设平面ADE与PC交于F,连DF,EF,![]() PC
PC![]() 平面ADE,DF
平面ADE,DF![]() 平面ADE,
平面ADE,![]() PC
PC![]() DF
DF
又![]() PD=DC,
PD=DC,![]() F为PC中点
F为PC中点 ![]() BC//AD,BC
BC//AD,BC![]() 平面ADE
平面ADE ![]() BC//平面ADE
BC//平面ADE
又平面ADE![]() 平面PBD=EF
平面PBD=EF ![]() BC//EF
BC//EF
![]() E为PB中点,故
E为PB中点,故![]()
(3)因为PD![]() 平面ABCD,所以PD
平面ABCD,所以PD![]() AD,又AD
AD,又AD![]() DC, 所以AD
DC, 所以AD![]() 平面PDC,又DF
平面PDC,又DF![]() 平面PDC,所以AD
平面PDC,所以AD![]() DF,又PF
DF,又PF![]() 平面ADEF,EF=
平面ADEF,EF=![]() BC=1,DF=
BC=1,DF=![]() DC=
DC=![]()
所以![]() ,又
,又![]()
所以![]() ,即四棱锥
,即四棱锥![]() 夹在平面ADE与底面ABCD之间部分的体积为5
夹在平面ADE与底面ABCD之间部分的体积为5
20.解:(Ⅰ)由题意,设曲线的方程为![]() = 1(a>0b>0)
= 1(a>0b>0)
由已知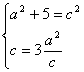 解得a =
解得a =![]() ,c = 3
,c = 3
所以双曲线的方程这![]() = 1离心率e =
= 1离心率e =![]() ……………………………5分
……………………………5分
(Ⅱ)由(Ⅰ)知A(1,0),F(3,0),
当直线PQ与x轴垂直时,PQ方程为x = 3 .此时,![]() ≠0,应舍去.
≠0,应舍去.
当直线PQ与x轴不垂直时,设直线PQ的方程为y = ( x – 3 ).
由方程组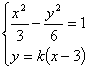 得
得
![]()
由一过点F的直线与双曲线交于P、Q两点,
则![]() -2≠0,即k≠
-2≠0,即k≠![]() ,
,
由于△=36![]() -4(
-4(![]() -2)(9
-2)(9![]() +6)
+6)
=48(![]() +1)>即k∈R.
+1)>即k∈R.
∴k∈R且k≠![]() (*) ……………………………………………………8分
(*) ……………………………………………………8分
设P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),则
),则
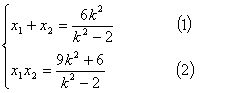
由直线PQ的方程得![]() = k(
= k(![]() -3),
-3),![]() = k(
= k(![]() -3)
-3)
于是![]()
![]() =
=![]() (
(![]() -3)(
-3)(![]() -3)=
-3)=![]() [
[![]()
![]() -3(
-3(![]() +
+![]() )+ 9] (3)
)+ 9] (3)
∵![]() = 0,
= 0,
∴(![]() -1,
-1,![]() )·(
)·(![]() -1,
-1,![]() )= 0
)= 0
即![]()
![]() -(
-(![]() +
+![]() )+ 1 +
)+ 1 + ![]()
![]() = 0
(4)
= 0
(4)
由(1)、(2)、(3)、(4)得
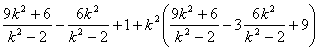 = 0
= 0
整理得![]() =
=![]() ∴k =
∴k =![]() 满足(*)
满足(*)
∴直线PQ的方程为x = ![]() -3 = 0或x +
-3 = 0或x +![]() -3 = 0……………………14分
-3 = 0……………………14分
21.(理)解:(1)![]() :y=x-1,a=-
:y=x-1,a=-![]()
(2)![]() 设
设![]()
![]() ,令
,令![]() ,得
,得![]()
| x |
| -1 |
| 0 |
| 1 |
|
|
| + | 0 | - | 0 | + | 0 | - |
|
|
| 极大值 |
| 极小值 |
| 极大值 |
|
所以1)当![]() 时有两个解
时有两个解
2)当![]() 时有3个解
时有3个解
3)当![]() 时有4个解
时有4个解
4)![]() 时有两个解
时有两个解
5)当![]() 时无解
时无解
(文)解:(1)![]() 又
又![]() ,
,![]() 分别对应函数取极小值和极大值,则-1,
分别对应函数取极小值和极大值,则-1,![]() 是方程
是方程![]() 的两根
的两根
所以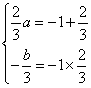
![]()
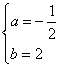 此时
此时![]()
当![]() 时,
时,![]() ,此时
,此时![]() 所以所求切线方程是:
所以所求切线方程是:![]()
即:![]()
(2)![]()
![]()
22.(文理)解(1)设P点的纵坐标为![]()
因为![]() 所以P是P1P2的中点,即
所以P是P1P2的中点,即![]() ,得
,得![]()
因为![]() 所以
所以![]()
(2)由(1)可知,当![]() 时,
时,![]()
又![]()
![]()
![]()
所以2![]()
又![]() 所以2
所以2![]()
![]()
![]()
(3)![]()
![]()
则![]()
所以![]()
因为![]() 所以
所以![]() 可变形为
可变形为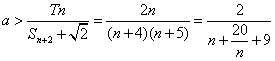
要使上不等式成立,只需要![]() 大于
大于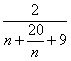 的最大值即可,令
的最大值即可,令![]() ,易知
,易知![]() 所以
所以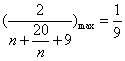 所以
所以![]()
