钦州市2006年高三毕业班第一次调研测试

理科数学（必修＋选修Ⅱ）

　　本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页．考试结束后，将本试卷和答题卡一并交回．共150分．考试时间120分钟．

第Ⅰ卷

注意事项：

1．答题前，考生在答题卡上务必用黑色签字笔将自己的姓名、准考证号填写清楚，并贴好条形码．请认真核准条形码上的准考证号、姓名和科目．

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．

3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

参考公式：

如果事件A、B互斥，那么 P（A＋B）＝P（A）＋P（B）．

如果事件A、B相互独立，那么 P（A·B）＝P（A）·P（B）．

如果事件A在1次试验中发生的概率是P，那么n次独立重复试验中恰好发生次的概率．

球的表面积公式 S_球＝4πR² 其中R表示球的半径．

球的体积公式 V_球＝πR³ 其中R表示球的半径．

一、选择题：

1．如图，U是全集，M、P、S是U的三个子集，则阴影部分所表示的集合是

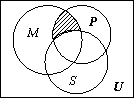（A）（MP）S

（B）（MP）S

（C）（MP）（_US）

（D）（MP）（_US）

2．设函数f（x）＝sin（πx－），则下列命题中正确的是

　（A）f（x）是周期为1的奇函数　　　　 （B）f（x）是周期为2的偶函数

（C）f（x）是周期为1的非奇非偶函数　　　　　　　　　　　　　　　　（D）f（x）是周期为2的非奇非偶函数

3．有如下三个命题：

①分别在两个平面内的两条直线一定是异面直线；

②垂直于同一个平面的两条直线是平行直线；

③垂直于同一个平面的两个平面互相平行；

④过平面的一条斜线有一个平面与平面垂直．

其中正确命题的个数为

　（A）1　　　　　　　　　　（B）2　　　　　　　　　　（C）3　　　　　　　　　　（D）4

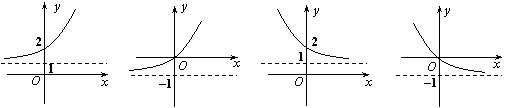4．函数y＝log（x－1）的反函数的图象是

　　　　　　　　　　　　　　　　　　　（A）　　　　　　　　　　（B）　　　　　　　　　　　　（C）　（D）

5．设abc≠0，“ac＞0”是“曲线ax²＋by²＝c为椭圆”的

　（A）充分非必要条件　　　　　　 （B）必要非充分条件

（C）充分必要条件　　　　　　　　（D）既非充分又非必要条件

6．已知向量、为单位向量，它们的夹角为60°，则＋3的值是

　（A）　　　　　　　　（B）　　　　　　　 （C）　　　　　　　（D）4

7．用1，2，3，4，5这五个数字，组成比20 000大，而且百位数字不是3的没有重复数字的五位数共有

　（A）64个　　　 （B）72个　　　 （C）78个　　　 （D）96个

8．等差数列｛a_n｝中，如a₁＋a₂＋a₃＝6，a₁₀＋a₁₁＋a₁₂＝9，则a₁＋a₂＋…＋a₁₂＝

　（A）15　　　　　　　　　（B）30　　　　　　　　　（C）45　　　　　　　　　（D）60

9．椭圆＝１，两焦点间距离为6，则t＝

　（A）16　　　　　　　　　（B）34　　　　　　　　　（C）16或34　　　　 （D）11

10．已知双曲线的两个焦点为F₁（－，0），F₂（，0），P是此双曲线上的一点，且PF₁⊥PF₂，PF₁·PF₂＝2，则该双曲线的方程

　（A）＝1　 （B）＝1　 （C）＝1　 （D）＝1

11．已知奇函数f（x）的定义域为：｛x｜｜x＋2－a｜＜a，a＞0｝，则a的值为

　（A）0　　　　　　　　　　（B）1　　　　　　　　　　（C）2　　　　　　　　　　（D）3

12．函数f（x）在上是增函数，A（０，－2）、B（4，2）是其图象上的两点，则不等式

f（x＋2）＜2的解集是

　（A）（－∞，－2）∪（2，＋∞）　　　（B）（－2，2）

（C）（－∞，0）∪（4，＋∞）　　　　　　（D）（0，4）

　钦州市2006年高三毕业班第一次调研测试

理科数学（必修＋选修Ⅱ）

第Ⅱ卷

题号	一	二	三						总分
			17	18	19	20	21	22
得分

注意事项：

1．用钢笔或圆珠笔直接答在试题卷中．

2．答卷前将密封线内的项目填写清楚．

3．本卷共10小题，共90分．

得分	评卷人

二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．

13．＝　　　　　　  ．

14．圆x²＋y²＋x－6y＋3＝0上两点P、Q关于直线kx－y＋4＝0对称，则k＝　　　　 ．

15．一个袋子里装有大小相同的3个红球和2个黄球，从中同时取出两个，则其中含红球个数的数学期望是_________________．

16．如图，正方体ABCD－A₁B₁C₁D₁的棱长为a，将该正方体沿对角面BB₁D₁D切成两块，再将这两块拼接成一个不是正方体的四棱柱，那么所得四棱柱的全面积为　　　　　　　 ．

三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．

得 分	评卷人

17．（本小题满分12分）

已知一扇形的周长为c（c＞0），当扇形的弧长为何值时，它有最大面积？并求出面积的最大值.

得 分	评卷人

18．（本小题满分12分）

从6位女同学和4位男同学中随机选出3位同学进行体能测试，每位女同学能通过测试的概率均为，每位男同学能通过测试的概率均为，试求：

（1）选出的3位同学中，至少有一位男同学的概率；

（2）10位同学中的女同学甲和男同学乙同时被选中且通过测试的概率．

19．（本小题满分12分）

得 分	评卷人

已知有三个居民小区A、B、C构成△ABC，AB＝700、BC ＝800、AC＝300．现计划在与A、B、C三个小区距离相等处建造一个工厂，为不影响小区居民的正常生活和休息，需在厂房的四周安装隔音窗或建造隔音墙．据测算，从厂房发出的噪音是85分贝，而维持居民正常生活和休息时的噪音不得超过50分贝．每安装一道隔音窗噪音降低3分贝，成本3万元，隔音窗不能超过3道；每建造一堵隔音墙噪音降低15分贝，成本10万元；距离厂房平均每25噪音均匀降低1分贝．

（1）求∠C的大小；

　　（2）求加工厂与小区A的距离．（精确到1）；

（3）为了不影响小区居民的正常生活和休息且花费成本最低，需要安装几道隔音窗，建造几堵隔音墙?

（计算时厂房和小区的大小忽略不计）

得 分	评卷人

20．（本小题满分12分）

如图①所示的等腰梯形ABCD中，上底和高均为2，下底边长为2＋2，DE⊥AB于E，CF⊥AB于F，将△AED、△BFC分别沿DE、CF折起，使A、B重合于P得图形②．在空间图形②中：

（1）求证：FP⊥平面PDE；

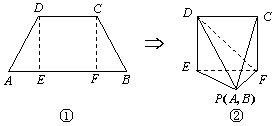（2）求EF与面PDF所成的角的大小．

21．（本小题满分13分）

得 分	评卷人

已知等比数列｛a_n｝中，a₁＝64，公比q≠1，a₂、a₃、a₄又分别是某等差数列的第7项、第3项、第1项．

（1）求等比数列｛a_n｝的通项公式a_n；

（2）设b_n＝log₂a_n，求数列｛b_n｝的前n项和．

22．（本小题满分13分）

得 分	评卷人

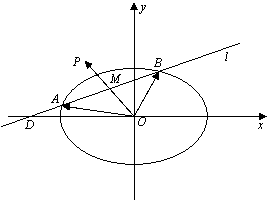如图，已知过点D（－2，0）的直线l 与椭圆＋y²＝1交于不同的两点A、B，点M是弦AB的中点．

（1）若＝＋，求点P的轨迹方程；

（2）求的取值范围．

　钦州市2006年高三毕业班第一次调研测试

理科数学参考答案及评分标准

说明：

1、如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．

2、对计算题，当考生的解答在某一步出错时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．

3、解答右端所注分数表示考生正确做到这一步应得的累加分数．

4、只给整数分．选择题和填空题不给中间分．

一、选择题：（每小题5分，共60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	B	B	C	B	C	C	B	C	D	C	B

二、填空题：（每小题4分，共16分）

13．　　　　　14．2　　　　　　15．　　　　　　　　 16．（4＋2）a²

三、解答题：

17．解：设扇形的半径为R，弧长为l，面积为S，

∵c＝2R＋l，∴R＝，（l＜c）．·················································································· 2分

则S＝Rl＝×·l＝（cl－l²）·········································································· 6分

＝－（l²－cl）＝－＋，································································ 8分

∴当l＝时，S_max＝．··································································································· 11分

答：当扇形的弧长为时，扇形有最大面积，面积的最大值是.············· 12分

18．解：（1）易知选出的3位同学中，没有选到一位男同学的概率是，·············· 4分

∴选出的3位同学中，至少有一位男同学的概率P＝1－＝；···· 6分

（2）除女同学甲和男同学乙同时被选中外还有另外的8个同学中有一位同学的概率是，　　 10分

∵每位女同学能通过测试的概率均为，

每位男同学能通过测试的概率均为，

∴10位同学中的女同学甲和男同学乙同时被选中且通过测试的概率

P＝××＝．····················································································· 12分

19．解：（1）由余弦定理得cos∠C＝，∠C＝60º；······························································· 3分

（2）由题设知，所求距离为△ABC外接圆半径R，················································· 4分

由正弦定理得R＝＝404．·········································································· 6分

答：加工厂与小区A的距离约为404；···························································· 7分

（3）设需要安装x道隔音窗，建造y堵隔音墙，总成本为S万元，由题意得：

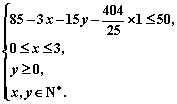即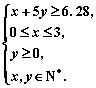····················································· 9分

其中S＝3x＋10y，当x＝2，y＝1时，S最小值为16万元．····················· 11分

答：需安装2道隔音窗，建造1堵隔音墙即可．··········································· 12分

20．解法一：

（1）在等腰梯形ABCD中，EF＝DC＝2，AE＝BF＝，·········································· 1分

而AE＝PE，BF＝PF，∴PE²＋FP²＝EF²，∴PF⊥EP．···································· 2分

又∵AE⊥DE（即PE⊥DE），EF⊥DE，∴DE⊥面PEF，·································· 4分

∴DE⊥FP，∴FP⊥面PDE；···························································································· 6分

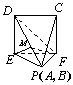（2）由（1）得FP⊥面PDE，∴面FPD⊥面PDE，························· 7分

作EM⊥DP于M，则EM⊥面PDF，················································ 8分

连结FM，则∠EFM为EF与面PDF所成的角．························ 9分

在△PED中，＝，可得，EM＝＝，························ 10分

∴sin∠EFM＝＝＝，∴∠EFM＝arcsin．························ 11分

故EF与面PDF所成的角的大小为arcsin．····················································· 12分

解法二：

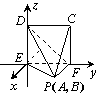
（1）以E为坐标原点，建立如图所示的空间直角坐标系E－xyz，························· 1分

则依题意得D（0，0，2），C（0，2，2），F（0，2，0），P（1，1，0），· 2分

∴＝（1，－1，0），＝（0，0，2），＝（－1，－1，2）．·········· 3分

∵·＝（1，－1，0）·（0，0，2）＝0··························· 4分

·＝（1，－1，0）·（－1，－1，2）

＝－1＋1＋0＝0，································································ 5分

∴FP⊥ED，FP⊥PD，∴FP⊥平面PDE；······························ 6分

（2）设面PDF的法向量＝（x，y，z），则

即∴············································· 8分

取y＝2，则＝（2，2，2）．······························································································ 9分

设EF与面PDF所成的角为，则＝·sin，················· 10分

∴sin＝＝，＝arcsin．····························· 11分

故EF与面PDF所成的角的大小为arcsin．······················································· 12分

21．解：（1）∵＝，∴＝，·············································· 2分

2q²－3q＋1＝0，∴q＝，··························································································· 4分

∴a_n＝2；························································································································· 6分

（2）b_n＝log₂a_n＝log₂2＝7－n，····················································································· 8分

∴当1≤n≤7时，

b₁＋b₂＋…＋b_n＝b₁＋b₂＋…＋b_n＝（13n－n²）;······················· 10分

∴当n≥8时，

b₁＋b₂＋…＋b_n＝（b₁＋b₂＋…＋b₇）－（b₈＋b₉＋…＋b_n）····· 11分

＝2（b₁＋b₂＋…＋b₇）－（b₁＋b₂＋…＋b_n）····· 12分

＝42－（13n－n²）．····················································· 13分

22．解：（1）设直线l的方程为y＝k（x＋2），P（x，y），A（x₁，y₁），B（x₂，y₂）， 1分

由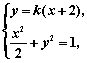得：（1＋2k²）x²＋8k²x＋8k²－2＝0，··································· 3分

∴△＝64k⁴－4（1＋2k²）（8k²－2）＞0，∴0≤k²＜．······························ 4分

∵＝＋，

∴x＝x₁＋x₂＝－，y＝y₁＋y₂＝k（x₁＋x₂＋4）＝，········ 5分

消去k得：x²＋2y²＋4x＝0，························································································ 6分

又x＝－＝－4＋∈，

∴点P的轨迹方程为：x²＋2y²＋4x＝0，（－2＜x≤0）；······························ 7分

（2）＝＝＝····································· 9分

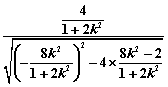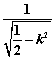＝＝··············································· 11分

∵0≤k²＜，∴∈．································································· 13分