2006届清华大学自主招生数学试题

考试时间：2005.11.28

1．求最小正整数，使得为纯虚数，并求出．

2．已知为非负数，，求的最值．

3．已知为等差数列，为等比数列，求的值．

4．求由正整数组成的集合，使中的元素之和等于元素之积．

5．随机取多少个整数，才能有0.9以上的概率使得这些数中至少有一个偶数．

6．上一点(非原点)，在P 处引切线交轴于，求．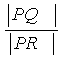

7．已知满足：对实数有，且，求证恒为零．

(可用以下结论：若，为一常数，那么)

8．在所有定周长的空间四边形中，求对角线和的最大值，并证明．