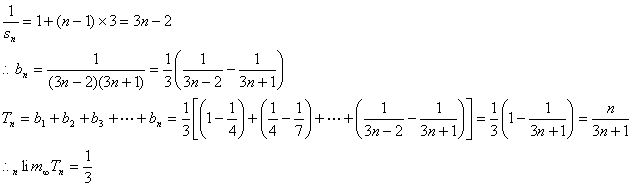2004全国重点中学临考仿真试卷

数　学（第一模拟）

班级　　　　  姓名　　　　　 得分

题号	一	二	三	总分
分数

第1卷（选择题　共和60分）

得分

一. 选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

 

1.时,z¹⁰⁰+z⁵⁰+1 的值勤等于(　　)

A.　　  1　　　　　　  B　-1　　　　　　　 C　i　　　　　　　　D　-I

2.已知,则的值为(　　)

A.　　　　　　 B.　　　　　　　  C.　　　　　　　 D.3

3.函数y=6-x+的值域是(　　)

A.　　　　B.　　　　C.　　　　 D.

4.若实数x . y满足(x+5)²+(y-12)²=14²  ,则x²+y²的最小值为(　　)

A.2　　　　　　　　 B.1　　　　　　　  C.　　　　　　　 D.

5.若O为坐标原点,抛物线y²=2x与过其焦点的直线交于A . B两点,则OA · OB等于　(　　)

A.　　　　　　　  B.-　　　　　　  C.3　　　　　　　　 D.-4

6.若一个等差数列前3项的和为34, 最后3项的和为146,　且所有项的和为390 , 则此数列的项数为(　　)

A.13　　　　　　 　 B.12　　　　　　　 C.11　　　　　　　  D.10

7.曲线f(x)=x⁴-x在点P的切线平行于直线3x-y=o,　 则P点坐标为 (　　)

A.(1, 3)　　　　　　  B.(-1, 3)　　　　　  C.(1, 0)　　　　　　 D(-1, 0)

8.若一个长方体的全面积为22,　体积是8,　则这样的长方体(　　)

Ａ. 有一个别　　　　 Ｂ. 有两个别　　　 Ｃ. 有无数多个别　　Ｄ. 不存在

9.已知f (x) = a^x(a>0且a1),　f^-1(2)<0,　则f^-1(x+1)的图像是图1中的(　　)

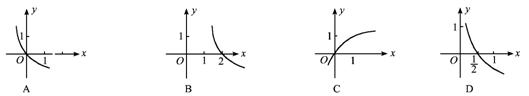
图１

10. 的值为　(　　)

A.　　　　　　　　 B.　　　　　　　 C.　　 　　　　　 D.1

11.在平行六面体中,过交于同一点的三条棱的中点的平面截此六面体,则所截三棱锥的体积的(　　)

A.　　　　　　　　 B.　　　　　　  C.　　　　　　　  D.

12.正方形ABCD中, AB. CD的中点分别为EF, BD与EF的交点是O(如图2甲所示).以EF为棱将正方形ABCD折成直二面角时(如图2乙所示),则BOD的大小是(　　)

A.150^o　　　　　　　 B.135^o　　　　　　  C.120^o　　　　　　　  D.90^o

图2

得分

二.填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.

13.若的展开式中含x的项为第6项,设,则　　　　　　　 .

14.  一个工厂有若于个车间,今采用分层抽样方法从全厂某天的2048件产品中抽取一个容量为128的样本进行质量检查.若一车间这一天生产256件产品,则从该车间抽取的产吕件数

为　　　　　　　 .

15.从6名运动员中选取4名参加4×400m接力赛,如果甲不跑第一棒,乙不跑第四棒,不同的参赛方案有　　　　　　 种.(用数字作答)

16.已知一个球的内接正方体的表面积为S,那么这个球的半径等于　 　　　　　 .

三.解答题：本大题共6小题，共74分。解答应定出文字说明 证明过程或演算步骤。

得分

17．（本小题满分12分）

已知函数为常数）.

（1）　　　 求函数的最小正周期；

（2）　　　 求函数的音调递减区间；

（3）　　　 若时，f(x)的最小值为-2，求a的值。

18．（本小题满分12分）

如图3所示，在空间直角坐标系中，空间四面体的四个顶点分别为O（0，0，0），A（4，0，0），B（3，2，0），P（1，4，1），R，S是PA的三等分点，M .N分别是PB. OB的中点，求:　

（1）　　　 直线NR和MS的夹角的余弦值；

（2）　　　 二面角P-OA-B的余弦值。

19．（本小题满分12分）

已知，求(x+y)²⁰⁰⁴的值。

20．（本小题满分12分）

一台设备由三大部件组成，在设备运转中，各部件需要调整的概率相应为0，1，0，2，3，假设各部件的状态相互独立，以  表示同进需要调整的部件数。试求的数学期望E。

21．（本小题满分12分）

如图4所示，A₁ .A为椭圆的两个顶点，F₁.F₂为椭圆的两个焦点。　　　　　　　　　　　　　　　　　　　　　　　

图4

（1）　　　 写出椭圆的方程及其准线方程；

（2）　　　 过线段OA上异于O. A的任一点K作OA的垂线，交椭圆于P. P₁两点，直线A₁P与AP₁交于点M。

求证：点M在双曲线上。

22．（本小题满分14分）

设数列前n项的和为S_n，已知a₁=1，且满足.

(1).求证：是等差数列;

（3）　　　 设，数列的前n项和为T_n，求。

答案及要点解析

数　学(第一模拟)

一.　 选择题

1.　　　 D　 2.D　 3B　 4.B　 5.B　 6.A　 7.C　 8.D　 9.A　 10.A　 11.D　 12.C

二.　 填空题

13.255　　　　　　　　　　　

14.16

15.252

16.

三.　 解答题

17.解(1)

的最小正周期

(2)当即时，函数f(x)单调递减，故所求区间为

（３）时，时，f(x)取得最小值

18. 解：（１）Ｍ、Ｎ分别是PB、OB的中点M点的坐标为，Ｎ点的坐标为设Ｒ的坐标为(x₁,y₁,z₁)

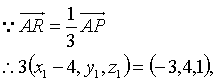
Ｒ的坐标为

　　 设Ｓ的坐标为

　　 的坐标为

设NR和MS之间的夹角为, 　　　　　　　　　　　

则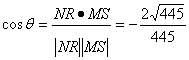

所以直线NR和MS的夹角的余弦值为

(2).设点Ｐ在平面xOy内的射影为点Ｑ，则点Ｑ的坐标为(1,4,0)，点Ｑ在OA上的射影D的坐标为(1,0,0)

　　　 PDQ为二面角P-OA-B的平面角

DP=(0,4,1),　DQ=(0,4,0)

设DP与DQ间的夹角为则

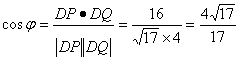
所求二面角的余弦值为。

19．解：要使有意义，必须1-2004x≥0即x≤综合上述，必须,这时所以

20.解：设事件A_i =, I=1,2,3则由题意, ξ可能有四个值0,1,2,3,由于各事件A_i相互独立，故

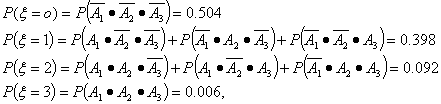
即　　　　

ξ	0	1	2	3
P	0.504	0.398	0.092	0.006

21. (1).解：由图可知a=5, c=4所以该椭圆的方程为

准线方程为

(2). 证明：设Ｋ点坐标为 (x₀, 0) ,　点P 。P₁的坐标分别记为（x₀, y₀）、(x₀, -y₀) ，

其中0<x₀<5则　　　　　 ①　直线A₁P、P₁A的方程分别为：

②式除以③式得化简上式得，代入②式得于是，

直线A₁P与AP₁的交点M的坐标为

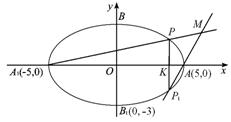
第21题图

因为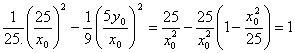所以直线A₁P与AP₁的交点M在双曲线上。

22．（1）证明：是以为.

(2).解：由(1)得