江苏省栟茶高级中学高三数学综合练习一

本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分。考试时间120分钟.

注意事项：

1. 答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2. 每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3. 考试结束，监考人将本试卷和答题卡一并收回。

参考公式：

　 ①如果事件A、B互斥，那么

　 ②如果事件A、B相互独立，那么

③如果事件A在一次试验中发生的概率是p，那么n次独立重复试验中恰好发生k次的

概率　

　　④球的表面积公式（其中R表示球的半径）

　　⑤球的体积公式（其中R表示球的半径）

第I卷（选择题，共60分）

一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题意的）

1．已知数列，“对任意的，点都在直线y=3x+2上”是“为等差数列”的　　　　　　　 （　A  ）

　　　 A．充分而不必要条件　　　　　　　　　　　　　　 B．必要而不充分条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

2．将函数的图象按向量平移后所得图象的解析式是（ A　）

　　　 A．　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　 D．

3．将一张坐标纸折叠，使得点（0，2）与点（－2，0）重合，且点（2004，2005）与点（m，n）重合，则m－n的值为　　　　　　　　　　　　　　　　　　 （ B ）

　　　 A．1　　　　　　　　　　　　B．－1　　　　　　　　　　 C．0　　　　　　　　　　　　D．2006

4．已知平面α、β、γ，直线，给出下列四个结论：①；②；③；④.则其中正确的个数是　　　　　　　　（ C ）

　　　 A．0　　　　　　　　　　　　B．1　　　　　　　　　　　　C．2　　　　　　　　　　　　D．3

5．如图，在△ABC中，，AC、BC边

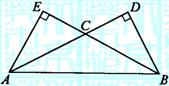
 上的高分别为BD、AE，则以A、B为焦点，且过D、E的

 椭圆与双曲线的离心率的倒数和为　　　　　　 （　A  ）

　　　 A．　　　　　　　　　　B．1　　　　　　　　　　　　C．　　　　　　　　　D．2

6．从6人中选出4人加数、理、化、英语比赛，每人只能参加其中一项，其中甲、乙两人

　 都不能参加英语比赛，则不同的参赛方案的种数共有　　　　　　　　　　　　　　　　　　　　（ C ）

　　　 A．96　　　　　　　　　　　B．180　　　　　　　　　　 C．240　　　　　　　　　　 D．288

7．11¹²除以100的余数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 D ）

　　　 A．1　　　　　　　　　　　　B．10　　　　　　　　　　　 C．11　　　　　　　　　　　 D．21

8．给出平面区域（包括边界）如图所示，若使目标函数

 取得最大值的最优解有无穷多个，

 则a的值为　　　　　　　　　　　　　  （B　　）

　　　 A．　　　　　　　　　　　B．

　　　 C．4　　　　　　　　　　　　D．

9．如右图，正方体ABCD—A₁B₁C₁D₁中，E、F分别是

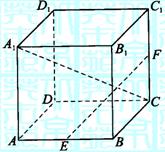
　 AB、CC₁的中点，则异面直线A₁C与EF所成角的余

　 弦值为　　　　　　　　　　　　　　　  （ B　 ）

　　　 A．　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　D．

10．函数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　B）

　　　 A．在处有极值　　　　　　　　　　　　 B．在处有极值

　　　 C．在处有极值　　　　　　　　　　　　　 D．在处都有极植

11．已知：是R上的增函数，点A（1，3），B（－1，1）在它的图象上，为它的反函数，则不等式的解集是　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ B ）

A．（1，3）　　　　　　　B．（2，8）　　　　　　　C．（－1，1）　　　　　D．（2，9）

12．已知椭圆E的离心率为e，两焦点为F₁、F₂，抛物线C以F₁为顶点，F₂为焦点，P为两曲线的一个交点，若，则e的值为　　　　　　　　　　　　　　　　　　　　　　　（ A　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　　 D．

第Ⅱ卷（非选择题　共90分）

二、填空题：本大题共4小题，每小题4分，共16分. 将每小题的答案直接填在题中所给的横线上）

13．若在的展开式中x的系数是6，则a=　　　－1　　　　.

14．圆心在（2，－3）点，且被直线截得的弦长为的圆的标准方程为

　　　　　　　　　　 .

15．如果三位数的十位数字大于百位数字，也大于个位数字，则这样的三位数一共有　　 

　　　　　240　　　　　　 .（作数字作答）

16．下面有4个命题：

　　①若a、b为一平面内两非零向量，则a⊥b是a+b=a－b的充要条件；

　　　 ②一平面内的两条曲线的方程分别是，它们的交点是，则方程的曲线经过点P；

　　　 ③经过一点且和一条已知直线垂直的所有直线都在同一平面内；

　　　 ④已知是抛物线上不同的两个点，则是直线AB通过抛物线焦点的必要不充分条件.

　　其中真命题的序号是　　　　 ①②③　　　 （把符合要求的命题序号都填上）

三、解答题：本大题共6小题，共74分，解答应写出文字说明证明过程或推演步骤.

17．（本小题满分12分）已知函数.

　 （1）求的最小值；

　 （2）求的单调递增区间.

17．解：（1）

，

　 （2）由　的单调增区间的

18．（本小题满分12分）

　　　　某学校的生物实验室里有一个鱼缸，里面有6条鱼，其中4条黑色的和2条红色的，有位生物老师每周4天有课，每天上、下午各一节课，每节课前从鱼缸中任意捞取1条鱼在课上用，用后再放回鱼缸.

　 （1）求这位生物老师在一天中上、下午所捞的鱼为同色的概率；

　 （2）求这位生物老师一周中恰有两天上、下午所捞得的鱼为不同色的概率.

18．解：（1）设一天同为黑色鱼的概率为P₁，同为红色鱼的概率为P₂，

则

答：这位生物老师在一天中上、下午所捞的鱼为同色的概率为

（2）有两个不同色的概率为

答：这位生物老师一周中恰有两天上、下午所捞得的鱼为不同色的概率为

19．（本小题满分12分）

如图，在底面是菱形的四棱锥P—ABCD中，∠ABC=60°，PA⊥平面ABCD，点E、F、G分别为CD、PD、PB的中点.

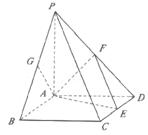
　 （1）证明PC//平面FAE；

　 （2）若PA=AD，求二面角F—AE—D的大小；

　 （3）为何值时，GA⊥平面FAE？证明你的结论.

19．（1）证明：因为E、F分别为△DCP中CD、PD边的中点，所以PC//EF.

　　　　 又PC平面FAE，EF平面FAE，所以PC//平面FAE.

　　　  AD=AC. 在ACD中，由E是CD中点，

　 　　 ∴有CD⊥AE.

　　　　　　　设H、M分别为AE、AD的中点，连结FM、MH.

　　　　因为点F是PD的中点，所以FM//PA，MH//DE.

　　　　由PA⊥平面ABCD，知FM⊥平面ABCD.

　　　　由CD⊥AE，知：MH⊥AE.

　　　　　　　连结FH，则FH⊥AE，所以∠FHM即为所求二面角的平面角.

　　　　设PA=AD=1，则

　　　　在Rt△FMH中，

　　　　所以

　 （3）解：当.

　　　　由（2）可知：CD⊥AE，又AB//CD，所以AB⊥AE.

　　　　由PA⊥平面ABCD，知PA⊥AE.

　　　　又PA∩AB=A，所以AE⊥平面PAB. 又GA平面PAB，所以GA⊥AE.

　　　　所以，要使GA⊥平面FAE，只需GA⊥AF.

在Rt△PAB中，设PA=x，AB=AD=y. 则AG=

同理

在△GAF中，令AG²+AF²=GF²，解得.

所以，当时，GA⊥平面FAE.　　　　　　　　　　　　　　

20．（本小题满分12分）

设数列是等差数列，a₁=1，其前n项和为S_n，数列是等比数列，b₂=4，其前n项和为T_n，又已知

　 （Ⅰ）求数列，的通项公式；

　 （Ⅱ）若的最大值及此时n的值.

20．解：，

∴　 

设的公差为d，∵∴5+10d=2（8+4）+1，d=2，

∴a_n=1+2(n－1)=2n－1.　  

（Ⅱ）∵

　 

当时，即n=3或n=4时，　 

　 

21．（本小题满分12分）

已知实数集R上的函数其中a、b、c、d是实数.

　 （Ⅰ）若函数在区间上都是增函数，在区间（－1，3）上是减函数，并且，求函数的表达式；

　 （Ⅱ）若a、b、c满足求证：函数是单调函　

∴　∵函数在区间上都是增函数，

在区间（－1，3）上是减函数，　∴－1和3必是的两个根，　 

∴　∴.　 

（Ⅱ）由条件

为二次三项式，并且

∴当a>0时，>0恒成立，此时函数是单调增函数，

当a<0时，<0恒成立，此时函数是单调减函数，

∴对任意给定的非零实数a，函数总是单调函数.  

22．（本小题满分12分）

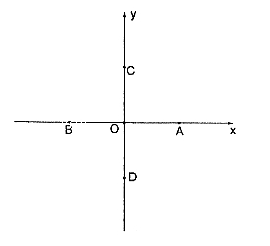　　　 在直角坐标系XOY中，已知点A（1，0），，C（0，1），，动点M满足，其中m是参数（）

　　（Ⅰ）求动点M的轨迹方程，并根据m的取值讨论方程所表示的曲线类型；

　　（Ⅱ）当动点M的轨迹表示椭圆或双曲线，且曲线与直线交于不同的两点

时，求该曲线的离心率的取值范围.

22．解：（I）设动点M的坐标为（x，y）

　　由题意得

　　　　　　　　　　　

　　

　　

　　动点M的轨迹方程为　　　　　　　　　　　　　　　　　　　　　　　

　　当时，，即，动点M的轨迹是一条直线；

　　当时，方程可以化为：

　　此时，当时，动点M的轨迹是一个圆；

　　当，或时，动点M的轨迹是一个椭圆

　　当时，动点M的轨迹是一条双曲线　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

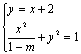　　（II）当且时，由得

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　

　　与该圆锥曲线交于不同的两个点

　　

　　即

　　且或　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　（1）且时，圆锥曲线表示双曲线

　　其中，

　　且　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

 （2）当时，该圆锥曲线表示椭圆：

　　其中

　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……12分

　　综上：该圆锥曲线的离心率e的取值范围是