江苏省南通中学高三数学调研试卷(06.4)
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共4页,满分150分,考试时间为120分钟
2.请将第I卷的答案填涂在答题卡上,第II卷的解答写在答题卷上,在本试卷上答题无效。
第I卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的
1.设集全A=![]() ,则集合A∩B= ( )
,则集合A∩B= ( )
A.![]() B.
B.![]() C.
C.![]() D.B
D.B
2.函数f(X)=![]() 的图像相邻两条对称轴之间的距离是( )
的图像相邻两条对称轴之间的距离是( )
A.![]() B.5π C.
B.5π C.![]() D.
D.![]()
3.过A(1,1)可作两条直线与圆![]() 相切,则k的范围为( )
相切,则k的范围为( )
A.![]() >0 B.
>0 B.![]() >4或0<
>4或0<![]() <1 C.
<1 C.![]() >4或
>4或![]() <1 D.
<1 D.![]() <0
<0
4.设A、B是两个非空集合,定义A与B差集为A-B={xx∈A,且x![]() B},则A-(A-B)等于( )
B},则A-(A-B)等于( )
A.A B.B C.A![]() B D.A
B D.A![]() B
B
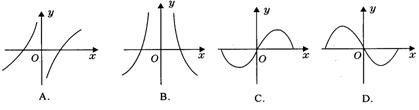
5.函数f(x)、函数g(x)的图像如图:

则函数y=f(x)·g(x)的图像可能是: ( )
6.在正数数列{![]() }中,a1=2,且点(
}中,a1=2,且点(![]() )在直线x-
)在直线x-![]() 上,前n项和
上,前n项和![]() 等于( )
等于( )
A. ![]() -1 B.2n+1-2 C.
-1 B.2n+1-2 C.![]() D.
D.![]()
7.在△ABC中,有命题:①![]() ②
②![]()
③若(![]() )·(
)·(![]() )=0,则△ABC为等腰三角形;
)=0,则△ABC为等腰三角形;
④若![]() 则△ABC为锐角三角形.上述命题正确的是( )
则△ABC为锐角三角形.上述命题正确的是( )
A.①② B.①②③ C. ②③ D.②③④
8.已知函数f(x)=1+logax(a>0,a≠1),满足f(9)=3,则f-1(log92)的值是( )
A.-1+log3![]() B.
B.![]() C.
C. ![]() D.
D.![]()
9.设直线![]() :2x+y+2=0关于原点对称的直线为
:2x+y+2=0关于原点对称的直线为![]() ,若
,若![]() 与椭圆x2+
与椭圆x2+![]() 有两交点为A、B,点P为椭圆上的动点,则使△PAB的面积为
有两交点为A、B,点P为椭圆上的动点,则使△PAB的面积为![]() 的点P的个数为( )
的点P的个数为( )
A.1 B.2 C.3 D.4
10.已知两个实数集A={a1,a2,…,a50}, B={b1,b2…,b25},若从A到B的映射f使得B中每个元素都有原象,且f(a1)≥f(a2)≥…≥f(a50),则这样的映射共有( )个
A.C![]() B.C
B.C![]() C.C
C.C![]() D.C
D.C![]()
x第II卷(tx非选择题,共100分)
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在答题卷相应位置上
11. 某中学有高一学生400人,高二学生300人,高三学生300人,现通过分层抽样抽取一样本容量为n的样本,已知每个学生被抽到的概率为0.2,则![]() ____________。
____________。
12. 数列![]() 满足:
满足:![]() ,,且
,,且![]() ,则
,则![]() 。
。
13.半径为1的球面上有三点A,B,C,若A和B,A和C,B和C的球面距离都是![]() ,过A、B、C三点做截面,则球心到面的距离为____________.
,过A、B、C三点做截面,则球心到面的距离为____________.
14. 若指数函数![]() 的部分对应值如下表:
的部分对应值如下表:
|
| -2 | 0 | 2 |
|
| 0.694 | 1 | 1.44 |
则不等式![]() 的解集为
。
的解集为
。
15. 设命题p: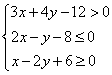 (x、y∈R),命题q:
(x、y∈R),命题q:![]() (x、y、r∈R,r>0),
(x、y、r∈R,r>0),
若命题q是命题¬p的充分非必要条件,则r的最大值为__________.
16. P、Q是抛物线y=x2上顶点以外的两点,O为坐标原点.∠POQ=![]() ,直线
,直线![]() 、
、![]() 分别是过P、Q两点抛物线的切线.(Ⅰ)则
分别是过P、Q两点抛物线的切线.(Ⅰ)则![]() 、
、![]() 的交点M点的轨迹方程是
;(Ⅱ)若
的交点M点的轨迹方程是
;(Ⅱ)若![]() 、
、![]() 分别交x轴于A、B两点,则过△ABM的垂心与点
分别交x轴于A、B两点,则过△ABM的垂心与点![]() 的直线方程是
的直线方程是
.
三、解答题:本大题共5小题,共70分,请把解答写在答题卷规定的答题框内,解答应写出文字说明,证明过程或演算步骤
17.(本小题满分12分) 在三角形ABC中,a、b、c分别是角A、B、C对边的长,且满足![]() .(Ⅰ)求角B的值;(Ⅱ)若b=
.(Ⅰ)求角B的值;(Ⅱ)若b=![]() ,
,![]() =5,求a、c值.
=5,求a、c值.
18.(本小题满分14分)已知函数f (x)满足f (logax)=![]() ,其中a>0且a≠1.(1)对于函数f (x),当x∈(-1, 1)时,f (1-m)+f (1-m2)<0,求实数m值的集合;(2)当x∈(-∞, 2)时,f (x)-4值恒为负数,求a的范围.
,其中a>0且a≠1.(1)对于函数f (x),当x∈(-1, 1)时,f (1-m)+f (1-m2)<0,求实数m值的集合;(2)当x∈(-∞, 2)时,f (x)-4值恒为负数,求a的范围.
19.
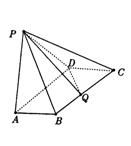
(本小题满分14分)如图:四棱锥P-ABCD中,底面ABCD是矩形,AB=![]() ,BC=a,又PA⊥平面ABCD,PA=4.(Ⅰ)若在边BC上存在一点Q,使PQ ⊥QD,求a的取值范围;(Ⅱ)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
,BC=a,又PA⊥平面ABCD,PA=4.(Ⅰ)若在边BC上存在一点Q,使PQ ⊥QD,求a的取值范围;(Ⅱ)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
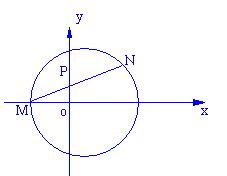
20.(本小题满分14分)如图,已知圆C:![]() ,设
,设![]() 为圆C与
为圆C与![]() 轴左半轴的交点,过
轴左半轴的交点,过![]() 作圆C的弦
作圆C的弦![]() ,并使它的中点P恰好落在
,并使它的中点P恰好落在![]() 轴上。(1)当
轴上。(1)当![]() 时, 求满足条件的P点的坐标;
时, 求满足条件的P点的坐标; ![]() (2)当
(2)当![]() 时,求N的轨迹G方程;
(3)过点P(0,2)的直线
时,求N的轨迹G方程;
(3)过点P(0,2)的直线![]() 与(2)中轨迹G相交于两个不同的点
与(2)中轨迹G相交于两个不同的点![]() ,若
,若![]() ,求直线
,求直线![]() 的斜率的取值范围。
的斜率的取值范围。
21. (本小题满分16分)已知等差数列![]() 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列![]() 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,![]() ,且
,且![]() .(1)求a的值;(2)若对于任意
.(1)求a的值;(2)若对于任意![]() ,总存在
,总存在![]() ,使
,使![]() ,求b的值;(3)在(2)中,记
,求b的值;(3)在(2)中,记![]() 是所有
是所有![]() 中满足
中满足![]() ,
, ![]() 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记![]() 为
为![]() 的前n项和,
的前n项和,![]() 是
是![]() 的前n项和,求证:
的前n项和,求证:![]() ≥
≥![]()
![]()
高三数学综合训练(一)参考答案
选择题1.A 2.D 3.B4.C 5A .6.B 7.C 8.B 9.B 10.B
填空题11.200 12。![]() 13.
13.![]() 14.
14.![]() 15。
15。![]()
16.![]()
解答题 17.解:(Ⅰ)由正弦定律有:
![]()
代入![]()
即:2sinAcosB+sinCcosB+sinBcosC=0
2sinAcosB+sin(C+B)=0
在△ABC中,有A+B+C=π 即:sinA=sin(B+C)
∴2sinAcosB+sinA=0,
∵sinA≠0
∴cosB=-![]()
![]()
(Ⅱ)由余弦定律有:b2=a2+c22accosB=(a+c)2-2ac(1+cosB)
19=(5)2-2ac(1-![]()
![]()
18.解:分析:先求出函数解析式,再转化为可比较的函数,利用正数单调性求解.
解:令logax=t(t∈R),则x=at,∵f(t)=(at-a-t)
∴f(x)=(ax-a-x)(x∈R),易证得f(x)在R上是递增的奇函数.
(1)由f(1-m)+f(1-m2)<0,及f(x)为奇函数,得f(1-m)<f(m2-1)
再由f(x)的单调性及定义域,得-1<1-m<m2-1<1,解得1<m<.
(2)∵f(x)是R上的增函数,∴f(x)-4在R上也是增函数,
由x<2,得f(x)<f(2),要使f(x)-4在(-∞,2)上恒为负数,
只需f(2)-4≤0,而(a2-a-2)≤0
解得:2-≤a≤2+且![]() .
.
19. (Ⅰ)解:设BQ=t,AQ2=3+t2,则PQ2=19+t2,
QD2=3+(a-t)2,PD2=16+a2
由PQ⊥QD得:19+t2+3+(a-t)2=16+a2,即t2-at+3=0
∴△a2-12≥0![]()
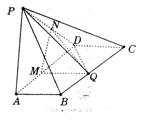 (Ⅱ)解:由(2)得当a=4时,t2-4t+3=0,t=1或t=3因为面PAD⊥面ABCD,所以过Q作 QM⊥AD,则QM⊥面PAD, 过M作MN⊥PD,由三垂线定理有QN⊥PD所以∠NNQ是三面角A-PD-Q的平面角在Rt△PAD中,
(Ⅱ)解:由(2)得当a=4时,t2-4t+3=0,t=1或t=3因为面PAD⊥面ABCD,所以过Q作 QM⊥AD,则QM⊥面PAD, 过M作MN⊥PD,由三垂线定理有QN⊥PD所以∠NNQ是三面角A-PD-Q的平面角在Rt△PAD中,
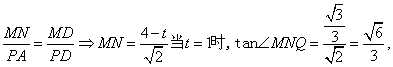
∴二面角A-PD-Q的大小为arctan![]()
20. 解:(1)解法一:由已知得,![]() 时,可求得
时,可求得![]() 点的坐标为(-1,0),
点的坐标为(-1,0),
设P(0,b),则由![]() (或用勾股定理)得:
(或用勾股定理)得:![]() ,所以
,所以![]() 即点P坐标为
即点P坐标为![]() 。
解法二:同上可得
。
解法二:同上可得![]() ,设
,设![]() 则
则
![]() 解得
解得![]() 。所以
。所以![]() 的中点P坐标为
的中点P坐标为![]() 。
。
(2)解法一:设![]() 由已知得,在圆方程中令y=0,求得
由已知得,在圆方程中令y=0,求得![]() 点的坐标为
点的坐标为![]() 。设P(0,b),则由
。设P(0,b),则由![]() (或用勾股定理)得:
(或用勾股定理)得:![]() 。
。
因为点P为线段![]() 的中点,所以
的中点,所以![]() ,
,![]() ,又r>1
,又r>1
所以点N的轨迹方程为![]() 。
。
解法二:设N(x,y),同上可得![]() ,则
,则
![]() ,消去r,又r>1,所以点N的轨迹方程为
,消去r,又r>1,所以点N的轨迹方程为![]() 。
。
(3)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
![]()
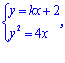 消去
消去![]()
![]() 因为直线
因为直线![]() 与抛物线
与抛物线![]() 相交于两个不同的点
相交于两个不同的点![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,
所以![]()
综上可得![]() 。
。
21. 解:(1)∵ ![]() ,a,
,a,![]() ,
,
∴ ![]() ∴
∴ 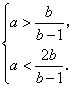 ∴
∴ 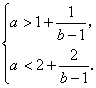
∴ ![]() .
∴ a=2或a=3(a=3时不合题意,舍去). ∴a=2.
.
∴ a=2或a=3(a=3时不合题意,舍去). ∴a=2.
(2)![]() ,
,![]() ,由
,由![]() 可得
可得
![]() . ∴
. ∴ ![]() . ∴ b=5
. ∴ b=5
(3)由(2)知![]() ,
,![]() , ∴
, ∴ ![]() .
.
∴ ![]() . ∴
. ∴ ![]() ,
,![]() .
.
∵ ![]() ,
,![]() .
.
当n≥3时,
![]()
![]()
![]()
![]() .
.
∴ ![]() . 综上得
. 综上得 ![]()
![]()