高三文科复习作业(21)
班级 姓名 座号
1、已知m、n为两条不同的直线α、β为两个不同的平面,给出下列四个命题
①若m![]() α,n//α,则m//n ; ②若m⊥α,n//α,则m⊥n;
α,n//α,则m//n ; ②若m⊥α,n//α,则m⊥n;
③若m⊥α,m⊥β,则α//β; ④若m//α,n//α,则m//n.
其中真命题的序号是 ( )
A.①② B.③④ C.①④ D.②③
2、已知函数![]() 和
和![]() ,其中
,其中![]() ,则它们反函数的图象关于 ( )
,则它们反函数的图象关于 ( )
A.x轴对称 B.y轴对称 C.直线![]() 对称 D.原点对称
对称 D.原点对称
3、已知数列![]() 前n项之和,则使Sn<-5成立的自然数n的 ( )
前n项之和,则使Sn<-5成立的自然数n的 ( )
A.最小值为31 B.最大值为31 C.最小值为63 D.最大值为63
4、已知点![]() , 又
, 又![]() 是曲线
是曲线![]() 上的点, 则 ( )
上的点, 则 ( )
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
5、已知球O的一个截面的面积为![]() , 球心O到这个截面的距离为1, 则该球的体积为 .
, 球心O到这个截面的距离为1, 则该球的体积为 .
6、事件A、B、C相互独立,如果![]() ,则P(B)=
;
,则P(B)=
;![]() =
.
=
.
7、已知命题p:偶函数![]() 内是增函数,且
内是增函数,且![]() ,命题
,命题![]()
![]() 是减函数,若p或q为真命题,p且q为假命题,则实数m的取值范围是
.
是减函数,若p或q为真命题,p且q为假命题,则实数m的取值范围是
.
8、代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将以40千米/时的速度向正北方向移动,离台风中心350千米的范围都会受到台风影响,则A码头从受到台风影响到影响结束,将持续多少小时________.
9、设f(x)是[-2,2]上的偶函数,且在[0,2]上是单调递减的,若f(1-m)<f(m),求m取值范围.
10、点A到直线l的距离为2a (a>0),P为l上一动点,过P点作l的垂线交线段AP的垂直平分线于Q.
(1)求Q点的轨迹方程;
(2)若点B到l的距离为a+4,AB⊥l,且A、B在l的同侧,过点B作直线交(1)中的轨迹于M、N,当![]() 时,求a的取值范围;
时,求a的取值范围;
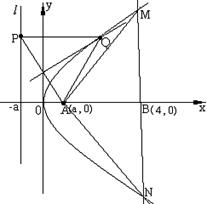 (3)求(2)中线段MN的中点轨迹方程.
(3)求(2)中线段MN的中点轨迹方程.
作业21答案:1、D 2、A 3、C 4、C 5、![]() 6、
6、![]()
7、[-1,1]![]() 8、1. 2.5小时
8、1. 2.5小时
9、解:∵f(x)是偶函数,∴f(x)=f(x) ∴f(1-m)<f(m)
∵f(x)在[0,2]上是减函数,
![]() 1-m>m
1-m>m
∴ -2≤1-m≤2 解得:-1≤m<![]()
-2≤m≤2
10、解:(1) 如图建立平面直角坐标系;![]()
设Q![]() , 因为Q点在AP的中垂线上,
, 因为Q点在AP的中垂线上,
即![]() , 根据抛物线的定义知Q点的
, 根据抛物线的定义知Q点的
轨迹为抛物线.多或少设![]() ,
,![]()
所以Q点的轨迹方程为![]() .………(2分)
.………(2分)
(2)
①若k不存在, 则设MN所在的直线方程为:![]()
![]() 有
有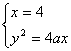
![]()
![]()
![]() ,
,![]() .
.
![]()
![]()
![]()
![]()
![]() ………(3分)
………(3分)
②若k存在, 则设MN所在的直线方程为: ![]()
![]() 有
有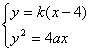
![]() ………(4分)
………(4分)
![]() ,
, ![]() ………(6分)
………(6分)
由![]()
![]()
![]()
![]()
![]()
![]()
![]() ………(7分)
………(7分)
![]() 或
或![]()
![]()
![]() ………(8分)
………(8分)
(3)
设MN的中点为T![]() ,
, ![]() ………(9分)
………(9分)
![]() ……①
……① ![]() ……②………(11分)
……②………(11分)
由①,②消去k得: ![]() 即为所求的轨迹方程. ………(12分)
即为所求的轨迹方程. ………(12分)
