高三文科复习作业（24）

班级　　 姓名　　 座号　　

 

1、直线的位置关系是　　 （　 ）

　　　 A．相离　　　　　　　　　 B．相切　　　　　　　　　 C．相交　　　　　　　　　 D．以上都有可能

2、已知函数图象与直线y=1的交点中，距离最近两点间的距离为，那么此函数的周期是　　（　 ）

A．　　　　　　　　　　　　　　 B．π　　　　　　　　　　 C．2π　　　　　　　　　　　D．4π

3、过抛物线y²=4x的焦点作直线交抛物线于A（x₁,y₁）、B（x₂,y₂）两点，如果x₁+x₂=6，则AB的长是　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　　　 A．10　　　　　　　　　　　B．8　　　　　　　　　　　　C．6　　　　　　　　　　　　D．4

4、A、B两点之间有5条网线并联，它们能通过的最大信息量分别为1，1，2，2，3，4，现从中任取三条网线且使这三条网线通过最大信息量的和大于等于7的方法共有（　 ）

　　　 A．4种　　　　　　　　　　B．5种　　　　　　　　C．6种　　　　　　　　　　　 D．7种

5、已知向量、的夹角为45°，且=4，（，则=　　　；

在方向上的投影等于　　　　　　

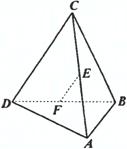
6、如图所示，在四面体ABCD中，E、F分别是AC

与BD的中点，若CD=2AB=4，EF⊥AB，则EF与CD

所成的角的大小为　　　　　　 　

7、如图，一个粒子在第一象限运动，在第一秒内，

它从原点运动到（0，1），接着它按如图所示的

轴、轴的平行方向来回运动，（即（0，0）

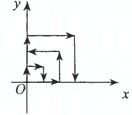→（0，1）→（1，1）→（1，0）→（2，0）

→……），且每秒移动一个单位，那么粒子运

动到（3，0）点时经过了　　　　  秒；2000秒

时这个粒子所处的位置为　　　　　　 

8、函数是奇函数，且在[－1，1]上单调递增，又上的最

大值为　　　　　  ，又若对所有的都成立，则t的取值范围是　　　　　　　　　　 . ．

9、某学校的生物实验室里有一个鱼缸，里面有6条鱼，其中4条黑色的和2条红色的，有

位生物老师每周4天有课，每天上、下各一节课，每节课前从鱼缸中任取1条鱼在课上用，用后再放回鱼缸.

　 （1）求这位生物老师在一天中上、下午所捞的鱼为同色的概率；

　 （2）求这位生物老师一周中恰有两天上、下午所捞得的鱼为不同色的概率.

10、过椭圆的右焦点F作直线l交椭圆于M、N两点，设

　 （Ⅰ）求直线l的斜率k；

　 （Ⅱ）设M、N在椭圆右准线上的射影分别为M₁、N₁，求的值.

作业（24）答案：1、B2、B3、B4、B5、，16、 7、15，（24，44）.8、1，

9、解：（1）设一天同为黑色鱼的概率为p₁，同为红色鱼的概率为p₂，

则　………………5分

答：这位生物老师在一天中上、下午所捞的鱼为同色的概率为……6分

　 （2）恰有两天不同色的概率为  ………11分

答：这位生物老师一周中恰有两天上、下午所捞得的鱼为不同的概率……12分

10、解：（Ⅰ）F（）　l：　…………2分

由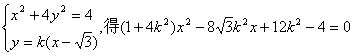　…………4分

设M　①

　　　　　　　　　　　   ②

 ③

把①②代入③，并整理，得

解得　　…………6分

（Ⅱ）设的夹角为

则由（Ⅰ）知　 ∴

∴……12分