2006高三第二次模拟试卷
数　 学

一、选择题（本题每小题5分，共60分）

1、若P={},Q=,则必有

A、PQ=　　 B、PQ　　 C、P=Q　　D、PQ

2、函数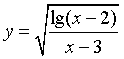的定义域是

A、　　B、　

C、　　　　　 D、

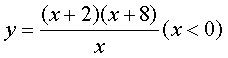3、的值域是

A、[18，+　　　　B、(-，2　　

C、[ 2，18]　　　　  D、(-，2[18，+

4、不等式 成立的一个必要不充分条件是

A、或x>1　　　　  B、x<-1或0<x<1　

C、x>1　　　　　　　　　　　　 D、x>-1

5、若

A、关于直线y=x对称　 B、关于x轴对称

C、关于y轴对称　　　　　 　　　　  D、关于原点对称

6、函数f(x)是定义域为R的偶函数，又f(x)=f(x-2),如果f(x)在[-1，0]上是减函数，那么f(x)在[2，3]上是

　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A、增函数　 B、减函数　C、先增后减的函数　 D、先减后增的函数

7、若函数f(x)=x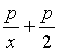－在（1，+∞）上是增函数，则实数p的取值范围是

A、［－1,＋∞　　　　  　 B、［1,+∞ 　

Ｃ、－∞,－1］　　　　　Ｄ、 －∞,1］

8、函数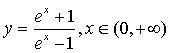的反函数是

A、　　　　 B、

C、　　 　　　 D、

9、函数=的递增递减区间分别为

A、与　　 B、与　

C、与　 D、与

10、设函数 + b+ c 给出下列四个命题：

①c = 0时，y是奇函数 　　　②b0 , c >0时，方程0 只有一个实根　 ③y的图象关于(0 , c)对称　　 　④方程0至多两个实根

其中正确的命题是

A、①、④　　　　　　　  B、①、③ 　

C、①、②、③　　　　　  D、①、②、④

11、利用数学归纳法证明“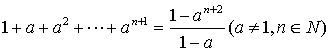”时，在验证n=1成立时，左边应该是

A、1　　　 B、　　C、　　D、

12、同一天内，甲地下雨的概率是0.15，乙地下雨的概率是0.12，假定在这天两地是否下雨相互之间没有影响，那么甲、乙两地都不下雨的概率是

A、0.102　　 B、0.132　　C、0.748　　D、0.982

　　　　　　　　　　　　　　　　　　　 二、填空题（t本题每小题4分，共16分x）

13、如果复数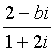（其中为虚数单位，为实数）的实部和虚部是互为相反数，那么 等于________

14、已知函数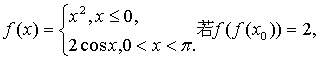则x₀=　　　　

15、若对于任意a[－1,1], 函数f(x) = x+ (a－4)x + 4－2a的值恒大于零,　则x的取值范围是　　　　 　　　　　　　　　.

16、如果函数f(x)的定义域为R，对于是不大于5的正整数，当x>－1时，f(x)>0. 那么具有这种性质的函数f(x)=　　　　  .（注：填上你认为正确的一个函数即可）

三、解答题（本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤）：

17、画出的图象，并利用此图象判定方程有两个不同实数解时，实数所满足的条件。（本题满分12分）

18、（本题满分12分）

二次函数f（x）满足若f（x）= 0有两个实数根

（1）求正数c的取值范围;　　　 （2）求的取值范围。

19、（本题满分12分）

已知集合A＝，B＝.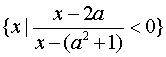

 （1）当a＝2时，求AB；　　　（2）求使BA的实数a的取值范围.

20、（本小题满分12分）设函数(a为实数).

（1）若a<0,用函数单调性定义证明:在上是增函数;

（2）若a=0,的图象与的图象关于直线y=x对称,求函的解析式.

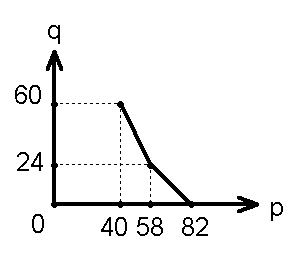
21、（本题满分12分）设f（x）是定义域是R，且对一切实数x满足f(x+2)=f(2-x),

f(x+1)=f(13-x),

（1）若f(5)=9,求f(-5);

（2）已知时，求当时，函数g(x)=2x-f(x)的表达式，并求出g(x)的最大值和最小值；

（3）若f(x)=0的一根是0，记f(x)=0在区间[-1000，1000]上的根数为N，求N的最小值。

22、某公司为帮助尚有26.8万元无息贷款没有偿还的残疾人商店，借出20万元将该商店改建为经营状况良好的某种消费品专卖店，并约定用该店经营的利润逐步偿还债务（不计息）。已知：该种消费品的进价为每件40元；该店每月销售量q（百件）与销售价p（元/件）的关系用图中的一条折线表示；职工每人每月工资为600元，该店应交付的其他费用为每月13200元。

（1）若当销售价p为52元/件时，该店正好收支平衡，求该店的职工人数。

（2）若该店只安排40名职工，则该店最早可在几年后还清所有债务，此时每件消费品价格定为多少元？

参 考 答 案

（一）

一、选择题（每小题5分，共60分）：

ADBDC，AADDC，CC

二、填空题（t每小题4分，共16分x）

(13).  (14).  (15). (-∞‚1)∪(3,+∞) ；(16).x+6或2x+6或3x+6或4x+6或5x+6

17、解：

当过时，

当直线与的图像相切时，由得x=0。

∴切点(0,1)

∴a=1-0=1

∴有两个不同实数解时，

18、解：

(1)∵f(x)=0有两个不等实数根

　∴△＞0

　即1-4C＞0　∴

(2)∵

　∵ =　=

∵∴

19. 解：（1）当a＝2时，A＝（2，7），B＝（4，5）∴ AB＝（4，5）.

（2）∵ B＝（2a，a²＋1），

当a＜时，A＝（3a＋1，2）要使BA，必须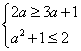，此时a＝－1；

当a＝时，A＝，使BA的a不存在；

当a＞时，A＝（2，3a＋1）

要使BA，必须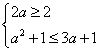，此时1≤a≤3.

综上可知，使BA的实数a的取值范围为[1，3]∪{－1}

20．解： (1)设任意实数x₁<x₂,则

f(x₁)- f(x₂)=

==　

　　　　.

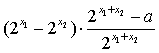
　　　　又,∴f(x₁)- f(x₂)<0,所以f(x)是增函数.

　　 (2)当a=0时,y=f(x)=2^x-1,∴2^x=y+1, ∴x=log₂(y+1),

　　　　  y=g(x)= log₂(x+1).

21、解

(1)　  由f(x+2)= f(2-x)及f(x+1)= f(13-x)得：f(x)的图像关于直线x=2,x=7对称。

∴f(x)= f(4-x)，f(x)= f(14-x)

得 f(x) = f(x+10)

∴f(x)是以10为周期的周期函数。

∴f(-5)= f(-5+10)= f(5)=9

(2)当x∈[16，17]，x-10∈[6,7]

∴f(x)= f(x-10)=(x-10-2)²=(x-12)²

当x∈(17,20),x-20∈(-3，0)，4-(x-20)∈[4,7]

∴f(x)= f(x-20)= f[4-(x-20)]

　　 = f(24-x)=(x-22)²

∴

∵x∈[16,17]，g(x)最大值为16，最小值为9；x∈(17，20),g(x)＞g(17)=9,g(x)≤g(20)=36

∴g(x)最大值为36，最小值为9。

(3)由f(0)=0,及f(0)=f(4)=0，知f(0)在[0，10]上至少有两个解。

而在[-1000，1000]上有200个周期，至少有400个解。又f（1000）=0

所以最少有401个解。且这401个解的和为1000。

22解：

（1）

设职工人数为x人，依题意：

[-2×52+140]×100×（52-40）=600x+13200

得x=50

∴该店职工数为50人。

（2）设每件消费品价格定为x元时，债务能最快还清

当x∈[40,58]，利润g₁=(x-40)(-2x+140)×100

当且仅当时，g₁的最大值是45000元

当x∈[58，82]的，利润g₂=(x-40)(-x+82)×100

当且仅当x=61时，y₂的最小值是44100元

从上分析可知，消费品定价为55元/件时，可获最大利润，债务才能最快还清