苏州中学06届高三数学冲刺训练(五)
班级![]() 姓名
姓名![]() 得分
得分![]()
一、选择题:
[ ]1已知:![]() 是R上的增函数,点
是R上的增函数,点![]() 、
、![]() 在它的图像上,
在它的图像上,![]() 为其反函数,则不等式
为其反函数,则不等式![]() <1的解集是
<1的解集是
(A)![]() ;
(B)
;
(B)![]() ; (C)
; (C)![]() ;
(D)
;
(D)![]() 。
。
[ ]2定义在R上的函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() 的最小值是(A)
的最小值是(A)![]() ;(B)
;(B)![]() ;(C)
;(C)![]() ;(D)
;(D)![]() 。
。
[ ]3设曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,则
,则
(A)![]() ;(B)
;(B)![]() ;(C)
;(C)![]() ;(D)
;(D)![]() 。
。
[ ]4已知数列![]() 、
、![]() 、
、![]() 、……、
、……、![]() 、……,它的前n项积大于
、……,它的前n项积大于![]() ,则正整数n的最小值为
(A)8; (B)10; (C)11; (D)12。
,则正整数n的最小值为
(A)8; (B)10; (C)11; (D)12。
[ ]5集合![]() ,
,![]() ,若
,若![]() 只有一个子集,则实数k的取值范围为
只有一个子集,则实数k的取值范围为
(A)![]() ; (B)
; (B)![]()
![]() ; (C)
; (C)![]() ; (D)
; (D)![]() 。
。
[ ]6有4位学生参加某种竞赛,竞赛规则规定:每位同学必须从甲、乙两题中任选一题作答,选甲答对得100分,答错得![]() 分;选乙答对得90分,答错得
分;选乙答对得90分,答错得![]() 分。若4位同学的总分为0分,则这4位同学不同得分情况的种数是
分。若4位同学的总分为0分,则这4位同学不同得分情况的种数是
(A)48; (B)36; (C)24; (D)18。
[ ]7某班有48名学生,某次数学测验,算术平均分为70分,标准差为![]() ,后发现成绩记录有误,某甲得80分却记为50分,某乙得70分却记为100分,更正后计算得标准差为
,后发现成绩记录有误,某甲得80分却记为50分,某乙得70分却记为100分,更正后计算得标准差为![]() ,则
,则![]() 与
与![]() 之间大小关系是
之间大小关系是
(A)![]() >
>![]() ; (B)
; (B)![]()
![]()
![]() ;
(C)
;
(C)![]() >
>![]()
![]() ; (D)
; (D)![]() <
<![]() 。
。
[ ]8四棱锥![]() 中,
中,![]() ,
,![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,满足上述条件的四棱锥
,满足上述条件的四棱锥![]() 的顶点
的顶点![]() 的轨迹是
的轨迹是
(A)圆; (B)不完整的圆; (C)抛物线; (D)抛物线的一部分。
[ ]9已知实数![]() 且
且![]() ,则
,则![]() 的取值范围为
的取值范围为
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ;
(D)
;
(D)![]() 。
。
[ ]10 若![]() ,则
,则![]() 的最小值为
的最小值为
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() 。
。
二、填空题:
11已知曲线![]() ,则过点
,则过点![]() 的切线方程为
的切线方程为![]() ;已知曲线
;已知曲线![]() ,则过点
,则过点![]() 的切线方程为
的切线方程为![]() 。
。
12若![]() ,则
,则![]() 的最小值等于
的最小值等于![]() 。
。
13设![]() ,若
,若![]() 的图像向左平移至少
的图像向左平移至少![]() 个长度单位后得到的图像恰为奇函数的图像,而向右平移至少
个长度单位后得到的图像恰为奇函数的图像,而向右平移至少![]() 个长度单位后得到的图像恰为偶函数的图像,则
个长度单位后得到的图像恰为偶函数的图像,则![]() 的最小正周期为
的最小正周期为![]() 。
。
14将一个侧棱互不相等的四棱锥![]() 的每个顶点染上一种颜色,并使同一条棱的两个端点异色,如果只有5种颜色可供,那么不同的染色方法种数为
的每个顶点染上一种颜色,并使同一条棱的两个端点异色,如果只有5种颜色可供,那么不同的染色方法种数为![]() 。
。
15给出命题:①圆![]() 关于点
关于点![]() 对称的圆方程为
对称的圆方程为![]() ;②双曲线
;②双曲线![]() 右支上一点P到左准线距离为18,则该点到右焦点距离为
右支上一点P到左准线距离为18,则该点到右焦点距离为![]() ;③顶点在原点,对称轴为坐标轴,且过
;③顶点在原点,对称轴为坐标轴,且过![]() 的抛物线方程只能是
的抛物线方程只能是![]() ;④
;④![]() 、
、![]() 是椭圆
是椭圆![]() 上两个动点,
上两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 、
、![]() 的斜率之积为
的斜率之积为![]() ,则
,则![]() 等于定值20。把你认为正确的命题序号填写在横线上
等于定值20。把你认为正确的命题序号填写在横线上![]() 。
。
16已知椭圆的离心率为![]() ,
,![]() 、
、![]() 是两个焦点,
是两个焦点,![]() 是椭圆上任意一点,则
是椭圆上任意一点,则![]() 的最大值为
的最大值为![]() 。
。
三、解答题:
17 甲、乙两公司生产同一种产品,经测算,对于函数![]() 、
、![]() 及任意的
及任意的![]() ,当甲公司投入
,当甲公司投入![]() 万元作宣传时,若乙公司投入的宣传费小于
万元作宣传时,若乙公司投入的宣传费小于![]() 万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入
万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入![]() 万元作宣传时,若甲公司投入的宣传费小于
万元作宣传时,若甲公司投入的宣传费小于![]() 万元,则甲公司有失败的风险,否则无失败风险。
万元,则甲公司有失败的风险,否则无失败风险。
(Ⅰ)试解释![]() 、
、![]() 的实际意义;(Ⅱ)当
的实际意义;(Ⅱ)当![]() ,
,![]() 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用。问此时甲、乙两公司各应投入多少宣传费?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用。问此时甲、乙两公司各应投入多少宣传费?
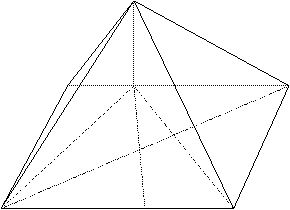 18 如图,四棱锥
18 如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 平面
平面![]() ,垂足为
,垂足为![]() ,
,![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 的中点,四面体
的中点,四面体![]() 的体积是
的体积是![]() 。
P
。
P
(Ⅰ)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离;
A
G
D
的距离;
A
G
D
(Ⅲ)若点![]() 是棱
是棱![]() 上一点且
上一点且![]() ,
,
求![]() 的值。
的值。
B E C
19已知数列![]() 与
与![]() 满足关系:
满足关系:![]() ,
,![]() ,
,![]()
(a>0)。
(Ⅰ)求数列![]() 的通项公式并证明:
的通项公式并证明:![]() ;(Ⅱ)设
;(Ⅱ)设![]() 是数列
是数列![]() 的前n项的和,当
的前n项的和,当![]() 时
时![]() 与
与![]() 是否有确定的大小关系?若有则加以证明;若没有则说明理由。
是否有确定的大小关系?若有则加以证明;若没有则说明理由。
20从原点出发的某质点M,按照向量![]() 移动的概率为
移动的概率为![]() ,按照向量
,按照向量![]() 移动的概率为
移动的概率为![]() ,设M可到达点
,设M可到达点![]() 的概率为
的概率为![]() 。
。
(Ⅰ)求![]() 、
、![]() ; (Ⅱ)求证:
; (Ⅱ)求证:![]() ;
(Ⅲ)求
;
(Ⅲ)求![]() 的表达式。
的表达式。
21已知点![]() 在椭圆
在椭圆![]() (a>b>0)的第一象限上运动。
(a>b>0)的第一象限上运动。
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;(Ⅱ)若把轨迹
的方程;(Ⅱ)若把轨迹![]() 的方程表达式记为:
的方程表达式记为:![]() ,且在区间
,且在区间![]() 内
内![]() 有最大值,试求椭圆
有最大值,试求椭圆![]() 的离心率的取值范围。
的离心率的取值范围。
苏州中学06届高三数学冲刺训练(五)参考答案
1B2A3D4C5B6B7D8B9A10C
11、![]() ;
;![]() 及
及![]() ;12、
;12、![]() ;13、2π;14、420;
;13、2π;14、420;
15、②④ ;16、![]() 。
。
解17①:![]() 表示当甲公司不投入宣传费时,乙公司要回避失败的风险至少要投入11万元的宣传费;
表示当甲公司不投入宣传费时,乙公司要回避失败的风险至少要投入11万元的宣传费;![]() 表示当乙公司不投入宣传费时,甲公司要回避失败的风险至少要投入21万元的宣传费。
表示当乙公司不投入宣传费时,甲公司要回避失败的风险至少要投入21万元的宣传费。
②设甲、乙公司投入的宣传费分别为x、y万元,当且仅当![]() ……①,
……①,
![]() ……②时双方均无失败的风险,由①②得
……②时双方均无失败的风险,由①②得![]() 易解得
易解得
![]() ,所以
,所以![]() ,故
,故![]() 。
。
解18:
解19:①∵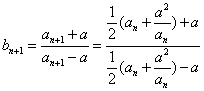
![]() >0,∴
>0,∴![]()
![]() ,又
,又![]() ,∴
,∴![]() ,所以
,所以![]() ,
,![]() ,
,
∴![]() 。
。
②当![]() 时
时![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号)
∴![]() ,
,![]() <
<![]() ……,
……,![]() <
<![]() ,
,
∴![]() <
<![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() <
<![]() ,
,
∴![]() <
<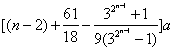 <
<![]() <
<![]() 。
。
解20:①点M到达点![]() 的概率
的概率![]() 。
。
点M到达点![]() 的事件由两个互斥的事件组成:点M先按向量
的事件由两个互斥的事件组成:点M先按向量![]() 移动到达点(0,1),再按向量
移动到达点(0,1),再按向量![]() 平移动到达点(0,2),此时概率为
平移动到达点(0,2),此时概率为![]() ;点M按向量
;点M按向量![]() 移动直接到达点(0,2),此时概率为
移动直接到达点(0,2),此时概率为![]() 。故所求概率
。故所求概率![]()
![]() ;
;
②点M到达点![]() 的事件由两个互斥的事件组成:从点
的事件由两个互斥的事件组成:从点![]() 按向量
按向量![]() 移动,此时概率为
移动,此时概率为![]() ;从点(0,n)按向量
;从点(0,n)按向量![]() 移动,此时概率为
移动,此时概率为![]() 。于是
。于是
![]() 即
即![]() ;
;
③由②可知数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,即
为公比的等比数列,即![]() 故
故![]() 。
。
![]()
![]()
解21:①椭圆![]() (a>b>0)的参数方程为
(a>b>0)的参数方程为 ![]() (θ为参数)
(θ为参数)
![]() 又设点
又设点![]() 是轨迹
是轨迹![]() 上任意一点,则
上任意一点,则 ![]()
![]() (θ为参数)
(θ为参数)
消去参数θ得![]() ,故轨迹
,故轨迹![]() 的方程
的方程![]() 。
。
②把方程![]() 表达为函数解析式为:
表达为函数解析式为:![]() ,可证函数在
,可证函数在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,因此函数在
上为减函数,因此函数在![]() 上有最大值且在
上有最大值且在![]() 处取得最大值,要使函数在
处取得最大值,要使函数在![]() 内取到最大值,则只要
内取到最大值,则只要![]() <
<![]() 即
即![]() <
<![]() ,从而
,从而![]() <
<![]() <1。
<1。
