2006年高考猜题试卷
【试题1】某地区在高三第二轮复习组织一次大型调研考试,考试后统计的数学成绩服从正态分布,其密度函数![]() ,则下列命题不正确的是
,则下列命题不正确的是
A. 某地区这次考试的数学平均数为88分
B.分数在120分以上的人数与分数在56分以下的人数相同
C. 分数在120分以上的人数与分数在60分以下的人数相同
D. 某地区这次考试的数学标准差为10
【猜题理由】正态分布在新课标中,只要求它的基本性质,特别是正态曲线的对称性,而这些在现在高考命题是可操作的.
【解答】由题意可知,μ=88,σ2=100,∴σ=10,由正态分布曲线的对称性可知仅C不正确.故选C.
【试题2】三棱锥P-ABC中,顶点P在平面ABC的射影为O满足![]() +
+![]() +
+![]() =0,A点在侧面PBC上的射影H是△PBC的垂心,PA=6,则此三棱锥体积最大值是
=0,A点在侧面PBC上的射影H是△PBC的垂心,PA=6,则此三棱锥体积最大值是
A.36 B.48 C.54 D.72
【猜题理由】动态几何问题能有效地考查考生的能力,而且本题利用向量这一工具,使三棱锥体积最大值问题顺利地解决,具有较强的综合性.
 【解答】∵
【解答】∵![]() +
+![]() +
+![]() =0,∴O为⊿ABC的重心.又A点在侧面PBC上的射影H是△PBC的垂心,∴PH⊥BC,而PA在侧面PBC上的射影为PH,∴PA⊥BC,又而PA在面ABC上的射影为PO,∴AO⊥BC. 同理可得CO⊥AB,∴O是△ABC的垂心. 由于⊿ABC的重心与垂心重合,所以⊿ABC为等比三角形,即三棱锥P-ABC为正三棱锥. 设AB=x,则AO=,∴PO=,∴V= ×x2×= ,令f(x)=108x4―x6,则f(x)=6x3(72―x2),∴当x∈(0,6)时f(x)递增;当x∈(6,6)时f(x)递减,故x=6时f(x)取得最大值36. 故选A.
=0,∴O为⊿ABC的重心.又A点在侧面PBC上的射影H是△PBC的垂心,∴PH⊥BC,而PA在侧面PBC上的射影为PH,∴PA⊥BC,又而PA在面ABC上的射影为PO,∴AO⊥BC. 同理可得CO⊥AB,∴O是△ABC的垂心. 由于⊿ABC的重心与垂心重合,所以⊿ABC为等比三角形,即三棱锥P-ABC为正三棱锥. 设AB=x,则AO=,∴PO=,∴V= ×x2×= ,令f(x)=108x4―x6,则f(x)=6x3(72―x2),∴当x∈(0,6)时f(x)递增;当x∈(6,6)时f(x)递减,故x=6时f(x)取得最大值36. 故选A.
【试题3】若关于的方程x2―(a2+b2―6b)x+ a2+b2+2a―4b+1=0的两个实数根x1,x2满足x1≤0≤x2≤1,则a2+b2+4a的最大值和最小值分别为
 A.和5+4
B. ―和5+4 C. ―和12
D. ―和15―4
A.和5+4
B. ―和5+4 C. ―和12
D. ―和15―4
【猜题理由】本题在函数、方程、线性规划的交汇处命题,有效地考查了函数与方程思想方法,以及解答线性规划的基本方法.
【解答】令f(x)= x2―(a2+b2―6b)x+ a2+b2+2a―4b+1,则由题意有f(0)= a2+b2+2a―6b+1≤0且f(1)=2a+2b+2≥0,即(a+1)2+(b―2)2≤4且a+b+1≥0,在直角坐标平面aOb上作出其可行域如图所示,而a2+b2+4a=(a+2)2+b2―4的几何意义为PA2―4(其中P(a,b)为可行域内任意的一点,A(―2,0)). 由图可知,当P点在直线l:a+b+1=0上且AP⊥l时取得最小值;当P点为AC(C为圆(a+1)2+(b―2)2≤4的圆心)的延长线与圆C的交点时达到最大值. 又A点的直线l的距离为,AC=,所以a2+b2+4a的最大值和最小值分别为―和(+2)2―4=5+4.故选B.
【试题4】已知函数f(x)=x3+ax2+bx+c的图象经过原点,且在x=1处取得极值,直线y=2x+3到曲线y=f(x)在原点处的切线所成的夹角为450.
(1)求f(x)的解析式;
(2)若对于任意实数α和β恒有不等式 f(2sinα)―f(2sinβ)≤m成立,求m的最小值
(3)若g(x)=xf(x)+tx2+kx+s,是否存在常数t和k,使得对于任意实数s,g(x)在[-3,―2]上递减,而在[-1,0]上递增,且存在x0(x0>1)使得g(x)在[1,x0]上递减?若存在,求出t+ k的取值范围;若不存在,则说明理由.
【猜题理由】本题在函数和导数、以及线性规划的交汇处命题,具有较强的预测性,而且设问的方式具有较大的开放度,情景新颖.
【解答】(1)由题意有f(0)= c=0,f(x)=3 x2+2ax+b,且f(1)= 3+2a+b=0.
又曲线y=f(x)在原点处的切线的斜率k=f(0)= b,而直线y=2x+3到它所成的夹角为450,
∴1=tan450= ,解得b=― 3. 代入3+2a+b=0得a=0.
故f(x)的解析式为f(x)=x3― 3x.
(2)∵对于任意实数α和β有2sinα,2sinβ∈[-2,2].
由f(x)=3x2―3=3(x―1) (x+1)可知,f(x)在(-∞,―1]和[1,+∞)上递增;在[-1,1]递减.
又f(―2)= ―2,f(―1)= 2,f(1)= ―2,f(2)= 2,
∴f(x)在[-2,2]上的最大值和最小值分别为―2和2.
∴对于任意实数α和β恒有 f(2sinα)―f(2sinβ)≤4.
故m≥4,即m的最小值为4.
(3)∵g(x)=x(x3― 3x)+tx2+kx+s= x4+(t―3)x2+kx+s,∴g(x)= 4 x3+2(t―3)x+k,
∴要使g(x)在[-3,―2]上递减,而在[-1,0]上递增,且存在x0(x0>1)使得g(x)在[1,x0]上递减,只需在[-3,―2]和[1,x0]上g(x)≤0,而在[-1,0]上g(x)≥0.
令h(x)= g(x),则h(x)= 12 x2+2(t―3),当t―3≥0时,h(x)在R上恒为非负,此时显然不存在这样的常数t和k,∴t―3<0.
当t―3<0时,g(x)在(-∞,―]和[,+∞)上递增,而在[―,―]上递减.
∴要使h(x)在[-3,―2]和[1,x0]上h(x)≤0,而在[-1,0]上h(x)≥0,只需h(―2)= ―32 ―4 (t―3)+k

即
作出可行域如图所示,由图可知,当直线t+ k= z过A点时z取得最大值5,当直线t+ k= z过B点时z取得最大值―5.
故存在这样的常数t和k,其取值范围为[-5, 5].
【试题5】 “建设创新型国家”是2006年3月份召开的“两会”(全国人大、政协)的主要议题. 某公司为了响应党中央的号召,决定投资创新科技的研发,经调查有两个可投资意向的项目:A项目是国家重点扶持尖端型创新科技研发的项目,每年需要研发的经费5a万元,若能申请国家扶持成功,则在近三年内每年可得到国家的研发经费a万元,在研发的第n年能研发成功的概率组成以2为公比、0.01为首项的等比数列,2010年后将失去研发价值,若能研发成功在2026年以前(包括2026年)每年(从研发成功的第二年起)将获得经济效益10a万元;B项目是该公司的垄断的基础型创新研发的项目,每年需要研发的经费2a万元,在当年内能研发成功的概率组成以0.1为公差、0.1为首项的等差数列,估计3年后将失去研发价值,若能研发成功在2015年(包括2015年)以前每年(从研发成功的第二年起)将获得经济效益3a万元. 并且项目研发上马后就不会在中途停止研发,直到没有研发价值的时候为止.在全国范围内另外有1个像该公司具有研发A项目实力的公司准备在2006年投资研发A项目,若在某一年有几个公司同时研发成功,则以后A项目的所有的经济效益由同时研发成功的这几个公司均分. 请你帮助该公司作出决策:在2006年应该投资研发哪一个项目?并说明你的理由.
【猜题理由】本题取材于社会热点问题,情景新颖,背景公平,具有较好的教育意义,而且能较好地考查考生灵活地运用所学的概率知识来分析解决实际问题的能力,体现了新课标的理念.
【解答】(1)若该公司投资研发A项目,则:若该公司在2006年研发成功,其经济效益期望为Eξ11=200a ×0.01×(1―0.01)+100a ×0.01×0.01≈1.99a万元.
若该公司在2006年没有研发成功,而另一个公司在2006年研发成功,于是该公司的经济效益期望为Eξ12=―4a ×(1―0.01)×0.01≈―0.0396a万元.
若该公司在2007年研发成功,其经济效益期望为
Eξ21=190a ×0.02×(1―0.02)+a ×0.02×0.02≈3.762a万元.
若该公司在2007年没有研发成功,而另一个公司在2007年研发成功,于是该公司的经济效益期望为Eξ22=―8a ×(1―0.02)×0.02≈―0.0784a万元.
若该公司在2008年研发成功,其经济效益期望为
Eξ31=180a ×0.04×(1―0.04) +a ×0.04×0.04≈7.056a万元.
若该公司在2008年没有研发成功,而另一个公司在2008年研发成功,于是该公司的经济效益期望为Eξ32=―12a ×(1―0.04)×0.04 ≈―0.1536a万元.
若该公司在2009年研发成功,其经济效益期望为
Eξ41=170a ×0.08×(1―0.08)+a ×0.08×0.08≈13.056a万元.
若该公司在2009年没有研发成功,而另一个公司在2009年研发成功,于是该公司的经济效益期望为Eξ42=―17a ×(1―0.08)×0.08≈―0.2944a万元.
若该公司在2010年研发成功,其经济效益期望为
Eξ51=160a ×0.16×(1―0. 16)+a ×0. 16×0. 16≈23.552a万元.
若该公司在2010年没有研发成功,则该公司总要损失22 a万元,于是该公司的经济效益期望为Eξ52=―22a ×(1―0. 01―0. 02―0. 04―0. 08―0. 16)≈―15.18a万元.
所以该公司投资研发A项目的经济效益期望为Eξ11+ Eξ12+ Eξ21+ Eξ22+ Eξ31+ Eξ32+ Eξ41+ Eξ42+ Eξ51+ Eξ52≈33.67 a万元.
其投资的期望为4a[0.01+(1―0.01)×0.01]+ 8a[0.02+(1―0.02)×0.02]+ 12a[0.04+(1―0.04)×0.04]+ 17a[0.08+(1―0.08)×0.08]+ 22a{1―[0.01+(1―0.01)×0.01]―[0.02+(1―0.02)×0.02]―[0.04+(1―0.04)×0.04]―[0.08+(1―0.08)×0.08]=19.5354 a
其投资的经济效益期望的平均效率为≈1.723538,平均每年的经济效益期望为≈11.22333万元.
(2)设该公司投资研发B项目的经济效益为η万元,则ξ的可能取值为27a,24a,21a,―6a. 而P(η=27a)= 0. 1,P(η=24a)= 0. 2,P(η=21a)= 0. 3, P(η=―6a)= 0. 7,
∴Eη=27a×0.1+24a×0.2+21a×0.3―6a×0.3=12 a万元.
其投资的期望为2a×0. 1+ 4a×0.2+ 6a×0.7=5.2 a万元.
其投资的经济效益期望的平均效率为2.,平均每年的经济效益期望为4a万元.
尽管A项目的投资经济效益期望的平均效率比B项目略低,但总的经济效益期望和平均每年的经济效益期望比B项目高得多,故应建议该公司在2006年投资研发A项目.
【试题6】在直角坐标平面中,ΔABC的两个顶点AB的坐标分别为A(―a,0),B(a,0)(a>0),两动点M,N满足![]() +
+![]() +
+![]() =0,
=0,![]() =
=![]() =
=![]() ,向量
,向量![]() 与
与![]() 共线.
共线.
(1)求ΔABC的顶点C的轨迹方程;
(2)若过点P(0,a)的直线与(1)
轨迹相交于E、F两点,求![]() ·
·![]() 的取值范围;
的取值范围;
(3)(理科作)若G(―a,0),H(2a,0),Q点为C点轨迹在第一象限内的任意一点,则是否存在常数λ(λ>0),使得∠QHG=λ∠QGH 恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【猜题理由】本题本题在平面向量和解析几何的交汇处命题,重点考查了解析几何的基本思想方法,体现最新《考试大纲》的要“构造有一定的深度和广度的数学问题”高考命题要求.
【解答】(1)设(x,y),∵![]() +
+![]() +
+![]() =0,∴M点是ΔABC的重心,∴M(,).
=0,∴M点是ΔABC的重心,∴M(,).
又![]() =
=![]() 且向量
且向量![]() 与
与![]() 共线,∴N在边AB的中垂线上,∴N(0,).
共线,∴N在边AB的中垂线上,∴N(0,).
而![]() =
=![]() ,∴=,即x2― =a2.
,∴=,即x2― =a2.
(2)设E(x1,y1),F(x2,y2),过点P(0,a)的直线方程为y=kx+a,
代入x2― =a2得 (3―k2)x2―2akx―4a2=0
∴Δ=4a2k2+16a2(3―k2)>0,即k2<4. ∴k2―3<1,∴>4或<0.
而x1,x2是方程的两根,∴x1+x2=,x1x2=.
∴![]() ·
·![]() =(x1,y1―a)·(x2,y2―a)= x1x2+kx1·kx2=(1+k2) x1x2==4a2(1+)∈(-∞, 4a2)∪(20a2,+∞).
=(x1,y1―a)·(x2,y2―a)= x1x2+kx1·kx2=(1+k2) x1x2==4a2(1+)∈(-∞, 4a2)∪(20a2,+∞).
故![]() ·
·![]() 的取值范围为(-∞,4a2)∪(20a2,+∞).
的取值范围为(-∞,4a2)∪(20a2,+∞).
(3) 设Q(x0,y0) (x0>0,x0>0),则x02― =a2,即y02=3(x02―a02).
当QH⊥x轴时,x0=2a,y0=3a,∴∠QGH=,即∠QHG= 2∠QGH,故猜想λ=2,使∠QHG=λ∠QGH总成立.
当QH不垂直x轴时,tan∠QHG=―,tan∠QGH= ,
∴tan2∠QGH= = = = =―= tan∠QHG.
又2∠QGH与∠QHG同在(0,)∪(,π)内,∴2∠QGH=∠QHG.
故存在λ=2,使2∠QGH=∠QHG恒成立.
【试题7】在直角坐标平面中,过点A1(1,0)作函数f(x)=x2(x>0)的切线l1,其切点为B1(x1,y1);过点A2(x1,0)作函数g(x)=ex(x>0)的切线l2,其切点为B2(x2,y2);过点A3(x2,0)作函数f(x)= x2(x>0)的切线l3,其切点为B3(x3,y3);如此下去,即过点A2k―2(x2k―2,0)作函数f(x)=x2(x>0)的切线l2k―1,其切点为B2k―1 (x2k―1,y2k―1);过点A2k―1 (x2k―1,0)作函数g(x)= ex (x>0)的切线l2k,其切点为B2k (x2k,y2k);….
(1)探索x2k―2与x2k―1的关系,说明你的理由,并求x1的值;
(2)探索x2k―1与x2k的关系,说明你的理由,并求x2的值;
(3)求数列{xn}通项公式xn;
(4)是否存在实t,使得对于任意的自然数n和任意的实数x,不等式+ ++…+≤3tx4―4tx3―12tx2+33t―恒成立?若存在,求出这样的实数t的取值范围;若不存在,则说明理由.
【猜题理由】本题以导数为背景,命制出数列与函数、导数、不等式的综合试题,重点考查数列的基本思想方法,综合较强,与高考的压轴题的难度相当,具有较强的预测性.
【解答】(1)∵f(x)=2x,∴切线l2k―1的方程为y―x2k―12=2 x2k―1(x―x2k―1),又切线l2k―1过点A2k―2(x2k―2,0),∴0―x2k―12=2 x2k―1(x2k―2―x2k―1),且x2k―1>0,∴x2k―1=2 x2k―2.∴x1=2.
(2)又g(x)=( ex) = ex,∴切线l2k的方程为y―e![]() =e
=e![]() (x―x2k),而切线l2k过点A2k―1(x2k―1,0),∴0―e
(x―x2k),而切线l2k过点A2k―1(x2k―1,0),∴0―e![]() = e
= e![]() (x2k―1―x2k),且x2k>0,∴x2k= x2k―1+1. ∴x2=x1+1=3.
(x2k―1―x2k),且x2k>0,∴x2k= x2k―1+1. ∴x2=x1+1=3.
(3)由(1) (1)可知x2k= x2k―1+1 = 2x2k―2+1,即x2k+1= 2(x2k―2+1),∴数列{x2k +1}为等比数列,且首项为4,∴x2k +1=4×2k―1,即x2k =2k+1―1.
而x2k―1=2 x2k―2=2(2k―1)= 2k+1―2,故数列{xn}通项公式为xn=
(4) (理)令Sn= + ++…+= +++…+, ∴Sn= +++…+,
两式相减得Sn= ++++…+― = ― = (1―)―,
∴Sn=1―― =1―.
∴Sn+1― Sn=(1―)―(1― )=>0,∴数列{ Sn}递增.
又当n≥6时,2n+1=2(1+1) n=2(1+C+C+C+C+…+C+C+C+C)>4(1+C+C)>2(n2+n),∴0<<,而=0,∴Sn=1.
令h(x)= 3tx4―4tx3―12tx2+33t―,则h(x)= 12t(x3―x2―2x)= 12tx(x+1)(x―2),
∴当t<0时,h(x)在(―∞,―1)和(0,2)上递增,在(―1, 0)和(2,+∞)上递减,此时不存在这样的实数t.
当t>0时,h(x)在(―∞,―1)和(0,2)上递减,在(―1, 0)和(2,+∞)上递增,
∴h(x)在x=―1或x=2处取得极小值,而h(―1)=―5t+33t―,h(2)=―32t+33t―,
∴h(x)min= t―.
∴对于任意的自然数n和任意的实数x不等式恒成立等价于t―≥1,
 而t>0,所以有t2―t―6≥0,解得t≥3或t≤―2 (舍).
而t>0,所以有t2―t―6≥0,解得t≥3或t≤―2 (舍).
故存在这样的实数t,其取值范围为t≥3.
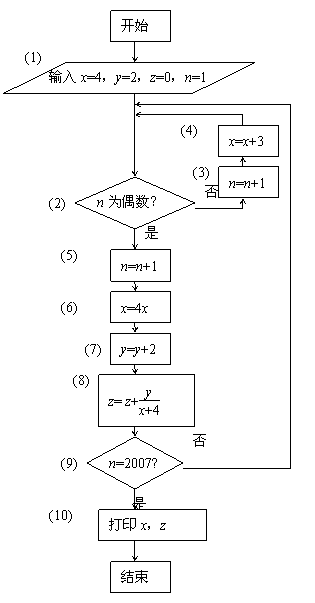
【试题8】右图是某计算机的程序框图.
(1)求打印出来的x的值;
(2)求打印出来的z的值;
(3)若将程序框图中的语句(9)“n=2007?”改为“z≥1?”,则张三同学说这是死循环(即一直无限的算下去而没有结果),而李四说不会是死循环,你认为哪个同学说的正确?并说出你的理由.
【猜题理由】本题以程序框图作背景,情景新颖,而且体现了新课标的理念,与新课标联系紧密,是新课程教材(现行教材)向新课标教材过渡时期的优秀试题.
【解答】(1)从数列角度来看,语句(4)(即“x=x+3”) 可以理解为xn+1=xn+3(其中n∈N*),语句(6)(即“x=4x”)可以理解为xn+1=4xn(其中n∈N),而语句(2)~(6)是一个小循环,执行的程序是xn+1=(k∈N). 同理语句(2)~(9)是一个大循环,其终止条件为“n=2007”.
于是问题转化为:在数列{xn}中,x1=4,xn+1=(k∈N),求x2007.
∴x2n+2= x2n+1+3=4 x2n+3,即x2n+2+1=4 x2n+4=4 (x2n+1),
令an= x2n+1,则an=1=4an,∴数列{ an}为等比数列,且a1=x2+1=(x1+3)+1==8,∴an==8×4n―1=2×4n.
故x2n=2×4n―1,∴x2n―2=2×4n―1―1,∴x2n―1=4 x2n―2=4(2×4n―1―1)= 2×4n―4.
故x2007= x2×1004―1= 2×41004―4= 22009―4,即打印出来的x的值为22009―4.
(2)由于经过语句(2)~(7)的小循环后,n为偶数才执行语句(7)(即“y=y+4”),从数列角度来看,它可以理解为y2n+1=y2n―1+2(其中n∈N*).
令bn= y2n―1,则bn+1=bn+2,数列{bn}为等差数列,且b1= y1=2,∴bn==2+2(n―1) =2 n.
∴y2n―1=2 n.
此时语句(8) (即“z= z+”)执行的程序是z2n+1= z2n―1+. 于是令cn=,则z2n―1为数列{cn}的前项和,∴z2n―1= ++…+ = ++…+,
两边同乘以得 z2n―1= ++…++,
两式相减得 z2n―1= +++…+― =+ ― =+ (1―)―= ―,∴z2n―1= ―.
故z2007=z2×1004―1=―,即打印出来的x的值为―.
(3)由于对于任意的自然数n,都有z2n―1= ―<1,即不存在自然数n,使得z2n―1≥ 1.
所以张三同学说的是对的.





1.设![]() 的定义域为
的定义域为![]() ,
,![]() 的导函数为
的导函数为![]() ,且对任意正数
,且对任意正数![]() 均有
均有![]() ,
,
(Ⅰ) 判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ) 设![]() ,
,![]()
![]() ,比较
,比较![]() 与
与![]() 的大小,并证明你的结论;
的大小,并证明你的结论;
(Ⅲ)设![]() ,
,![]() ,
,![]()
![]()
![]() ,若
,若![]() ,比较
,比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
解:(Ⅰ)由于![]() 得,
得,![]() ,而
,而![]() ,则
,则![]() ,
,
则![]()
![]() ,因此
,因此![]() 在
在![]() 上是增函数.
上是增函数.
(Ⅱ)由于![]() ,
,![]()
![]() ,则
,则![]() ,而
,而![]() 在
在![]() 上是增函数,
上是增函数,
则![]() ,即
,即![]() ,∴
,∴![]() (1),
(1),
同理 ![]() (2)
(2)
(1)+(2)得:![]() ,而
,而![]() ,
,
因此 ![]() .
.
(Ⅲ)证法1: 由于![]() ,
,![]()
![]() ,则
,则![]() ,而
,而![]() 在
在![]() 上是增函数,则
上是增函数,则![]() ,即
,即![]() ,
,
∴ ![]()
同理 ![]()
……………
![]()
以上![]() 个不等式相加得:
个不等式相加得:
![]()
而![]()
![]()
![]()
![]()
证法2:数学归纳法
(1)当![]() 时,由(Ⅱ)知,不等式成立;
时,由(Ⅱ)知,不等式成立;
(2)当![]()
![]() 时,不等式
时,不等式![]()
![]()
![]() 成立,
成立,
即![]()
![]()
![]() 成立,
成立,
则当![]() 时,
时, ![]()
![]()
![]() +
+![]()
再由(Ⅱ)的结论, ![]() +
+![]()
![]()
![]() +
+![]()
![]()
因此不等式![]()
![]()
![]() 对任意
对任意![]() 的自然数均成立.
的自然数均成立.
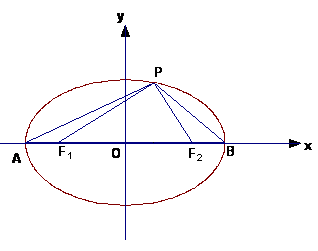 2.设椭圆
2.设椭圆![]()
![]() 的两焦点坐标分别为F1(
的两焦点坐标分别为F1(![]() 和F2
和F2![]() ,它与
,它与![]() 轴的两交点分别为A、B,点P为椭圆上一点,若F1P⊥PF2,
轴的两交点分别为A、B,点P为椭圆上一点,若F1P⊥PF2,![]() ,求椭圆方程.
,求椭圆方程.
解:由于∠F1PF2=900,则![]() ,
,
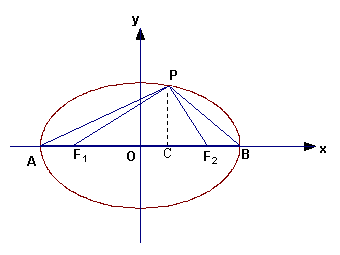 ∴
∴![]() ,设点P
,设点P![]() 在第一象限,则
在第一象限,则![]()
∴![]() ,由于
,由于![]() ,
,![]() ,
,
∴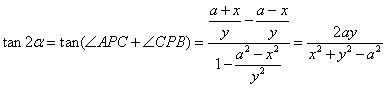
而![]() ,∴
,∴![]()

∴ ![]() ,故所求的椭圆方程为
,故所求的椭圆方程为![]() .
.
(一)设U为全集,A、B是U的两个子集,则与集合![]() 一定相等的是( )
一定相等的是( )
(A)A∩B (B)A∪B (C) ![]() (D)
(D) ![]()
(理由):摩根公式:![]()
![]()
在教材中虽未指出,但多次出现,以培养学生的发现能力、观察能力,意
在考查集合的子、交、并、补、韦恩图等概念,以及灵活的解题能力。
(详解):本小题可利用特例法或画韦恩图易得答案C。
(二)已知![]()
则有:![]()
![]()
![]()
若设:![]()
类比上例则可得到![]() 与
与![]() 的关系式为____________.(只须写出一种即可)
的关系式为____________.(只须写出一种即可)
(理由):双曲正弦函数![]()
双曲余弦函数![]()
及其性质是近几年来高考中的热点,着重考查奇偶性、反函数及图象的凸
凹性等。本题是由《全日制高中教科书》(高一数学上册)P103第6题改编
而成。考查学生的联想与类比能力。
(详解):易证:![]()
![]()
![]()
(三)(1)以椭圆的焦点弦为直径的圆必与其相应的准线相离.
(2)以双曲线的焦点弦为直径的圆必与其相应的准线相交.
(3)以抛物线的焦点弦为直径的圆必与其相应的准线相切.
(理由):本题亦可出为选择题或解答题中其中一问证明。意在考查圆锥曲线的第二
定义及判定直线与圆的位置关系等相关概念和方法。
(详解):设圆锥曲线过焦点F的弦为AB,过A、B分别向相应的准线作垂线
![]() ,则由第二定义得:
,则由第二定义得:
![]()
∴![]()
设以AB为直径的圆半径为r,圆心到准线的距离为d,即有![]()
椭圆的离心率 ![]() ,此时
,此时![]() . 相离
. 相离
抛物线的离心率 ![]() ,此时
,此时![]() . 相切
. 相切
双曲线的离心率 ![]() ,此时
,此时![]() . 相交
. 相交
(四)已知:等差数列![]() 的首项
的首项![]() ,公差
,公差![]()
(I)
设![]() .
.
(II)设![]() .
.
(理由):本题意在考查等差、等比数列求和,以及组合数的性质等有关概念。
在各章知识的交汇处命题。
第(I)问灵活利用教材中等差数列前n项和公式的推导方法——倒序相
加法。
第(II)问灵活利用教材中等比数列前n项和公式的推导方法——错位相
减法。
(详解):(I)![]()
又:![]()
两式相加得:
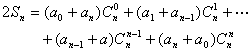
由等差数列性质知:a0 + an = a1 + an-1 = … = an + a0
∴![]()
即:![]()
(II)由![]()
![]()
∴![]()
两式相减得:
![]()
∴![]()
试题1:设![]() >0,m>0,若函数f(x)=m sin
>0,m>0,若函数f(x)=m sin![]() cos
cos![]() 在区间[-
在区间[-![]() ,
,![]() ]上单调递增,则
]上单调递增,则![]() 的范围是
B
的范围是
B
A.(0,) B.(0,) C.[ ,+∞] D.[1,+∞]
猜题理由:三角函数的图像和性质历来是高考创新试题的“试验田”,重点是对单调性与周期性的考查。该题给出了f(x)在某个区间上的单调性,求![]() 的范围,这正是该题的新颖之处。
的范围,这正是该题的新颖之处。
![]()
|
![]() ≤
≤![]()
故选B。
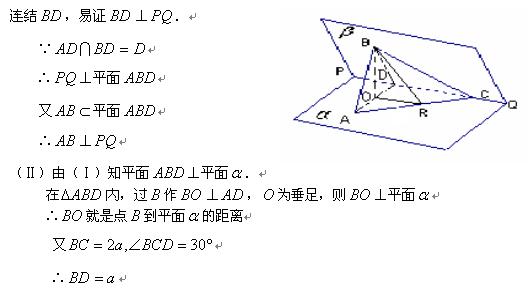
试题2:在60°的二面角![]() l-
l-![]() 中,动点A∈
中,动点A∈![]() ,动点B∈
,动点B∈![]() ,AA1
,AA1![]()
![]() ,垂足为A1,且AA1=a,AB=a,那么,点B到平面
,垂足为A1,且AA1=a,AB=a,那么,点B到平面![]() 的最大距离是
的最大距离是
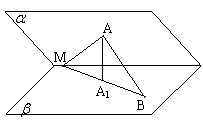 猜题理由:近十年高考立体几何试题,几乎没有涉及仅是“二面角内部”的数学问题,这类问题可以很集中的反应线面关系,更能考察学生分析问题和解决问题的能力,另外该题涉及到了浓重的平面几何问题,这正是高考对考生的新要求。
猜题理由:近十年高考立体几何试题,几乎没有涉及仅是“二面角内部”的数学问题,这类问题可以很集中的反应线面关系,更能考察学生分析问题和解决问题的能力,另外该题涉及到了浓重的平面几何问题,这正是高考对考生的新要求。
详细解答:如图:过点A做AM![]() l,垂足为M,连接
l,垂足为M,连接
|
的平面角,即![]() AMA1=60°,又AA1
AMA1=60°,又AA1![]()
![]() ,AA1=a
,AA1=a
∴AA1![]() A1B,∵AA1=a,AB=a,∴A1B=a。
A1B,∵AA1=a,AB=a,∴A1B=a。
故点B的轨迹是平面![]() 内以A1为圆心,a为半径的圆,显然B、A1、M三点共线时,点B到平面
内以A1为圆心,a为半径的圆,显然B、A1、M三点共线时,点B到平面![]() 的距离最大,其最大距离为BM sin60°=(BA1+A1M)sin60°=(a+
的距离最大,其最大距离为BM sin60°=(BA1+A1M)sin60°=(a+![]() a)·
a)·![]() =
=![]() a
a
试题3:数列{14-2n}的前n项和为Sn,数列{︱14-2n︱}的前n项和为Sn′,若Sn的最大值为Sm,则n≥m时,Sn′=
猜题理由:阅读理解能力是近几年高考试题的一种新要求,该题以等差数列为载体,考察了前n项和的性质,它运用了函数的观点。
详细解答:设an=14-2n,显然{an}为递减数列,所以前7项和最大,因此m=7,n≥7时,Sn′=S7+2·8-14+2·9-14+…+2n-14=42+(n-6)(n-7)。
试题4:求(2
cos![]() +1)tan
+1)tan![]() -2sin
-2sin![]() 的值
的值
猜题理由:三角公式已经大大减弱,纯粹的三角题难度不大,因此三角中常规的东西,如变角、降次,讲究角间的配合。化弦等方法正是三角中最重要的东西。我认为三角试题应体现原创性。
详细解答:原式=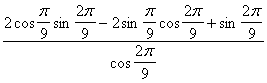 =
=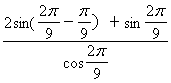 =
= =
=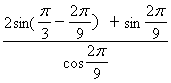 =
=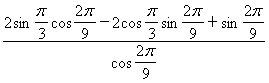 =
=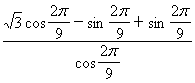 =
=![]()
试题5:设点P是双曲线![]() =1(a,b∈R+)上除顶点外的任意一点,F1、F2分别为左、右焦点,c为半焦距,△F1PF2的内切圆与边︱F1F2︱的切点为M,则︱F1M︱·︱MF2︱+︱OM︱2(O为坐标原点)的值是
=1(a,b∈R+)上除顶点外的任意一点,F1、F2分别为左、右焦点,c为半焦距,△F1PF2的内切圆与边︱F1F2︱的切点为M,则︱F1M︱·︱MF2︱+︱OM︱2(O为坐标原点)的值是
猜题理由:圆锥曲线定义的运用及深刻挖掘是解析几何试题的重要特征,它更能体现学生优良的数学思维品质。
详细解答:因为P是双曲线上一点,所以︱PF1︱-︱PF2︱=±2a等价于︱F1M︱-︱F2M︱=±2a,又︱F1M︱+︱F2M︱=2c,所以P在右支时,︱F1M︱=c+a,︱F2M︱=c-a,P在左支时,︱F1M︱=c-a,︱F2M︱=c+a,显然M点为双曲线顶点,∴︱OM︱2=a2,∴︱F1M︱·︱F2M︱+︱OM︱2=c2-a2+a2=c2
试题6:已知两个向量集合M={![]() ︱
︱![]() =(cos
=(cos![]() ,
,![]() ),
),![]() ∈R},N={
∈R},N={![]() ︱
︱![]() =(cos
=(cos![]() ,
,![]() +sin
+sin![]() )
)![]() ∈R},若M∩N≠
∈R},若M∩N≠![]() ,则
,则![]() 的取值范围是
的取值范围是
A.(-3,5] B.[,5] C.[2,5] D.[5,+∞)
猜题理由:平面向量作为新增内容,应该充分注意它与其它知识的联系,该题是集合、向量与三角知识的一个融汇,这应该是一个新的探索。
![]() 详细解答:由M∩N≠
详细解答:由M∩N≠![]() 知M、N中必有相同元素,设(cos
知M、N中必有相同元素,设(cos![]() ,
,![]() )=(cos
)=(cos![]() ,
,![]() +sin
+sin![]() ),则有 cos
),则有 cos![]() =cos
=cos![]()
![]() =
=![]() +sin
+sin![]() 消去
消去![]() 得
得![]() =4-cos2
=4-cos2![]() -sin
-sin![]()
=sin2![]() -sin
-sin![]() +3=(sin
+3=(sin![]() -)2+,sin
-)2+,sin![]() =时,
=时,![]() min=,当sin
min=,当sin![]() =-1时,
=-1时,![]() max=5,故选B。
max=5,故选B。
试题7:关于x的不等式(m2-m-2)x<cot m的解集为空集,则m的值为
A. 2 B.-1 C.-1或2 D.不存在这样的m
猜题理由:每年高考题几乎都有解不等式的试题,而给出了一个不等式的解集,去探索原不等式的性质,这给试题增加了思维度。
![]()
![]() 详细解答:不等式(m2-m-2)x<cot m的解集为空集当且仅当 (m2-m-2)=0
详细解答:不等式(m2-m-2)x<cot m的解集为空集当且仅当 (m2-m-2)=0
cot m<0
m=2或m=-1故选C。
试题8:设函数y=f(x)的反函数为f-1(x),将y=f(2x-3)的图像向左平移两个单位,再关于x轴对称后所得到的函数的反函数是( A )
A.
y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
猜题理由:反函数的概念在函数中占有重要位置,当给出一个具体解析式求反函数时几乎成了“定律”,但该题需要抽象出一般“算理”,这是学生的所缺乏的。
详细解答:将y=f(2x-3)向左平移两个单位,得到函数的解析式为y=f(2(x+2)-3)
=f(2x+1),关于x轴对称后所得到的函数![]()
![]() ∴x=
∴x=![]() 即 y=
即 y=![]() 。故选A。
。故选A。
试题9:设函数f(x)=x3,若0≤![]() ≤
≤![]() 时,f(m cos
时,f(m cos![]() )+f(1-m)>0恒成立,则实数m的取值范围是( )
)+f(1-m)>0恒成立,则实数m的取值范围是( )
A.
(0,1) B.(-∞,0) C. (-∞,1) D. (-∞,![]() )
)
猜题理由:小题综合化是当今高考试题的一种新要求。该题考察函数的增减性、奇偶性,解不等式及恒成立问题的处理方法,是一道综合性较强的试题。该题另一个特点思维量较大。
详细解答:显然f(x)是奇函数,又是R上的增函数,由f(m cos![]() )+f(1-m)>0得
)+f(1-m)>0得
f(m
cos![]() )> -f(1-m)即f(m
cos
)> -f(1-m)即f(m
cos![]() )> f(m-1)
)> f(m-1)![]() m cos
m cos![]() >m-1
>m-1 ![]() m cos
m cos![]() +(1-m)>0,令
+(1-m)>0,令![]() =cos
=cos![]() ,∵
,∵![]() ∈[0,
∈[0,![]() ],∴0≤
],∴0≤![]() ≤1,令f(
≤1,令f(![]() )=m
)=m![]() +(1-m),则f(m cos
+(1-m),则f(m cos![]() )+f(1-m)>0恒成立,当且仅当f(
)+f(1-m)>0恒成立,当且仅当f(![]() )>0(
)>0(![]() ∈[0,1])恒成立,当且仅当
∈[0,1])恒成立,当且仅当
|
f(1)>0 1-m>0
解法二:m=0时,有f(0)+f(1)=1>0成立,∴排除A、B。又m=![]() 时,f(
时,f(![]() cos
cos![]() )+f(
)+f(![]() )=
)=![]() cos3
cos3![]() +
+![]() =
=![]() (cos3
(cos3![]() +1)>0成立,排除D,因此选C。
+1)>0成立,排除D,因此选C。
试题10:M是抛物线y2=x上一点,N是圆(x+1)2+(y-1)2=1关于直线x-y+1=0的对称曲线上一点,则![]() 的最小值是( )
的最小值是( )
A.
![]() B.
B. ![]() C. 2+
C. 2+![]() D.
D. ![]()
猜题理由:直线与曲线、曲线与曲线的位置关系问题以及解析几何的最值问题是平面解析几何中两个重要问题,它们交织在一起构成一个综合试题,这也是高考试题的命题方向。
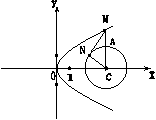 详细解答:圆(x+1)2+(y-4)2=1关于直线x-y+1=0
详细解答:圆(x+1)2+(y-4)2=1关于直线x-y+1=0
对称的曲线方程为c′:(x-3)2+y2=1如图,设M是y2=x
上一点,
![]() +
+![]() ≥
≥![]() =
=![]() +
+![]() ∴
∴![]() ≥
≥![]() ,∴只需
,∴只需
求圆心C到抛物线的最短距离,设M(y2,y),则![]() 2=(y2-3)2+y2=y4-5 y2+9=(y2-)2+9-=(y2-)2+∴y=±
2=(y2-3)2+y2=y4-5 y2+9=(y2-)2+9-=(y2-)2+∴y=±![]() 时,
时,![]() min=
min=![]() ,∴
,∴![]() min=
min=![]() -1
故选A。
-1
故选A。
2006高考数学预测
1、
在集合![]() 中任取一个元素,所取元素恰好满足方程
中任取一个元素,所取元素恰好满足方程![]() 的概率是
的概率是 ![]() 。
。
2、质地均匀的正方体木块的棱长为n,n为正整数且n≥2.在其表面涂上与材质颜色不同的蓝色后将木块分割成棱长为1的小正方体木块,假设从中任意取一块得到表面有蓝色的木块的概率为P,请研究P能否大于或小于![]() .
.
[解答]:当n=2时, P=1;
当n≥3时,有P=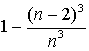 ,
,
P-![]() =
=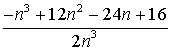 .
.
记y=g(x)=
![]() , x>2.
, x>2.
g′(x)=
![]() ,
,
可知在(2,+∞)上y= g(x)只有一个极大值点x=![]() ,
,
所以函数y= g(x)在(2, ![]() )上是增函数;在(
)上是增函数;在(![]() ,+∞)上是减函数.
,+∞)上是减函数.
又验证g(3)>0, g(9) >0, g(10)<0,
于是我们得到结论:当正整数2≤n≤9时, P>![]() ;当正整数n≥10时, P<
;当正整数n≥10时, P<![]() .
.
3.某一居民小区五幢住宅楼,由于有水紧缺,规定每一幢楼在一周内必须选择某一天停水(选择哪一天是等可能的)。假定每一楼之间的选择互不影响。
(1) 求个5幢楼均选择星期天停水的概率。
(2) 求至少有两幢选择同一天停水的概率。
(1)设5幢楼均选择星期天停水的事件为A,则
P(A)=![]() (6`)
(6`)
(2)设五幢楼选择的停电时间各不相同的事件为B,则
P(B)=![]() =
=![]() (12`)
(12`)
4、在正四棱锥S-ABCD中,E是BC的中点,P点在侧面![]() 内及其边界上运动,并且总是保持PE
内及其边界上运动,并且总是保持PE![]() AC.
AC.
(1)指出动点P的轨迹(即说明动点P在满足给定的条件下运动时所形成的图形),证明你的结论;
(2)以轨迹上的动点P为顶点的三棱锥P-CDE的最大体积是正四棱锥S-ABCD体积的几分之几?
(3)设动点P在G点的位置时三棱锥P-CDE的体积取最大值V1,二面角G-DE-C的大小为![]() ,二面角G-CE-D的大小为
,二面角G-CE-D的大小为![]() ,求
,求![]() 的值.
的值.
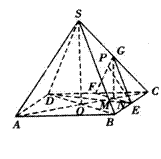 (4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其它条件不变,请指出点P的轨迹,证明你的结论.
(4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其它条件不变,请指出点P的轨迹,证明你的结论.
解析:(1)如图,分别取CD、SC的中点F、G,连结EF、EG、FG、BD.设AC与BD的交点为O,连结SO,则动点P的轨迹是![]() 的中位线FG.
的中位线FG.
由正四棱锥可得![]() .又
.又
![]()
![]() 平面EFG,
平面EFG,![]() 平面EFG,
平面EFG,![]() .
.
(2)由于![]() 是定值,所以当P到平面CDE的距离最大时,
是定值,所以当P到平面CDE的距离最大时,![]() 最大,易知当P与G重合时,P到平面CDE的距离最大,故
最大,易知当P与G重合时,P到平面CDE的距离最大,故![]() .又
.又![]() ,G到平面ABCD的距离是点S到平面ABCD的距离的
,G到平面ABCD的距离是点S到平面ABCD的距离的![]() ,
,
![]() .
.
(3)令![]() ,EF与AC交于N点,连结GN,则GN
,EF与AC交于N点,连结GN,则GN![]() 平面ABCD.
平面ABCD.
因此二面角G-DE-C和二面角G-CE-D的平面角的正切值的比就等于N到DE和CE的距离的倒数比.
![]() N是OC的中点,
N是OC的中点,![]() N到BC的距离为
N到BC的距离为![]() .
.
连结DE交OC于M,则M是![]() 的重心,
的重心,![]() .
.
又![]() ,
,
在![]() 中,容易求得N到DE的距离为
中,容易求得N到DE的距离为![]() .
.
故![]() .
.
(4)动点P在侧面SCD内部及其边界上运动,且总保持![]() ,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,
,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,![]() 平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E
平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E![]() //SB,E
//SB,E![]() //BD,分别交SC于
//BD,分别交SC于![]() ,交CD于
,交CD于![]() ,则平面E
,则平面E![]() //平面SBD,从而
//平面SBD,从而![]() 平面E
平面E![]() ,故点P的轨迹是线段
,故点P的轨迹是线段![]() .
.
说明:本题全方位地考查了立体几何中的主要内容,如线面与线线的位置关系、体积问题、二面角问题等.在立体几何的问题中给出了探求点的轨迹问题,与平面几何、解析几何紧密联系,体现了对综合运用知识的能力要求,考查的知识点丰富,具有相当的难度和深度,达到了压轴题的水平,是一道优秀的创新型试题.
5、已知![]() 是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求 AC 的取值范围.
(1)解:![]()
依题意![]() 在
在![]() 和[0,2]上有相反的单调性,
和[0,2]上有相反的单调性,
∴x = 0是f (x)的一个极值点,故![]() ,得c = 0
,得c = 0
(2)解:因为f (x)交x轴于点B(2,0)
∴![]() ,即
,即![]()
令![]() 得
得![]()
因为f (x)在[0,2]和[4,5]上有相反的单调性,∴![]() 在[0,2]和[4,5]上有相反的
在[0,2]和[4,5]上有相反的
符号
故2≤![]() ≤4 Þ -6≤
≤4 Þ -6≤![]() ≤-3
≤-3
假设存在点M(x0,y0)使得f (x)在点M的切线斜率为3b,则f / (x0) =3b,
即![]()
![]()
而-6≤![]() ≤-3,∴△<0
≤-3,∴△<0
故不存在点M(x0,y0),使得f (x)在点M的切线斜率为3b.
(3)解:设![]() ,依题意可令
,依题意可令![]()
![]()
则![]() 即
即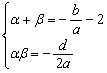
∴![]()
∵-6≤![]() ≤-3,∴当
≤-3,∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,故3≤ AC ≤4
,故3≤ AC ≤4![]()