保密★启用前　　　　　　　　　　　　　　　　　　　　　　　　　  试卷类型：A

中学学科网全国学科大联考2006年高考模拟试卷（一）

数学科试题(理科)　

命题人：王海平　　 审核人:王建宏  孟繁露

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、考场座位号、考试科目涂写在答题卡上．

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．不能答在试题卷上．

3.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至4页，第Ⅱ卷4至8页．共150分．考试时间120分钟．

第Ⅰ卷（选择题　共60分）

参考公式：

如果事件A、B互斥，那么P(A+B)=P(A)+P(B),　　　　　　　　　　　 

如果事件A、B相互独立，那么P(A·B)=P(A)·P(B),　　　　　　　　　

如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率.　　　　 

一、选择题：本大题共12小题，每小题5分，共60分.在每小题的四个选项中，有且只有一项是符合题目要求的.

1．设集合，定义P※Q＝，则P※Q中元素的个数为　　　　　　　　　　　　　　　　　　　　　  （　　）

　　　 A．3　　　　　　　　　　B．4　　　　　　　　　　C．7　　　　　　　　　　　 D．12

2．下列判断错误的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．命题“若q则p”与命题“若则”互为逆否命题

　　　 B．“am²<bm²”是“a<b”的充要条件

　　　 C．“矩形的两条对角线相等”的否命题为假

　　　 D．命题“”为真（其中为空集）

3．若复数（是虚数单位）是纯虚数，则实数的值为　　  （　 ）

A．2　　　　　  B．4　　　　　　　　  C．6　　　　　　 D．6

4．已知映射,其中A=B=R,对应法则,对于实数,在集合A中不存在原象,则的取值范围是　　　　　　　　　　　　　　　　　　  （　　）

 A．　　　　 B．　　　　　　 C．　　　　　  D．

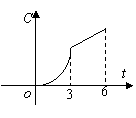
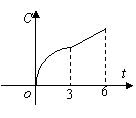
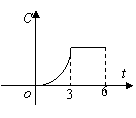
5．某工厂六年来生产某种产品的情况是：前三年年产量的增长速度越来越快，后三年年产量保持不变，则该厂六年来这种产品的可用图像表示的是　　　　　　　　　（　　）

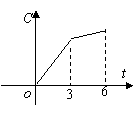   A.　　  　　　　　　B.　　　　　　　  　 C.　　　　　　　　  D.

6．已知函数f(x) =3 - 2x，g(x) = x²- 2x，构造函数F(x)，定义如下：当f(x)≥g(x)时，F(x) = g(x)；当f(x)＜g(x)时，F(x) =f(x)，那么F(x)　　　　　  　　　　　　　　　（ 　）

A．有最大值3，最小值-1 　　　　　 B．有最大值3，无最小值　　

C．有最大值7-2，无最小值　 　 D．无最大值，也无最小值

7．记二项式（1+2x）ⁿ展开式的各项系数和为a_n，其二项式系数和为b_n，则等于 　 （　　）　

　　　 A．1　　　　　　　　　　　　B．－1　　　　　　　　　　 C．0　　　　　　　　　　　　D．不存在

8．已知数列满足，，．若，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　 　　　　　　　　　 B．3　　　 　　　　　　　　　　 C．4　　　 　　　　　　　　　　 D．5

9．设函数满足，则方程根的个数可能是（　　）

A．无穷个　　　　  B．没有或者有限个　　C．有限个　　　D．没有或者无穷多　　　

10．将1，2，…，9这9个数平均分成三组，则每组的三个数都成等差数列的概率为（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　　D．

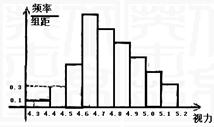11．为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，如右，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a, b的值分别为　 （　　）

　　A．0,27,78　　　　B．0,27,83　　　　C．2.7,78　　　　 D．2.7,83

12．已知函数，下面四个图象中的图象大致是　　　　　　　　　　　　　　　　（　　）

第Ⅱ卷（非选择题　共90分）

二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上）

13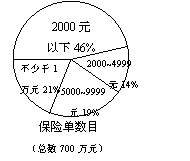．右图是某保险公司提供的资料，在1万元以上的保险单中，有少于2.5万元，那么不少于2.5万元的保险单有

　　　　　　　  万元．

14．已知项数为8的等比数列的中间两项是方程的两根，则数列的各项积是　　　　　 ．

15．某公司有5万元资金用于投资开发项目，如果成功，一年后可获利12%，一旦失败，一年后将丧失全部资金的50%，下表是过去200例类似项目开发的实施结果：

投资成功	投资失败
192次	8次

则该公司一年后估计可获收益的期望

是__________（元）．

16．已知n次式项式. 如果在一种算法中，计算的值需要k－1次乘法，计算P₃（x₀）的值共需要9次运算（6次乘法，3次加法），那么计算P₁₀（x₀）的值共需要　　　　　　  次运算.

下面给出一种减少运算次数的算法：P₀（x）=a₀，P_k+1（x）=xP_k（x）+a_k+1（k=0，1，2，…，n－1）.利用该算法，计算P₃（x₀）的值共需要6次运算，计算P₁₀（x₀）的值共需要　　　　次运算.

三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）

17．（本小题满分12分）某城市有甲、乙、丙3个旅游景点，一位客人游览这三个景点的概率分别是0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.

（Ⅰ）求ξ的分布及数学期望；

（Ⅱ）记“函数f(x)＝x²－3ξx＋1在区间[2，＋∞上单调递增”为事件A，求事件A的概率.

18．（本小题满分12分）设数列{a_n}和{b_n}满足a₁=b₁=6, a₂=b₂=4, a₃=b₃=3, 且数列{a_n+1－a_n }（n∈N*）是等差数列，数列{b_n－2}(n∈N*)是等比数列.

　 （Ⅰ）求数列{a_n}和{b_n}的通项公式；

　 （Ⅱ）是否存在k∈N*，使a_k－b_k∈（0，）？若存在，求出k；若不存在，说明理由.

19．（本小题满分12分）某企业有一条价值a万元的生产流水线，要提高该生产流水线的生产能力，提高产品的增加值，就要对流水线进行技术改造．假设增加值y万元与技改投入x万元之间的关系满足：
　　 ①y与成正比例；②当时，；③0≤≤t．其中t为常数且tÎ(0，2]．

(Ⅰ) 设，求出的表达式，并求其定义域；

(Ⅱ) 求出增加值y的最大值，并求出此时的x的值．

20．（本小题满分12分）已知函数

（Ⅰ）函数在区间（0，+）上是增函数还是减函数？证明你的结论；

（Ⅱ）若当时，恒成立，求正整数的最大值．

21．（本小题满分12分）设函数y＝f ( x )定义在R上, 对任意实数m , n恒有f ( m＋n )＝f ( m )·f ( n )，且当x＞0时, 0＜f ( x )＜1.

（Ⅰ）求证: f (0 )＝1；　　　　　 

（Ⅱ）求证: 当x＜0时, f ( x )＞1；

(Ⅲ) 求证: f ( x )在R上是减函数；

(Ⅳ) A＝{ (x , y ) f ( x ² )·f ( y ² )＞f (1) } , B＝{( x, y ) f ( ax－y＋2 )＝1, a∈R},

 若A∩B＝, 求a的取值范围.

22．（本小题满分14分）已知数列

（Ⅰ）证明

（Ⅱ）求数列的通项公式a_n.

中学学科网全国学科大联考2006年高考模拟试卷（一）

数学科试题(理科)详细答案　

命题人：王海平  审核人:王建宏　孟繁露

一、选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	B	C	A	A	C	B	B	D	B	A	C

二、填空题

13．91万元　

14．16　

15． 4760

16．次，次．

详细参考答案

一、选择题

1．解:  ∵P※Q＝，∴P※Q的元素有34＝12个，故选D．

2．解:用淘汰法验证可知“am²<bm²”是“a<b”的充分不必要条件，注意m=0的特殊情况，选B．

3．解法一：设，则，得：，，选C．

解法二：非零向量，满足是纯虚数的意即，这两个非零向量互相垂直．

根据题意得：，从而，选C．

说明：复数四则运算,复数为实数、纯虚数的充要条件,复数的模作为复数内容的重点．

4．解：可以判定对应法则是从A到C的函数（，且是该函数的值域），于是对于实数,在集合A中不存在原象,则的取值范围构成集合，注意到，故，．

从而答案为A．

5．解：前三年年产量的增长速度越来越快，总产量C与时间t（年）的函数关系，在图上反映出来，当时是选项A、C中的形状；又后三年年产量保持不变，总产量C与时间t（年）的函数关系应如选项A所示,于是选A.

说明：本题很容易错选C，这是由于没有看清题中函数关系是总产量C与的时间t（年），而不是年产量C与的时间t（年）的函数关系．

6．解：选C． 利用图象法求之．其中F(x)= ．

7．解：由题意得_， ，于是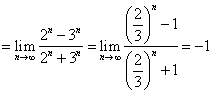，因此，选B

8．解法一：特殊值法，当时，

　　　　　　　 由此可推测，故选B．

解法二：∵，∴，，

　　　 ∴是以（）为首项，以为公比6的等比数列，

令，则

…

　　 …

　　

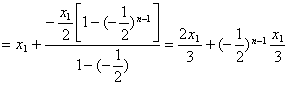
∴，∴，故选B.

解法三：∵，∴，

　　　　∴其特征方程为，

　　　　　　　解得　　　 ，，

　　　　　　　　　　　　　 ，

　　　　 ∵，，∴，，

　　　　 ∴，以下同解法二．

9．解：当时，满足条件，此时方程根有无数个，故B、C错

　　　　当时，也满足条件，此时方程没有根，故A错

选D．

10．本题主要考查平均分组问题及概率问题.

解：将1，2，3，---，9平均分成三组的数目为,又每组的三个数成等差数列的种数为4，选B．

说明：这是一道概率题，属于等可能事件，在求的过程中，先求出不加条件限制的所有可能性a，然后再根据条件，求出满足题目要求的可能种数b，最后要求的概率就是．

11．本题涉及数理统计的若干知识．

解：由图象可知，前4组的公比为3，最大频率，设后六组公差为，则，解得：，

后四组公差为－0.05， 所以，视力在4.6到5.0之间的学生数为（0.27＋0.22＋0.17＋0.12）×100＝78（人）,选A．

说明：本题是一道数理统计图象题,关于统计一般可分为三步,第一步抽样,第二步根据抽样所得结果,画成图形,第三步根据图形,分析结论.本题是统计的第二步,在此类问题中,可画成两种图形,一个是频率分布直方图,另一个是频率分布条形图,两者有很大的不同,前者是以面积表示频数,频率分布条形图是以高度表示频数.

12．本题考查导函数的图象及其性质,由图象得，从而导出是函数f(x)极值点是解本题的关健．

解：由图象知，，所以是函数的极值点，又因为在上，，在上，，因此在上，单调递减，故选C．

说明：要注意,若是函数y=f(x)的极值点,则有,但是若,则是不一定是函数y=f(x)极值点,所以要判断一个点是否为极值点,还要检验点的两侧的单调性是否不同．

二、填空题

13.解:不少于1万元的占700万元的21%，为700×21%=147万元．

1万元以上的保单中，超过或等于2.5万元的保单占，

金额为×147=91万元，故不少于2.5万元的保险单有91万元．

14. 解：由等比数列性质知，故各项的积是16．

15．解：投资成功的概率是，失败的概率是，所以所求的数学期望应该是：
故答案为：4760．

16．解：由题意知道的值需要次运算,即进行次的乘法运算可得到的结果，对于这里进行了3次运算,

　　　 进行了2次运算,进行1次运算,最后之间的加法运算进行了3次这样总共进行了次运算

对于总共进行了次

乘法运算及次加法运算所总共进行了次

由改进算法可知：

　　　 ,,，运算次数从后往前算和为：次

说明：本题目属于信息题,做此类题需要认真分析题目本身所给的信息.

三、解答题

17．解：（I）分别记“客人游览甲景点”，“客人游览乙景点”，“客人游览丙景点”

　　　 为事件A₁，A₂，A₃. 由已知A₁，A₂，A₃相互独立，P（A₁）=0.4，P（A₂）=0.5，

　　　 P（A₃）=0.6.

　　　 客人游览的景点数的可能取值为0，1，2，3. 相应地，客人没有游览的景点数的可能取

　　　 值为3，2，1，0，所以的可能取值为1，3.

　　　 P（=3）=P（A₁·A₂·A₃）+ P（）

= P（A₁）P（A₂）P（A₃）+P（）

=2×0.4×0.5×0.6=0.24，

1　　 3　 P 0.76 0.24 ………………6分

　　　 P（=1）=1－0.24=0.76.

　　　 所以的分布列为

　　　 E=1×0.76+3×0.24=1.48. 

（Ⅱ）解法一  因为

所以函数上单调递增，

要使上单调递增，当且仅当

从而………………12分

解法二：的可能取值为1，3.

当=1时，函数上单调递增，

当=3时，函数上不单调递增.0

所以　　　 　　………………12分

18．解：（I）由已知a₂－a₁=－2, a₃－a₂=－1, －1－(－2)=1　

　　　　　　　　  ∴a_n+1－a_n=(a₂－a₁)+(n－1)·1=n－3　

n≥2时，a_n=( a_n－a_n－1)+( a_n－1－a_n－2)+…+( a₃－a₂)+( a₂－a₁)+ a₁

　　　　  =(n－4)+(n－5) +…+(－1)+(－2)+6

　　　　  =，对n=1也合适.

 ∴a_n=　(n∈N*)　　　　　　 ……………………3分

又b₁－2=4、b₂－2=2 .而　∴b_n－2=（b₁－2）·()^n－1即b_n=2+8·()ⁿ …6分

∴数列{a_n}、{b_n}的通项公式分别为：a_n= ，　b_n=2+()^n－3

（II）设

当k≥4时为k的增函数，－8·()^k也为k的增函数，而f(4)=

∴当k≥4时a^k－b^k≥　　　　　　　　　　  ………………10分

又f(1)=f(2)=f(3)=0， ∴不存在k，使f(k)∈（0，）…………12分

19．解：（Ⅰ）设，∵当时，，∴
∴．从而有．　　　　　　  …………3分
∵0≤≤t，得0≤x≤．
∴（0≤x≤）．　　　　…………6分

(Ⅱ）∵，∴．
令，得x=0，．

（1）当≥，即当1≤t≤2时，
若，>0，由于在上连续，∴在上为增函数；若，<0，在上为减函数．
∴对于1≤t≤2的情况，当时，f (x)的最大值为．……9分

（2）当，即当0≤t≤1时，仿（1）得在上是增函数，
∴对于0≤t≤1的情况，当时，f (x)的最大值是．

…………11分

综上可知：当1≤t≤2时，增加值y的最大值是，此时技改投入为．
当0≤t≤1时，增加值y的最大值是，此时技改投入为．

…………12分

说明：本题属经济类应用题，是近年高考的热点与重点，主要考查函数、导数的知识及运用这些知识解决问题的能力．

20．解：（Ⅰ）

　 .

　 因此函数在区间（0，+∞）上是减函数．　　　　　　　　　　  ……6分

（Ⅱ）解法一：当时，恒成立，令有

又为正整数. 的最大值不大于3.　　　　　　　　　　　　　  ……8分

下面证明当恒成立.

即证当时，恒成立.

令

当

取得最小值

时，恒成立，因此正整数的最大值为3.

……12分

（Ⅱ）解法二：当时，恒成立，

即恒成立.

即的最小值大于

上连续递增，

又

存在唯一实根，且满足：

由知：

的最小值为

因此正整数的最大值为3.　　　　　　　　　　　　　　　　　　  ……12分

说明：本题体现出在研究函数的单调性等性质时，用初等方法往往技巧性要求较高（有时甚至不能求解），而导数方法显得简捷方便．因此，在研究函数性质时，要优先考虑使用求导的方法．

21．解: (Ⅰ)令

时, 　　　　　　…………………2分

(Ⅱ) 时, ,

又,　

, .　　　　　　　　　　　　　　　　　 …………………4分

(Ⅲ)设,

　 　　　　　　　　　　　　　　　…………………6分

又均有,

　　　　　　　　　　　　　　　　　  …………………7分　

在R上为单调减函数. 　　　　　　　　　　　　　　　…………………8分

(Ⅳ) 　　　　　　　 …………………9分

在R上为单调减函数, 　　　　　　　 …………………10分

又

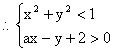, 无解(即无交点).　　　　  

圆心到直线的距离大于等于1,

有: ,　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　 …………………12分

22．本题考查数列的基础知识，考查运算能力和推理能力.第（1）问是证明递推关系，联想到用数学归纳法，第（2）问是计算题，也必须通过递推关系进行分析求解.

解：（Ⅰ）方法一 用数学归纳法证明：

1°当n=1时，

　 ∴，命题正确.

2°假设n=k时有

　 则

　

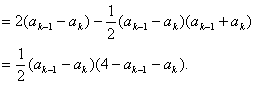
而

又

∴时命题正确.

由1°、2°知，对一切n∈N时有　　　　　　　　  ……6分

方法二：用数学归纳法证明：

　　　 1°当n=1时，∴；

　　2°假设n=k时有成立，

　　　 令，在[0，2]上单调递增，所以由假设

有：即

也即当n=k+1时　成立，所以对一切 ……6分

　 （Ⅱ）下面来求数列的通项：

所以

,

又b_n=－1，所以.　　　　　  ……14分

说明：数列是高考考纲中明文规定必考内容之一,必须理解数列的概念,了解数列通项公式的意义,了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.数列与不等式的给合往往得高考数学的热点之一,也成为诸多省份的最后压轴大题,解决此类问题,必须有过硬的数学基础知识与过人的数学技巧,同时运用数学归纳法也是比较好的选择,不过在使用数学归纳法的过程中,一定要遵循数学归纳法的步骤.